З шкільного курсу математики відомо, що однією з найважливіших задач природознавства є вивчення змінних величин, тобто таких, які можуть приймати будь які значення з деякої множини. Зустрічалися також з поняттям функціональної залежності змінної величини  від іншої змінної величини
від іншої змінної величини  :
:
 .
.
Якщо величина  змінюється, то відповідним чином, взагалі кажучи, буде змінюватися і величина
змінюється, то відповідним чином, взагалі кажучи, буде змінюватися і величина  .
.
Нехай, наприклад,  . Легко знайти, що, якщо
. Легко знайти, що, якщо  приймає значення, наприклад, -2, -1, 0, 1, 2, то
приймає значення, наприклад, -2, -1, 0, 1, 2, то  відповідно прийме значення 4, 1, 0, 1, 4.
відповідно прийме значення 4, 1, 0, 1, 4.
Припустимо тепер, що змінна  приймає значення, які наближаються до деякої заданої величини. І поставимо питання: до якої величини будуть наближатися відповідні значення величини
приймає значення, які наближаються до деякої заданої величини. І поставимо питання: до якої величини будуть наближатися відповідні значення величини  ?
?
На перший погляд ця задача розв’язується дуже просто. Нехай у випадку з функцією  значення
значення  наближаються до числа 1. Тоді легко підрахувати, що і значення
наближаються до числа 1. Тоді легко підрахувати, що і значення  також будуть наближатися до числа 1. Наприклад:
також будуть наближатися до числа 1. Наприклад:

|
| 0,5
| 0,75
| 0,9
| 0,95
| 0,99
|

|
| 0,25
| 0,5625
| 0,81
| 0,9025
| 0,9801
|
Те, що значення  будуть наближатися, або, як кажуть у математиці, прямувати до числа 1, здавалося би можна легко встановити, якщо у рівності
будуть наближатися, або, як кажуть у математиці, прямувати до числа 1, здавалося би можна легко встановити, якщо у рівності  покласти
покласти  . Але такий “метод” справджується далеко не завжди. Розглянемо функцію:
. Але такий “метод” справджується далеко не завжди. Розглянемо функцію:
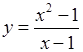 .
.
І знову поставимо те ж саме питання: до якого значення буде прямувати  , якщо
, якщо  прямує до 1?
прямує до 1?
У даній ситуації ми не можемо просто покласти  , оскільки отримаємо беззмістовний вираз:
, оскільки отримаємо беззмістовний вираз:
 .
.
Але ми ставимо питання не про обчислення значення  при
при  (цього значення взагалі не існує), а про знаходження величини, до якої прямує
(цього значення взагалі не існує), а про знаходження величини, до якої прямує  , якщо
, якщо  тільки прямує до 1 (але не дорівнює 1). А оскільки
тільки прямує до 1 (але не дорівнює 1). А оскільки 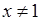 , тобто
, тобто 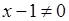 , то скориставшись формулою
, то скориставшись формулою 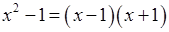 , і, скоротивши на
, і, скоротивши на  , отримаємо, що для всіх
, отримаємо, що для всіх 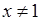 виконано:
виконано:
 .
.
А тоді легко бачити, що при прямуванні  до 1 величина
до 1 величина  прямує до 1+1=2.
прямує до 1+1=2.
Таким чином ми бачимо, що питання про те, до якого значення прямує величина  , якщо
, якщо  прямує до деякої заданої величини
прямує до деякої заданої величини  , можна розв’язувати навіть у тому випадку, коли
, можна розв’язувати навіть у тому випадку, коли  не визначена у точці
не визначена у точці  . Таке значення у математиці називають границею функції
. Таке значення у математиці називають границею функції  при прямуванні
при прямуванні  до
до  .
.
Зауважимо, що навіть у тому випадку, коли функція  визначена у точці
визначена у точці  , її границя у точці
, її границя у точці  не завжди співпадає зі значенням функції у цій точці. Нехай наприклад:
не завжди співпадає зі значенням функції у цій точці. Нехай наприклад:
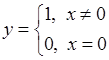
Нижче ми покажемо, що границя функції  при прямуванні
при прямуванні  до 0 дорівнює 1. В той же час значення функції
до 0 дорівнює 1. В той же час значення функції  при
при  дорівнює 0.
дорівнює 0.
Не завжди границя існує. Наприклад функція 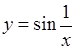 , як буде встановлено пізніше, не має границі при прямуванні
, як буде встановлено пізніше, не має границі при прямуванні  до 0.
до 0.
З необхідністю обчислювати граничні значення різних величин людство зіткнулося ще у давнині. В стародавні часи люди вміли обчислювати площі простіших геометричних фігур – прямокутників, трикутників. Але довгий час залишалося нерозв’язаним питання про знаходження площі круга заданого радіуса, оскільки воно було пов’язане з трансцендентним числом  . І цю задачу розв’язували наступним чином: в круг вписували правильний многокутник, потім розбивали його на конгруентні рівнобедрені трикутники (рис. 14). Вміючи знайти площу
. І цю задачу розв’язували наступним чином: в круг вписували правильний многокутник, потім розбивали його на конгруентні рівнобедрені трикутники (рис. 14). Вміючи знайти площу  кожного з них (
кожного з них (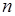 – число сторін многокутника), наближено покладали:
– число сторін многокутника), наближено покладали:
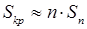 . (8.1)
. (8.1)
Наскільки точна ця формула? Вона тим точніша, чим більше 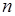 , тобто чим менше площа многокутника відрізняється від площі круга. Обираючи все більші та більші значення
, тобто чим менше площа многокутника відрізняється від площі круга. Обираючи все більші та більші значення 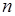 , ми будемо отримувати все більш точні значення площі круга.
, ми будемо отримувати все більш точні значення площі круга.

Рис. 14.
Але, скільки б ми не збільшували 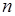 у формулі (8.1), точної формули ми все ж таки не отримаємо. А як отримати точне значення площі? Для цього треба знайти границю величини
у формулі (8.1), точної формули ми все ж таки не отримаємо. А як отримати точне значення площі? Для цього треба знайти границю величини 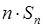 , якщо
, якщо 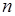 прямує до нескінченності. Тобто знайти границю площ вписаних многокутників при необмеженому збільшенні числа їх сторін. Ця границя, як ми покажемо в п. 27, дорівнює
прямує до нескінченності. Тобто знайти границю площ вписаних многокутників при необмеженому збільшенні числа їх сторін. Ця границя, як ми покажемо в п. 27, дорівнює  , де
, де  – радіус круга. Це й є точна формула для площі круга.
– радіус круга. Це й є точна формула для площі круга.
Необхідність обчислення граничних значень величин виникає також і в задачах механіки та фізики. Нехай ми маємо точку 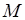 , яка рухається вздовж прямої. Нехай за час
, яка рухається вздовж прямої. Нехай за час  ця точка пройшла відстань
ця точка пройшла відстань 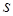 . Відомо, що середня швидкість руху на цій ділянці шляху обчислюється за формулою:
. Відомо, що середня швидкість руху на цій ділянці шляху обчислюється за формулою:
 .
.
Але це саме середня швидкість. Разом з цим на протязі часу  точка
точка 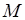 може рухатися нерівномірно: спочатку, наприклад, швидко, потім повільно, а певний час взагалі стояти на одному місці, потім знову швидко (приблизно так відбувається рух транспорту по міським вулицям). Таким чином середня швидкість не є достатньо адекватною характеристикою руху. Тому часто виникає задача знаходження швидкості не на протязі якогось проміжку часу, а в будь який момент часу, тобто так званої миттєвої швидкості. Як її можна знайти? Як границю значення середньої швидкості
може рухатися нерівномірно: спочатку, наприклад, швидко, потім повільно, а певний час взагалі стояти на одному місці, потім знову швидко (приблизно так відбувається рух транспорту по міським вулицям). Таким чином середня швидкість не є достатньо адекватною характеристикою руху. Тому часто виникає задача знаходження швидкості не на протязі якогось проміжку часу, а в будь який момент часу, тобто так званої миттєвої швидкості. Як її можна знайти? Як границю значення середньої швидкості 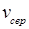 при прямуванні проміжку часу
при прямуванні проміжку часу  до нуля. Відмітимо також, що ця задача водночас приводить до одного з найважливіших понять математиці – поняття похідної (див. розділ “Диференціальне числення функції однієї змінної”).
до нуля. Відмітимо також, що ця задача водночас приводить до одного з найважливіших понять математиці – поняття похідної (див. розділ “Диференціальне числення функції однієї змінної”).
Вивчення границь ми почнемо з одного з простіших випадків – границі числової послідовності.
Означення. Якщо кожному натуральному числу 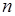 за певним законом поставлено у відповідність одне й тільки одне дійсне число
за певним законом поставлено у відповідність одне й тільки одне дійсне число  , то множину чисел
, то множину чисел  називають числовою послідовністю (або просто послідовністю).
називають числовою послідовністю (або просто послідовністю).
Іншими словами послідовність – це зліченна занумерована сукупність дійсних чисел.
Простіші приклади послідовностей зустрічаються вже у шкільному курсі алгебри та початків аналізу. Наприклад, множина натуральних чисел  утворює послідовність – тут кожному натуральному числу
утворює послідовність – тут кожному натуральному числу 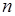 поставлено у відповідність саме це число. Іншими прикладами є арифметична
поставлено у відповідність саме це число. Іншими прикладами є арифметична  та геометрична
та геометрична  прогресії.
прогресії.
Вираз  називається загальним членом послідовності. Це формула, яка за будь яким натуральним числом
називається загальним членом послідовності. Це формула, яка за будь яким натуральним числом 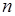 дозволяє знайти елемент послідовності з номером
дозволяє знайти елемент послідовності з номером 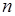 . Наприклад, для послідовності натуральних чисел
. Наприклад, для послідовності натуральних чисел  , для арифметичної прогресії
, для арифметичної прогресії  , а для геометричної
, а для геометричної  .
.
Наведемо ще кілька прикладів послідовностей та їх загальних членів.
1)  ,
,
2)  ,
,
3)  ,
,
4)  ,
,
5) 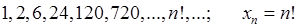 .
.
Нагадаємо тут, що  (
(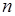 -факторіал) – це добуток всіх натуральних чисел від 1 до
-факторіал) – це добуток всіх натуральних чисел від 1 до 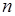 , тобто
, тобто  .
.
Числові послідовності можна задавати і так званим рекурентним (від лат. recurrens – зворотний) способом. Суть його у тому, що задаються декілька (наприклад 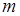 ) перших членів послідовності і вказується правило, за яким за відомими послідовними
) перших членів послідовності і вказується правило, за яким за відомими послідовними 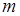 членами послідовності можна знайти наступний член. Наприклад відомі у математиці числа Фібоначчі визначаються так:
членами послідовності можна знайти наступний член. Наприклад відомі у математиці числа Фібоначчі визначаються так:
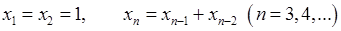
Тобто кожне число, починаючи з третього, дорівнює сумі двох попередніх.
Іноді за рекурентною формулою вдається знайти і загальний член послідовності, але не завжди це можливо. Відповідні задачі розглядаються у такій галузі математики, як теорія різницевих рівнянь.
У подальшому послідовність, що має загальний член  , будемо записувати так:
, будемо записувати так: 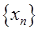 .
.
Означення. Послідовність 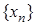 називається обмеженою зверху, якщо існує число
називається обмеженою зверху, якщо існує число  таке, що
таке, що  виконано:
виконано: 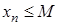 .
.
Означення. Послідовність 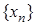 називається обмеженою знизу, якщо існує число
називається обмеженою знизу, якщо існує число  таке, що
таке, що  виконано:
виконано:  .
.
Означення. Послідовність 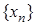 називається обмеженою, якщо вона обмежена і зверху і знизу.
називається обмеженою, якщо вона обмежена і зверху і знизу.
Таким чином, послідовність обмежена, якщо обмежена множина її елементів. Для обмеженої послідовності маємо:  таке, що
таке, що  виконано:
виконано: 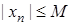 .
.
Наприклад, послідовність  обмежена зверху (але не обмежена знизу), послідовність
обмежена зверху (але не обмежена знизу), послідовність  обмежена знизу (але не обмежена зверху), а послідовність
обмежена знизу (але не обмежена зверху), а послідовність  обмежена.
обмежена.
Означення. Послідовність 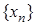 називається зростаючою (неспадною), якщо
називається зростаючою (неспадною), якщо  виконано:
виконано:  (
(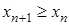 ).
).
Тобто кожен член послідовності, починаючи з другого, більше (не менше) попереднього.
Означення. Послідовність 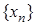 називається спадною (незростаючою), якщо
називається спадною (незростаючою), якщо  виконано:
виконано:  (
( ).
).
Тобто кожен член послідовності, починаючи з другого, менше (не більше) попереднього.
Наприклад, послідовність 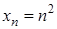 – зростаюча, послідовність
– зростаюча, послідовність 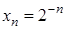 – спадна, послідовність
– спадна, послідовність 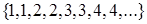 – неспадна, послідовність
– неспадна, послідовність  – незростаюча.
– незростаюча.
Зростаючі, спадні, незростаючі та неспадні послідовност називаються монотонними послідовностями.
Означення. Сумою послідовностей 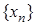 та
та 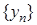 називається послідовність
називається послідовність  (кожен член цієї послідовності дорівнює сумі відповідних членів послідовностей
(кожен член цієї послідовності дорівнює сумі відповідних членів послідовностей 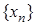 та
та 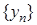 ).
).
Аналогічним чином визначаються різниця, добуток і частка послідовностей.
Границя послідовності.
Перейдемо тепер безпосередньо до поняття границі послідовності. Розглянемо послідовність  . Відмітимо на числовій прямій точки, які відповідають декілька першим членам цієї послідовності.
. Відмітимо на числовій прямій точки, які відповідають декілька першим членам цієї послідовності.
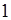

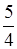

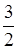
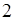
Рис. 15.
Ми бачимо, що зі зростанням номера 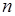 елементи послідовності наближаються до числа 1. Розглянемо інтервал
елементи послідовності наближаються до числа 1. Розглянемо інтервал  числової осі, який містить точку 1. Цей інтервал є 0,2–околом точки 1, і
числової осі, який містить точку 1. Цей інтервал є 0,2–околом точки 1, і 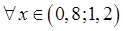 виконана нерівність
виконана нерівність 
Тепер дослідимо уважніше характер наближення елементів нашої послідовності до числа 1. Очевидно, що перші 5 членів послідовності 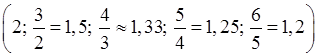 не належать вказаному інтервалу (нагадаємо, що межа 1,2 інтервалу цьому інтервалу не належить). А вся решта елементів, починаючи з шостого
не належать вказаному інтервалу (нагадаємо, що межа 1,2 інтервалу цьому інтервалу не належить). А вся решта елементів, починаючи з шостого  , опиняються всередині його, отже для них буде виконано нерівність:
, опиняються всередині його, отже для них буде виконано нерівність:

Ми можемо сказати, що для числа 0,2 знайшовся номер  такий, що, починаючи з наступного за ним, тобто
такий, що, починаючи з наступного за ним, тобто  , всі елементи послідовності будуть задовольняти нерівність (8.2).
, всі елементи послідовності будуть задовольняти нерівність (8.2).
Тепер розглянемо інший, більш вузький окіл точки 1, а саме  , тобто 0,1–окіл точки 1. І для цього околу спостерігається ситуація, аналогічна попередній. Цього разу перші 10 елементів нашої послідовності
, тобто 0,1–окіл точки 1. І для цього околу спостерігається ситуація, аналогічна попередній. Цього разу перші 10 елементів нашої послідовності 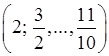 вказаному околу не належать, а решта, починаючи з 11-го
вказаному околу не належать, а решта, починаючи з 11-го 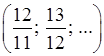 , належать, і для них виконано нерівність
, належать, і для них виконано нерівність
 .
.
Аналогічно, якщо ми розглянемо, наприклад, 0,01–окіл точки 1, тобто множину точок  , що задовольняє нерівність
, що задовольняє нерівність  , то помітимо, що, починаючи з номера, наступного за
, то помітимо, що, починаючи з номера, наступного за  , всі елементи послідовності
, всі елементи послідовності 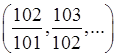 потрапляють всередину цього околу, а за його межами залишається лише скінчена кількість елементів послідовності
потрапляють всередину цього околу, а за його межами залишається лише скінчена кількість елементів послідовності  , тобто буде виконано нерівність
, тобто буде виконано нерівність 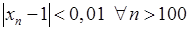 .
.
Тепер можна помітити деяку закономірність. Як би ми не звужували окіл точки  , завжди знайдеться такий номер
, завжди знайдеться такий номер  такий, що починаючи з наступного за ним, всі елементи послідовності потраплять всередину цього околу (тобто нескінченна їх кількість), а за його межами буде міститися лише скінчена кількість елементів послідовності. У першому з розглянутих випадків номер
такий, що починаючи з наступного за ним, всі елементи послідовності потраплять всередину цього околу (тобто нескінченна їх кількість), а за його межами буде міститися лише скінчена кількість елементів послідовності. У першому з розглянутих випадків номер  дорівнював 5, у другому 10, у третьому 100. Від чого він залежить? Очевидно від довжини нашого околу – чим вужчим становився окіл, тім, взагалі кажучи, був більшим номер
дорівнював 5, у другому 10, у третьому 100. Від чого він залежить? Очевидно від довжини нашого околу – чим вужчим становився окіл, тім, взагалі кажучи, був більшим номер  . Не будемо тепер точно фіксувати довжину околу, а припустимо, що його довжина дорівнює
. Не будемо тепер точно фіксувати довжину околу, а припустимо, що його довжина дорівнює  , де
, де 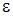 – мале додатне число, тобто розглянемо
– мале додатне число, тобто розглянемо 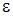 -окіл точки
-окіл точки  . Для всіх
. Для всіх  з цього околу виконано нерівність:
з цього околу виконано нерівність:
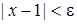 .
.
Тепер можна встановити такий факт: починаючи з номера, наступного за  (тут
(тут 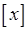 – ціла частина числа
– ціла частина числа  ) всі елементи послідовності
) всі елементи послідовності  будуть належати інтервалу
будуть належати інтервалу  . Таким чином, номер
. Таким чином, номер  , взагалі кажучи, залежить від числа
, взагалі кажучи, залежить від числа 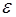 , який визначає довжину інтервалу. Тобто встановили наступне:
, який визначає довжину інтервалу. Тобто встановили наступне:
 (тобто
(тобто  , що залежить від
, що залежить від 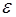 ) такий, що
) такий, що  виконана нерівність:
виконана нерівність:
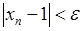 .
.
У цьому випадку кажуть, що число 1 є границею послідовності 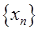 при
при 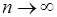 , і пишуть:
, і пишуть:
 .
.
( – скорочення від limes – границя).
– скорочення від limes – границя).
А тепер ми можемо сформулювати означення границі послідовності у загальному випадку:
Означення. Число  називається границею послідовності
називається границею послідовності 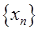 , якщо для будь якого додатного числа
, якщо для будь якого додатного числа 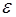 знайдеться такий номер
знайдеться такий номер  , який залежить від
, який залежить від 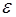 , що для всіх номерів
, що для всіх номерів 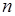 , більших, ніж
, більших, ніж  , виконується нерівність:
, виконується нерівність:
 .
.
За допомогою кванторів це означення записується так:
Число  називається границею послідовності
називається границею послідовності 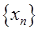 , якщо
, якщо
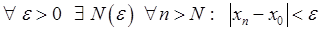 .
.
(як бачимо, за допомогою кванторів значно коротше).
У цьому випадку ми пишемо:
 .
.
Іншими словами, це означає, що у будь якому, скільки завгодно малому околі точки  знайдеться нескінченна кількість елементів послідовності, а за межами цього околу залишається лише скінченна їх кількість.
знайдеться нескінченна кількість елементів послідовності, а за межами цього околу залишається лише скінченна їх кількість.
Приклади.
1. Розглянемо сталу послідовність, тобто 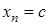 . Покажемо, що
. Покажемо, що  . Задамо довільне
. Задамо довільне  . Очевидно, що нерівність
. Очевидно, що нерівність 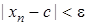 виконується для будь якого
виконується для будь якого  , отже у якості
, отже у якості 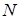 можна взяти 1.
можна взяти 1.
2. Довести, що 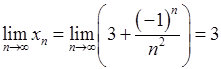 .
.
Задамо довільне 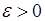 і розглянемо:
і розглянемо:
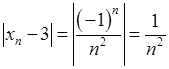 .
.
Будемо вимагати, щоб виконувалась нерівність:
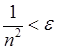 .
.
Тоді  , або
, або  . Отже, якщо
. Отже, якщо 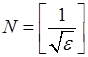 , то для всіх елемен-
, то для всіх елемен-
тів послідовності, починаючи з  , буде виконано:
, буде виконано:  . Таким чином,
. Таким чином, 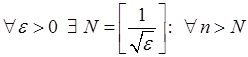 виконано
виконано  . Це й означає, що
. Це й означає, що 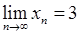 .
.
3. Довести, що  .
.
Задамо довільне 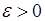 і розглянемо:
і розглянемо:
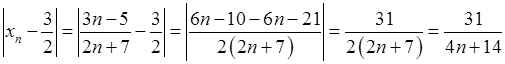 .
.
Якщо вимагати, щоб  , то
, то  . Таким чином, якщо
. Таким чином, якщо  , то, починаючи з номера
, то, починаючи з номера  , буде виконано нерівність
, буде виконано нерівність  . Отже
. Отже 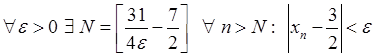 , що й треба було довести.
, що й треба було довести.
4. Доведемо, що послідовність  не має ніякої
не має ніякої
границі.
Загальний член цієї послідовності  . Припустимо, що існує
. Припустимо, що існує  . Тоді
. Тоді 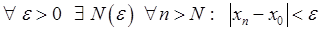 . Оберемо, наприклад
. Оберемо, наприклад  . Тоді, починаючи з номера
. Тоді, починаючи з номера  , буде виконано:
, буде виконано:
 .
.
Розглянемо деякий номер  . Тоді
. Тоді  , оскільки будь які два сусідні члени послідовності відрізняються на 2. З іншого боку:
, оскільки будь які два сусідні члени послідовності відрізняються на 2. З іншого боку:
 .
.
Таким чином отримали невірну нерівність  . Це й показує, що у даної послідовності не існує границі.
. Це й показує, що у даної послідовності не існує границі.
Можуть бути такі послідовності, які мають границю, але ця границя нескінченна.
Означення. Якщо  такий, що
такий, що 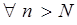 виконано нерівність
виконано нерівність  , то кажуть, що
, то кажуть, що  .
.
Тобто за рахунок збільшення номера 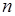 модуль елемента
модуль елемента  послідовності можна зробити більшим, ніж будь яке наперед задане число
послідовності можна зробити більшим, ніж будь яке наперед задане число 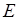 .
.
Приклад. Довести, що  .
.
Задамо довільне 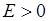 і розглянемо нерівність:
і розглянемо нерівність:
 .
.
Ця нерівність завжди буде виконана, якщо  , або
, або  .
.
Аналогічно вводяться для послідовності 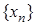 нескінченні границі, які дорівнюють
нескінченні границі, які дорівнюють 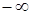 та
та  . Вони визначаються так:
. Вони визначаються так:
Означення. Якщо  такий, що
такий, що 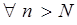 виконано нерівність
виконано нерівність  , то кажуть, що
, то кажуть, що 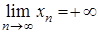 .
.
Означення. Якщо  такий, що
такий, що 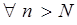 виконано нерівність
виконано нерівність  , то кажуть, що
, то кажуть, що  .
.
Означення. Якщо послідовність має скінченну границю, то вона називається збіжною, у протилежному випадку – розбіжною.
Наприклад, послідовності  ,
, 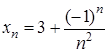 – збіжні, а послідовності
– збіжні, а послідовності  ,
, 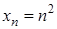 ,
,  ,
,  – розбіжні.
– розбіжні.


 від іншої змінної величини
від іншої змінної величини  :
: .
. . Легко знайти, що, якщо
. Легко знайти, що, якщо  . Але такий “метод” справджується далеко не завжди. Розглянемо функцію:
. Але такий “метод” справджується далеко не завжди. Розглянемо функцію: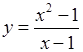 .
. .
.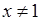 , тобто
, тобто 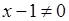 , то скориставшись формулою
, то скориставшись формулою 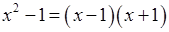 , і, скоротивши на
, і, скоротивши на  , отримаємо, що для всіх
, отримаємо, що для всіх  .
. , можна розв’язувати навіть у тому випадку, коли
, можна розв’язувати навіть у тому випадку, коли 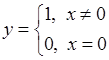
 дорівнює 0.
дорівнює 0.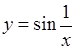 , як буде встановлено пізніше, не має границі при прямуванні
, як буде встановлено пізніше, не має границі при прямуванні  . І цю задачу розв’язували наступним чином: в круг вписували правильний многокутник, потім розбивали його на конгруентні рівнобедрені трикутники (рис. 14). Вміючи знайти площу
. І цю задачу розв’язували наступним чином: в круг вписували правильний многокутник, потім розбивали його на конгруентні рівнобедрені трикутники (рис. 14). Вміючи знайти площу  кожного з них (
кожного з них (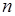 – число сторін многокутника), наближено покладали:
– число сторін многокутника), наближено покладали: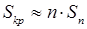 . (8.1)
. (8.1)
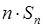 , якщо
, якщо  , де
, де  – радіус круга. Це й є точна формула для площі круга.
– радіус круга. Це й є точна формула для площі круга.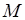 , яка рухається вздовж прямої. Нехай за час
, яка рухається вздовж прямої. Нехай за час  ця точка пройшла відстань
ця точка пройшла відстань 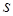 . Відомо, що середня швидкість руху на цій ділянці шляху обчислюється за формулою:
. Відомо, що середня швидкість руху на цій ділянці шляху обчислюється за формулою: .
.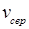 при прямуванні проміжку часу
при прямуванні проміжку часу  , то множину чисел
, то множину чисел  називають числовою послідовністю (або просто послідовністю).
називають числовою послідовністю (або просто послідовністю). утворює послідовність – тут кожному натуральному числу
утворює послідовність – тут кожному натуральному числу  та геометрична
та геометрична  прогресії.
прогресії. , для арифметичної прогресії
, для арифметичної прогресії  , а для геометричної
, а для геометричної  .
. ,
, ,
, ,
, ,
,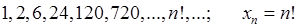 .
. (
( .
.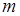 ) перших членів послідовності і вказується правило, за яким за відомими послідовними
) перших членів послідовності і вказується правило, за яким за відомими послідовними 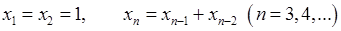
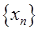 .
.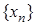 називається обмеженою зверху, якщо існує число
називається обмеженою зверху, якщо існує число  таке, що
таке, що  виконано:
виконано: 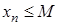 .
. таке, що
таке, що  .
. таке, що
таке, що  виконано:
виконано: 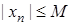 .
. обмежена зверху (але не обмежена знизу), послідовність
обмежена зверху (але не обмежена знизу), послідовність  обмежена знизу (але не обмежена зверху), а послідовність
обмежена знизу (але не обмежена зверху), а послідовність  обмежена.
обмежена. (
(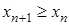 ).
). (
( ).
).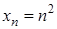 – зростаюча, послідовність
– зростаюча, послідовність 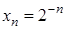 – спадна, послідовність
– спадна, послідовність 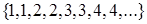 – неспадна, послідовність
– неспадна, послідовність  – незростаюча.
– незростаюча.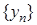 називається послідовність
називається послідовність  (кожен член цієї послідовності дорівнює сумі відповідних членів послідовностей
(кожен член цієї послідовності дорівнює сумі відповідних членів послідовностей  . Відмітимо на числовій прямій точки, які відповідають декілька першим членам цієї послідовності.
. Відмітимо на числовій прямій точки, які відповідають декілька першим членам цієї послідовності.
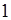

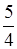

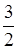
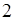
 числової осі, який містить точку 1. Цей інтервал є 0,2–околом точки 1, і
числової осі, який містить точку 1. Цей інтервал є 0,2–околом точки 1, і 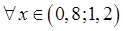 виконана нерівність
виконана нерівність 
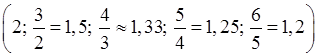 не належать вказаному інтервалу (нагадаємо, що межа 1,2 інтервалу цьому інтервалу не належить). А вся решта елементів, починаючи з шостого
не належать вказаному інтервалу (нагадаємо, що межа 1,2 інтервалу цьому інтервалу не належить). А вся решта елементів, починаючи з шостого  , опиняються всередині його, отже для них буде виконано нерівність:
, опиняються всередині його, отже для них буде виконано нерівність:
 такий, що, починаючи з наступного за ним, тобто
такий, що, починаючи з наступного за ним, тобто  , всі елементи послідовності будуть задовольняти нерівність (8.2).
, всі елементи послідовності будуть задовольняти нерівність (8.2). , тобто 0,1–окіл точки 1. І для цього околу спостерігається ситуація, аналогічна попередній. Цього разу перші 10 елементів нашої послідовності
, тобто 0,1–окіл точки 1. І для цього околу спостерігається ситуація, аналогічна попередній. Цього разу перші 10 елементів нашої послідовності 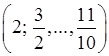 вказаному околу не належать, а решта, починаючи з 11-го
вказаному околу не належать, а решта, починаючи з 11-го 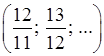 , належать, і для них виконано нерівність
, належать, і для них виконано нерівність .
. , то помітимо, що, починаючи з номера, наступного за
, то помітимо, що, починаючи з номера, наступного за  , всі елементи послідовності
, всі елементи послідовності 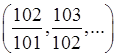 потрапляють всередину цього околу, а за його межами залишається лише скінчена кількість елементів послідовності
потрапляють всередину цього околу, а за його межами залишається лише скінчена кількість елементів послідовності  , тобто буде виконано нерівність
, тобто буде виконано нерівність 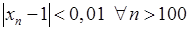 .
. такий, що починаючи з наступного за ним, всі елементи послідовності потраплять всередину цього околу (тобто нескінченна їх кількість), а за його межами буде міститися лише скінчена кількість елементів послідовності. У першому з розглянутих випадків номер
такий, що починаючи з наступного за ним, всі елементи послідовності потраплять всередину цього околу (тобто нескінченна їх кількість), а за його межами буде міститися лише скінчена кількість елементів послідовності. У першому з розглянутих випадків номер  , де
, де 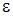 – мале додатне число, тобто розглянемо
– мале додатне число, тобто розглянемо 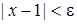 .
. (тут
(тут 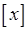 – ціла частина числа
– ціла частина числа  будуть належати інтервалу
будуть належати інтервалу  . Таким чином, номер
. Таким чином, номер 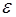 , який визначає довжину інтервалу. Тобто встановили наступне:
, який визначає довжину інтервалу. Тобто встановили наступне: (тобто
(тобто  виконана нерівність:
виконана нерівність: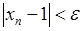 .
.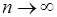 , і пишуть:
, і пишуть: .
. – скорочення від limes – границя).
– скорочення від limes – границя). .
.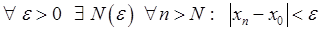 .
. .
.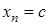 . Покажемо, що
. Покажемо, що  . Задамо довільне
. Задамо довільне  . Очевидно, що нерівність
. Очевидно, що нерівність 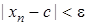 виконується для будь якого
виконується для будь якого  , отже у якості
, отже у якості 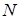 можна взяти 1.
можна взяти 1.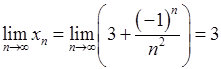 .
.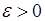 і розглянемо:
і розглянемо: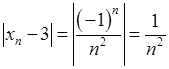 .
.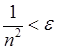 .
. , або
, або  . Отже, якщо
. Отже, якщо 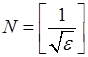 , то для всіх елемен-
, то для всіх елемен- , буде виконано:
, буде виконано:  . Таким чином,
. Таким чином, 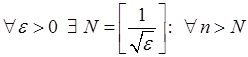 виконано
виконано 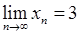 .
. .
.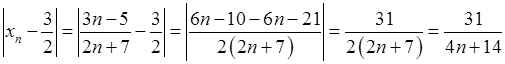 .
. , то
, то  . Таким чином, якщо
. Таким чином, якщо  , то, починаючи з номера
, то, починаючи з номера  . Отже
. Отже 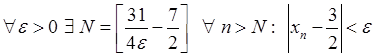 , що й треба було довести.
, що й треба було довести. не має ніякої
не має ніякої . Припустимо, що існує
. Припустимо, що існує  . Тоді, починаючи з номера
. Тоді, починаючи з номера  .
. . Тоді
. Тоді  , оскільки будь які два сусідні члени послідовності відрізняються на 2. З іншого боку:
, оскільки будь які два сусідні члени послідовності відрізняються на 2. З іншого боку: .
. . Це й показує, що у даної послідовності не існує границі.
. Це й показує, що у даної послідовності не існує границі. такий, що
такий, що 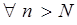 виконано нерівність
виконано нерівність  , то кажуть, що
, то кажуть, що  .
.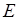 .
. .
.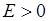 і розглянемо нерівність:
і розглянемо нерівність: .
. , або
, або  .
.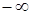 та
та  . Вони визначаються так:
. Вони визначаються так: , то кажуть, що
, то кажуть, що 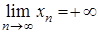 .
. , то кажуть, що
, то кажуть, що  .
. ,
, 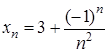 – збіжні, а послідовності
– збіжні, а послідовності  ,
,  ,
,  – розбіжні.
– розбіжні.


