Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интервальные оценки. Доверительная вероятность и доверительный интервал
Рассмотренные точечные оценки параметров распределения дают оценку в виде числа, наиболее близкого к значению неизвестного параметра. Такие оценки используют обычно при большом числе измерений. Чем меньше объем выборки, тем легче допустить ошибку при выборе параметра. Для практики важно не только получить точечную оценку, но и определить интервал, называемый доверительным, между границами которого с заданной доверительной вероятностью
где находится истинное значение оцениваемого параметра. 1.В общем случае, при любом законе распределения СВ, доверительные интервалы можно определять, на основе неравенства Чебышева. Оно определяет вероятность того, что результат измерения не отличается от среднего значения больше чем на половину доверительного интервала
где Принимая доверительную вероятность Р из неравенства можно определить значение t (табл.2.4).
Таблица 2.4 Таблица вероятностей распределения Чебышева
Полученные с помощью неравенства Чебышева интервалы оказываются слишком широкими для практики. Так, доверительной вероятности 0,9 для многих законов распределений соответствует доверительный интервал 1,6s, а по неравенству Чебышева 3,16s. В связи с этим оно не получило широкого распространения. 2. Для нормально распределенной СВ и при большом количестве наблюдений (измерений), интервальная оценка определяется следующим образом: - определяется точечная оценка МО и СКО по приведенным выше формулам; - выбирается доверительная вероятность Р из рекомендуемого ряда значений 0,90; 0,95; 0,99; - находятся верхняя
где n – количество измеренных значений(объем выборки); Полученный доверительный интервал удовлетворяет условию
3. Для нормально распределенной СВ, но при малом количестве наблюдений (измерений), что обычно бывает на практике, верхняя
А половина длины доверительного интервала равна
где 4. В тех случаях, когда распределение СВ не является нормальным, все же часто пользуются распределением Стьюдента с приближением, степень которого остается неизвестной. Распределение Стьюдента применяют при числе измерений n < 30, поскольку уже при n = 20¸30 оно переходит в нормальное. Результат измерения записывается в виде Множитель Полученный результат измерения не является одним конкретным числом, а представляет собой интервал, внутри которого с некоторой вероятностью Пример 2.1. Произведено 50 измерений постоянного сопротивления. Определить доверительный интервал для математического ожидания значения постоянного сопротивления, если закон распределения нормальный с параметрами Решение. При нормальном законе распределения доверительный интервал определяется по формуле (2.44). В соответствии с заданием доверительная вероятность
Окончательно Данный способ нахождения доверительных интервалов справедлив для достаточно большого числа наблюдений Доверительный интервал при заданной вероятности тем менее надежен, чем меньше число наблюдений.
Пример 2.2. Определение удельных магнитных потерь для различных образцов одной партии электротехнической стали марки 2212 дало следующие результаты: 1,21; 1,17; 1,18;1,13;1,19;1,14;1,20 и 1,18 Вт/кг. Считая, что систематическая погрешность отсутствует, а случайная распределена по нормальному закону, требуется определить доверительный интервал при значениях доверительной вероятности 0,9 и 0,95. Для решения задачи использовать формулу Лапласа и распределение Стьюдента.
Решение. По формулам (2.34) и (2.37) находим оценки среднего арифметического значения и СКО результатов измерений. Они соответственно равны 1,18 и 0,0278 Вт/кг. Считая, что оценка СКО равна самому отклонению, находим:
Отсюда, используя значения функции Лапласа, приведенные в таблице П 1, определяем, что В том случае, когда нет оснований считать, что СКО и его оценка равны, доверительный интервал определяется на основе распределения Стьюдента:
По табл. П 2 находим, что t0,9 = 1,9 и t0,95 = 2,37. Отсюда доверительные интервалы соответственно равны 1,18 ± 0,019 и 1,18 ± 0,023 Вт/кг.
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 785; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.38.3 (0.011 с.) |
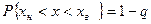 , (2.41)
, (2.41)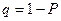 - уровень значимости;
- уровень значимости; 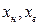 - нижняя и верхняя границы интервала,
- нижняя и верхняя границы интервала,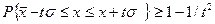 , (2.42)
, (2.42)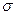 оценка СКО распределения;
оценка СКО распределения; 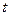 - положительное число.
- положительное число.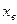 и нижняя
и нижняя 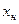 границы доверительного интервала по уравнениям
границы доверительного интервала по уравнениям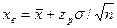 ,
, 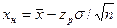 , (2.43)
, (2.43)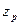 - аргумент функции Лапласа
- аргумент функции Лапласа 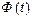 , отвечающей вероятности Р/2. Половина длины доверительного интервала
, отвечающей вероятности Р/2. Половина длины доверительного интервала 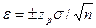 , называется доверительной границей погрешности результата измерений.
, называется доверительной границей погрешности результата измерений.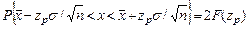 . (2.44)
. (2.44)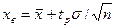 ,
, 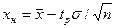 (2.45)
(2.45)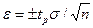 ,
,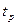 -коэффициент Стьюдента, рассчитанный для различных значений доверительной вероятности и числа измерений, табулирован.
-коэффициент Стьюдента, рассчитанный для различных значений доверительной вероятности и числа измерений, табулирован.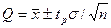 ;
; 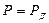 , где
, где 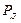 – конкретное значение доверительной вероятности.
– конкретное значение доверительной вероятности.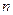 равен квантильному множителю
равен квантильному множителю 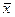 не означает, что истинное значение ближе к нему, чем к остальным точкам интервала. Оно может быть в любом месте интервала, а с вероятностью
не означает, что истинное значение ближе к нему, чем к остальным точкам интервала. Оно может быть в любом месте интервала, а с вероятностью 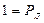 даже вне его.
даже вне его.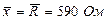 ,
, 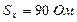 при доверительной вероятности
при доверительной вероятности 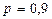 .
.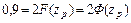 . Отсюда
. Отсюда 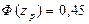 . Из таблицы П1 находим, что
. Из таблицы П1 находим, что 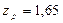 . Следовательно, доверительный интервал запишется в виде
. Следовательно, доверительный интервал запишется в виде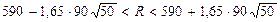 .
.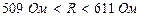 .
.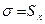 . Вычисляемая оценка
. Вычисляемая оценка 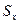 является лишь приближением к истинному значению
является лишь приближением к истинному значению 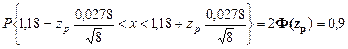
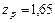 . Для
. Для 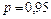 коэффициент
коэффициент 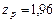 .Доверительные интервалы, соответствующие р = 0,9 и 0,95 равны 1,18 ± 0,016 и 1,18 ± 0,019 Вт/кг.
.Доверительные интервалы, соответствующие р = 0,9 и 0,95 равны 1,18 ± 0,016 и 1,18 ± 0,019 Вт/кг.