
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Параметричний тест Голдфелда-КвондтаСтр 1 из 5Следующая ⇒
Параметричний тест Голдфелда-Квондта Цей тест застосовується в основному для невеликих вибірок. В основу цього тесту покладено припущення, що дисперсія залишків зростає пропорційно до квадрату однієї з пояснюючих змінних xj, тобто розглядається випадок коли Алгоритм тесту Крок 1. Виконується впорядкування (ранжування) спостережень у статистичній вибірці в порядку зростання (або спаду) значень пояснюючої змінної xj. Крок 2. З усіх спостережень впорядкованої вибірки відкидається с спостережень, які містяться у центрі вибірки. Ця кількість згідно рекомендацій авторів тесту визначається із співвідношення
У результаті цього утворюються дві підвибірки розміром Крок 3. Для кожної підвибірки на основі 1МНК будується окрема регресійна модель. Крок 4. Для кожної підвибірки визначається сума квадратів залишків SSE1 і SSE2:
де е1,i – залишки для першої моделі (побудованої на основі першої підвибірки), е2,i –залишки для другої моделі(побудованої на основі другої підвибірки). Крок 5. Для порівняння зазначених дисперсій обчислюється наступна F – статистика (критерій Фішера):
яка порівнюється з табличним значення F – критерію Fтабл Якщо виконується умова F* > Fтабл, то гетероскедастичність присутня. У протилежному випадку маємо випадок гомоскедастичності. 2) Узагальнений метод найменших квадратів Нехай задано економетричну модель
коли Задача полягає в знаходженні оцінок елементів вектора А в моделі. Для цього використовується матриця S, за допомогою якої коригується вихідна інформація. Базуючись на особливостях матриць Р і S, які були розглянуті в підрозд. 7.3, можна записати співвідношення між цими матрицями та оберненими до них. Оскільки S — додатно визначена матриця, то вона може бути зображена як добуток
Помноживши рівняння (7.1) ліворуч на матрицю
Позначимо
Тоді модель матиме вигляд:
Використовуючи (7.3), неважко показати, що
тобто модель (7.6) задовольняє умови (4.2), коли параметри моделі можна оцінити на основі 1МНК. Звідси
Ця оцінка є незміщеною лінійною оцінкою вектора А, який має найменшу дисперсію і матрицю коваріацій
Hезміщену оцінку для дисперсії
Оцінка параметрів При заданій матриці S оцінку параметрів моделі можна обчислити згідно із (7.7), а стандартну помилку — згідно із (7.8). Тому можна сконструювати звичайні критерії значущості і довірчі інтервали для параметрів Визначивши залишки
або Звідси Тоді Оскільки то Кореляційний аналіз При проведенні кореляційного аналізу сукупність даних розглядається як безліч змінних (чинників), кожна з яких містить n спостережень; xik – спостереження i змінної k; – середнє значення k-ї змінної; i=1,...,n. Парні коефіцієнти кореляції Парний коефіцієнт кореляції між k-м і L-м чинниками обчислюється за формулою:
Він є показником тісноти лінійного статистичного зв'язку, але тільки у разі спільного нормального розподілу випадкових величин, вибірками яких є k-й і L-й чинники. За таких умов для перевірки гіпотези про рівність нулю парного коефіцієнта кореляції використовується t-статистика, розподілена згідно із законом Стьюдента з n-2 ступенями свободи. Часткові коефіцієнти кореляції Частковий коефіцієнт кореляції першого порядку між k-м і L-м чинниками характеризує тісноту їх лінійного зв'язку при фіксованому значенні j-го чинника. Він визначається як
Він розподілений аналогічно парному коефіцієнту за таких самих передумов, і для перевірки його значеннєвості використовується t-статистика, в якій число ступенів свободи дорівнює n-3. У програмі частковий коефіцієнт кореляції розраховується в загальному вигляді, тобто за умови, що решта всіх змінних - фіксовані:
Тут Dij — визначник матриці, утвореної з матриці парних коефіцієнтів кореляції викреслюванням i-го рядка і j-го стовпчика.
Множинні коефіцієнти кореляції Для визначення тісноти зв’язку між поточною k-ю змінною і змінними, що залишились, використовується вибірковий множинний коефіцієнт кореляції:
де D - визначник матриці парних коефіцієнтів кореляції. Для перевірки статистичної значущості коефіцієнта множинної кореляції використовується величина:
Якщо розраховане F-значення більше значення F-розподілу на відповідному рівні імовірності (0.9 і вище), то гіпотеза про лінійний зв'язок між k-ю змінною і рештою змінних не заперечується. НАСЛІДКИ АВТОКОРЕЛЯЦІЇ Оцінки параметрів моделі можуть бути незміщеними, але неефективними, тобто вибіркові дисперсії вектора оцінок а можуть бути невиправдано великими.
Області визначення DW Критерій Дарбіна — Уотсона Крок 1. Розраховується значення d-статистики за формулою
Зауваження. Доведено, що значення d-статистики Дарбіна - Уотсона перебуває в межах 0 < DW< 4. Крок 2. Задаємо рівень значущості а. За таблицею Дарбіна - Уотсона при заданому рівні значущості а, кількості факторів m і кількості спостережень n знаходимо два значення DW1 і DW2: . Якщо 0< DW< DW1, то наявна додатна автокореляція. . ЯкщоDW 1 <DW< DW2 або 4 - DW2< DW< 4 - D W, ми не можемо зробити висновки ані про наявність, ані про відсутність автокореляції (DW потрапляє в зону невизначеності). . Якщо 4-DW1 < DW < 4, маємо від’ємну автокореляцію. . Якщо DW < DW < 4-DW2, то автокореляція відсутня. Критерій Дарбіна - Уотсона. Для перевірки наявності автокореляції відхилень обчислюють статистику d за формулою:
де lt - величина відхилень в період t, n - кількість спостережень. Ця статистика може приймати будь-яке значення з інтервату (0,4). Між статистикою d і коефіцієнтом автокореляції існує приблизна залежність
При відсутності автокореляції r = 0 і d статистика приймає значення близькє до 2. При достатньо великій кількості спостережень, можна вважати, що використовується рівність D = 2(1 - r) Якщо r Є (0,1), то d є (0,2) і автокореляція додатня. Для статистики d табульовані критичні межі: нижня d1, та верхня d2. Критичні межі статистики d дозволяють з надійністю Р = 0.95 або P = 0.99, робити висновок про наявність або відсутність автокореляції першого порядку. Якщо 0 < d < dі,то відхилення мають автокореляцію; Якщо d>d2 то приймається гіпотеза про відсутність автокореляції відхилень Якщо d1<d<d2,то висновку робити не можна, а необхідно подальші дослідження, беручи більшу кількість спостережень. При наявності автокореляції відхилень необхідно з'ясувати причини її появи. Для оцінювання параметрів економетричної моделі, з автокорельованими відхиленнями існує декілька методів: загальний метод найменших квадратів для випадку автокореляції і Ейткена), метод перетворення вихідної інформації та наближені методи Дарбіна і Кочрена – Орката.
Метод перетворення вихідної інформації здійснюється у випадку автокореляції відхилень першого порядку за таким алгоритмом: Крок 1. Велечину р, яка характеризує коваріацію відхилень (зв'язок між послідовними елементами ряду відхилень), знаходять за формулою:
де l – величина відхилення у період t, n – кількість спостережень, m – кількість факторів. Крок 2. Будують матрицю перетворень розміром n*n вигляду:
Ця матриця дозволяє застосувати метод найменших квадратів до перетворення вихідних даних:
де xjk – значення катої компоненти фактора Хj. Крок 3. Знаходять оцінки параметрів моделі за формулою
Тест Глейсера Ще один тест для перевіркигетероскедастичностісклавГлейсер. Вінзапропонуваврозглядатирегресіюабсолютнихзначеньзалишків 1) 2) 3) 30.Тест Глейсера. 1) 2) 3) Рішення про відсутність гетероскедастичності залишків приймається на підставі статистичної значущості коефіцієнтів Визначення матриці Щоб оцінити параметри моделі, коли дисперсії залишків визначаються Оскільки явище гетероскедастичності пов'язане лише з тим, що змінюються дисперсії залишків, а коваріація між ними немає, то матриця Звідси в матриці b) c) Для першої гіпотези: Для другої гіпотези:
Для третьої гіпотези Оскільки матриця Параметричний тест Голдфелда-Квондта Цей тест застосовується в основному для невеликих вибірок. В основу цього тесту покладено припущення, що дисперсія залишків зростає пропорційно до квадрату однієї з пояснюючих змінних xj, тобто розглядається випадок коли Алгоритм тесту Крок 1. Виконується впорядкування (ранжування) спостережень у статистичній вибірці в порядку зростання (або спаду) значень пояснюючої змінної xj. Крок 2. З усіх спостережень впорядкованої вибірки відкидається с спостережень, які містяться у центрі вибірки. Ця кількість згідно рекомендацій авторів тесту визначається із співвідношення
У результаті цього утворюються дві підвибірки розміром Крок 3. Для кожної підвибірки на основі 1МНК будується окрема регресійна модель. Крок 4. Для кожної підвибірки визначається сума квадратів залишків SSE1 і SSE2:
де е1,i – залишки для першої моделі (побудованої на основі першої підвибірки), е2,i –залишки для другої моделі(побудованої на основі другої підвибірки). Крок 5. Для порівняння зазначених дисперсій обчислюється наступна F – статистика (критерій Фішера):
яка порівнюється з табличним значення F – критерію Fтабл Якщо виконується умова F* > Fтабл, то гетероскедастичність присутня. У протилежному випадку маємо випадок гомоскедастичності. 2) Узагальнений метод найменших квадратів Нехай задано економетричну модель
коли Задача полягає в знаходженні оцінок елементів вектора А в моделі. Для цього використовується матриця S, за допомогою якої коригується вихідна інформація. Базуючись на особливостях матриць Р і S, які були розглянуті в підрозд. 7.3, можна записати співвідношення між цими матрицями та оберненими до них. Оскільки S — додатно визначена матриця, то вона може бути зображена як добуток
Помноживши рівняння (7.1) ліворуч на матрицю
Позначимо
Тоді модель матиме вигляд:
Використовуючи (7.3), неважко показати, що
тобто модель (7.6) задовольняє умови (4.2), коли параметри моделі можна оцінити на основі 1МНК. Звідси
Ця оцінка є незміщеною лінійною оцінкою вектора А, який має найменшу дисперсію і матрицю коваріацій
Hезміщену оцінку для дисперсії
Оцінка параметрів При заданій матриці S оцінку параметрів моделі можна обчислити згідно із (7.7), а стандартну помилку — згідно із (7.8). Тому можна сконструювати звичайні критерії значущості і довірчі інтервали для параметрів
Визначивши залишки
або Звідси Тоді Оскільки то
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 243; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.239.148 (0.098 с.) |
 , де
, де  - невідомий коефіцієнт пропорційності (константа). Залишки, при цьому розподілені за нормальним законом і некорельовані.
- невідомий коефіцієнт пропорційності (константа). Залишки, при цьому розподілені за нормальним законом і некорельовані. . (6)
. (6) .
. , (7)
, (7)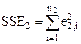 , (8)
, (8)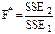 , (9)
, (9) (7.1)
(7.1)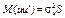 .
.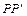 , де матриця P є невиродженою, тобто:
, де матриця P є невиродженою, тобто: , (7.2) коли
, (7.2) коли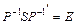 ; (7.3) і
; (7.3) і . (7.4)
. (7.4) , дістанемо:
, дістанемо: . (7.5)
. (7.5) ;
; ;
; .
.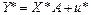 . (7.6)
. (7.6) ,
, . (7.7)
. (7.7) (7.8)
(7.8) можна дістати так:
можна дістати так: (7.9)
(7.9) , яку знайдено за допомогою (7.7), є оцінкою узагальненого методу найменших квадратів (методу Ейткена).
, яку знайдено за допомогою (7.7), є оцінкою узагальненого методу найменших квадратів (методу Ейткена). .
.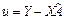 і помноживши ліворуч на матрицю
і помноживши ліворуч на матрицю  ,
, .
. .
. .
. (7.10)
(7.10)





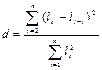 (7.1)
(7.1)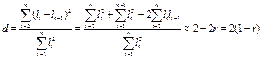 (7.2)
(7.2) (7.3)
(7.3)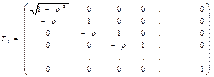 (7.4)
(7.4)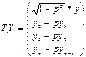
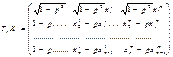
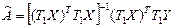 (7.5)
(7.5)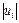 ,щовідповідаютьрегресіїнайменшихквадратів, як певнуфункціювід
,щовідповідаютьрегресіїнайменшихквадратів, як певнуфункціювід 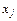 , де
, де 

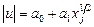 і т.ін.
і т.ін. , які відповідають регресії найменших квадратів, як певну функцію
, які відповідають регресії найменших квадратів, як певну функцію  , де
, де  . Для цього використовуються такі види функцій:
. Для цього використовуються такі види функцій: ;
; ;
; и т. д.
и т. д. і
і  . Переваги цього тесту визначаються можливістю розрізняти випадки чистою і змішаної гетероскедастичності. Чистої гетероскедастичності відповідають значення параметрів
. Переваги цього тесту визначаються можливістю розрізняти випадки чистою і змішаної гетероскедастичності. Чистої гетероскедастичності відповідають значення параметрів  и
и  , а змішаної –
, а змішаної –  і
і  . Залежно від цього, потрібно користуватися різними матрицями
. Залежно від цього, потрібно користуватися різними матрицями  . Нагадаємо, що
. Нагадаємо, що 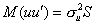 .
.
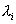 можна обчислити, користуючись гіпотезами:
можна обчислити, користуючись гіпотезами: , тобто дисперсія залишків пропорційна до зміни пояснювальній змінної
, тобто дисперсія залишків пропорційна до зміни пояснювальній змінної  ;
; , тобто зміна дисперсії пропорційно до зміни квадрата пояснювальній змінної
, тобто зміна дисперсії пропорційно до зміни квадрата пояснювальній змінної  ;
; , тобто дисперсія залишків пропорційна до зміни квадрата залишків по модулю.
, тобто дисперсія залишків пропорційна до зміни квадрата залишків по модулю. .
. .
. , або
, або 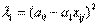 , або
, або  .
.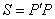 матрица
матрица  має вигляд:
має вигляд:


