
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Представлення числової інформації в цифровому автоматі
Система числення - це сукупність прийомів і правил для записи чисел з цифровими знаками. Запис числа у деякій системі числення часто називають кодом числа. Елементи (символи) алфавіту, які використовуються для запису чисел в деякій системі числення, прийнято називати цифрами. Кожній цифрі даного числа однозначно зіставляється її кількісний (Числовий) еквівалент. Розрізняють позиційні і непозиційної системи числення. Непозиційною система числення - це система, для якої значення символу, тобто цифри, НЕ залежить від його положення в числі. До таких систем відноситься, зокрема, римська система (правда з деякими застереженнями). Тут, наприклад, символ V завжди означає п'ять, незалежно від місця його появи в записі числа. Є й інші сучасні непозиційної системи. Позиційна система числення - це система, в якої значення кожній цифри залежить від її числового еквівалента і від її місця (позиції) в числі, тобто один і той-же символ (цифра) може приймати різні значення. Будь-яка позиційна система числення характеризується підставою або базисом. Базис q природної позиційної системи числення – це кількість знаків (символів), що використовуються для зображення чисел в даній системі. Тому стає можлива теорія, про незліченну безліч позиційних систем за основу яких можна прийняти будь-яке число, просто утворивши нову систему числення. Коли ми уявляємо або записуємо деяке число, в позиційній системі числення - ми розміщуємо відповідні цифри цього числа, по окремим позиціям. Ці позиції прийнято називати розрядами числа в даній позиційній системі числення, кількість розрядів у записі числа називається розрядністю числа і збігається з його довжиною. Арифметичні дії з двійковими числами Алгебраїчне додавання Додавання здійснюється послідовно, починаючи з молодшого розряду. У кожному розряді додаються значення трьох величин: розряду операнда аі, розряду операнда bі, та переносу з попереднього розряду pi-1. У результаті додавання в кожному розряді одержуємо дві величини: значення суми sі, та значення переносу в наступний, більш старший розряд.
Операція машинного множення Множення двійкових чисел виконують у прямому коді. Знак добутку визначають за знаковими розрядами множеного і множника у відповідності з таким правилом: якщо знак операндів однаковий, то знак добутку - позитивний; у противному випадку знак добутку негативний. Знак добутку двох чисел не впливає на алгоритм виконання операції множення модулів цих чисел. Найпростішим способом множення є багаторазове додавання, що полягає в додаванні множеного самого із собою, причому число таких операцій дорівнює множнику. Такий алгоритм множення є простим, але повільним. Часто використовують спосіб множення, процедура якого аналогічна процедурам множення вручну. У цьому випадку результат одержують додаванням часткових добутків, що є результатом множення множеного на значення чергових розрядів множника. Кожен частковий добуток удвічі перевищує попереднє значення, що відповідає зрушенню його ліворуч на один розряд. Операції машинного ділення В універсальних обчислювальних машинах, як правило, реалізується "шкільний" алгоритм ділення чисел. "Шкільний" алгоритм ділення полягає в тому, що дільник на кожному кроці віднімається від діленого стільки разів (починаючи зі старших розрядів), скільки це можливо для отримання найменшого позитивного залишку. Тоді в черговий розряд частки записується цифра, що дорівнює числу дільників, що містяться в діленому на даному кроці. При діленні операцію віднімання повторюють до тих пір, поки ділене не стане менше дільника. Існують і інші алгоритми, наприклад, алгоритм ділення з відновленням залишку, та алгоритм ділення без відновлення залишку. Контроль за модулем Контроль за модулем визнаний одним з основних методів функціонального діагностування обчислювальних пристроїв (ОП). Однак реалізація контролю за модулем для сучасних ВУ є складним завданням, що пов'язано з високими вимогами, які пред'являються до продуктивності ВУ, діапазону представлення чисел і точності обчислень. Такому рівню вимог відповідають матриці обчислювального пристрою з плаваючою точкою, в яких мантиси чисел обробляються зі збереженням єдиних форматів представлення операндів і результатів. Витрати обладнання і часу обчислень в матричних обчислювальних пристроях знаходяться відповідно в квадратичної і лінійної залежності від розрядності оброблюваних чисел. Для зниження цих витрат доцільно використовувати методи скороченого виконання операцій. Однак скорочення обчислень суперечить використанню традиційного контролю за модулем, вимагаючи його розвитку. Завдання контролю за модулем скороченою операції вирішена для матричного помножувача, що забезпечує для ВУ одночасно і високу достовірність функціонування і високі схемо-технічні показники, близькі до двократного зниження витрат обладнання і підвищення швидкодії. Розподіл чисел є найскладнішою арифметичною операцією і вимагає для її реалізації найбільших витрат обладнання і часу. Пропонується скорочене виконання операції ділення - її контроль за модулем.
Найбільш часто в матричних ВУ використовуються алгоритми ділення з відновленням і без відновлення залишку. Існує два методи отримання контрольного коду: числовий і цифровий. Мінімізація функцій перемикання Метод Квайна Цей метод базується на перетвореннях досконалої диз’юнктивної нормальної форми за допомогою операції неповного склеювання та поглинання. Операція (повного) склеювання визначається співвідношенням: Справедливість даного виразу випливає з такого перетворення: Операція поглинання визначається співвідношенням: Кажуть, що член xy поглинається є членом x. Справедливість сказаного випливає з перетворень: Операція неповного склеювання, що застосована в методі Квайна, визначається формулою Теорема Квайна Якщо в досконалій диз’юнктивній нормальній формі логічної функції провести всі операції неповного склеювання, а потім всі операції поглинання, то вийде скорочена диз’юнктивна нормальна форма цієї функції, тобто диз’юнкція всіх її простих імплікант. З теореми Квайна випливає – якщо функція задана у довільній формі, то її слід перетворити в досконалу ДНФ, застосувати функцію розгортання, і лише після цього проводити операції склеювання і поглинання. Метод Петрика Метод використовується для знаходження всіх мінімальних покриттів конституант одиниці і дозволяє отримати всі тупикові ДНФ по імплікантній матриці. Суть методу полягає в наступному. За імплікантною матрицею будується, так зване кон'юнктивне уявлення імплікантной матриці. Для цього всі прості імпліканти позначаються різними літерами (зазвичай великими латинськими). Після цього, для кожного стовпчика імплікантної матриці будується диз'юнкція всіх букв, що позначають рядки матриці, перетин яких з стовпцем відзначено хрестиком. Кон'юнктивні уявлення імплікантної матриці утворюється як кон'юнкція побудованих диз'юнкцій для всіх стовпців матриці. До кон'юнктивного подання матриці можуть бути застосовані всі співвідношення булевої алгебри, з метою його спрощення. Після розкриття дужок і виконання всіх можливих поглинань виходить диз'юнкція і кон'юнкція, кожна з яких містить всі імпліканти тупикової ДНФ.
Метод Квайна-Мак-Класкі Метод Квайна-Мак-Класкі (метод простих імплікант) – табличний метод мінімізації булевих функцій, розроблений Вілардом Квайном і Едвардом Мак-Класкі. Функціонально він ідентичний картам Карно, але таблична форма робить його ефективнішим для використання в комп'ютерних алгоритмах. Алгоритм мінімізації Терми (кон'юнктивні - в разі СДНФ і диз'юнктивні - в разі СКНФ), на яких визначена ФАЛ записуються у вигляді їх довічних еквівалентів. Ці еквіваленти розбиваються на групи, в кожну групу входять еквіваленти з рівною кількістю одиниць (нулів). Проводиться попарне порівняння еквівалентів (термів) в сусідніх групах, з метою формування термів нижчих рангів. Складається таблиця з заголовком рядків, в якій є вихідні терми, а в заголовках стовпців є терми низьких рангів. Розставляються мітки, що відображають поглинання термів вищих рангів (вихідних термів) і далі мінімізація проводиться за методом Квайна.
|
|||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 271; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.2.15 (0.008 с.) |
 .
. .
. .
. /
/ , яка може бути отримана з формул: x=x
, яка може бути отримана з формул: x=x  =x
=x 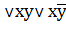 .
.


