Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Фундаментальная система решений линейного однородного уравнения ⇐ ПредыдущаяСтр 5 из 5
Определение. Любые Из предыдущих теорем сразу следует еще одна важная теорема. Теорема 7. Решения Доказательство. Равносильная переформулировка утверждения теоремы – решения Теорема 8. Для любого линейного однородного дифференциального уравнения (2) существует фундаментальная система его решений. Доказательство. Построим такую фундаментальную систему решений. Для этого возьмем произвольную точку По теореме 1 о существовании и единственности у каждой из этих задач имеется решение, и мы обозначим Теорема 9. Пусть Доказательство. Возьмем произвольную точку Замечание. Теоремы 8 и 9 означают, что размерность векторного пространства решений уравнения (2) равна значениями
Замечание. Теоремы 8 и 9 означают, что размерность векторного пространства решений уравнения (2) равна
Билет №15 Структура общего решения неоднородной системы Любые n – r линейно независимых решений системы называются ее фундаментальной системой решений.
Билет №16 Линейный оператор в Линейные операторы. Матрица линейного оператора. Примеры линейных операторов. Определение. Если каждому элементу Результат действия оператора A на элемент Если элементы Множество элементов пространства Rn, для которых определено действие оператора A, называют областью определения оператора A и обозначают D ( A). Множество элементов пространства Rn, которые являются образами элементов из области определения D ( A) оператора A, называют образом оператора A и обозначают Im(A). Если Ядром оператора называется множество элементов пространства Rn, образом которых является нуле нулевой элемент. Ядро оператора обозначают Ker(A):
Определение. Оператор A, действующий в пространстве Rn называется линейным оператором, если для любых
Определение. Матрица, столбцами которой являются координаты образов соответствующих базисных векторов некоторого базиса в Rn —
называется матрицей линейного оператора Билет №17 Действия с линейными операторами и их матрицами
Рассмотрим линейный оператор Ядром линейного оператора называется множество элементов из
Для линейного оператора, действующего в n-мерном линейном пространстве сумма ранга и дефекта оператора равно размерности пространства, в котором действует оператор: ранг оператора равен рангу его матрицы; ядро оператора совпадает с множеством решений линейной однородной системы с матрицей столбцы, входящие в базисный минор матрицы оператора образуют базис в образе оператора. Сформулированные утверждения позволяют описать структуру образа и ядра линейного оператора, заданного матрицей, используя язык матричных преобразований и общей теории линейных систем.
Билет №18 Преобразование координат вектора и матрицы линейного оператора. Их свойства и вычисления. Пусть в
Составим матрицу, столбцами которой служат координатные столбцы векторов нового базиса
Эта матрица называется матрицей перехода от старого базиса к новому. Изменение матрицы линейного преобразования при изменении базиса В предыдущем разделе мы установили, что как только в линейном пространстве выбран базис, то каждому линейному преобразованию соответствует матрица этого преобразования. Однако если выбрать в пространстве другой базис, то матрица преобразования, как правило, станет другой. Выясним, как эти матрицы связаны между собой. Пусть Предложение 19.1 Пусть
Доказательство. Пусть Определение 19.2 Две квадратных матрицы Следствие 19.1 Матрицы одного линейного преобразования, соответствующие разным базисам, подобны друг другу, и наоборот, если матрицы подобны, то они являются матрицами одного и того же преобразования в разных базисах.
Билет №19. Собственные значения и собственные векторы линейного оператора. Их свойства и вычисление.
Определение. Пусть A — линейный оператор, действующий в линейном пространстве Rn. Число По теореме о связи координат образа и прообраза имеем: Это означает, что собственный вектор оператора является ненулевым решением линейной однородной системы Легко видеть, что определитель Определение. Уравнение Примеры. 1. Нулевой оператор Свойства собственных векторов Для собственных значений и собственных векторов линейного оператора справедливы следующие утверждения: 1) характеристический многочлен оператора, действующего в Rn является многочленом n -й степени относительно 2) линейный оператор, действующий в Rn, имеет не более n различных собственных значений; 3) собственные векторы оператора определяются с точностью до постоянного сомножителя; поэтому принять вычислять собственные векторы единичной длины — орты собственных векторов; докажем, что если 4) корни характеристического многочлена не зависят от базиса; 5) собственные векторы, отвечающие различным собственным значениям, линейно независимы.
Поверхности 2-го порядка
|
|||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 575; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.40.207 (0.046 с.) |
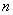 линейно независимых решений линейного однородного дифференциального уравнения
линейно независимых решений линейного однородного дифференциального уравнения 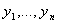 уравнения (2) образуют фундаментальную систему решений этого уравнения тогда и только тогда, когда их определитель Вронского
уравнения (2) образуют фундаментальную систему решений этого уравнения тогда и только тогда, когда их определитель Вронского 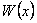 отличен от 0 хотя бы в одной точке
отличен от 0 хотя бы в одной точке 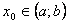 .
.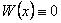 на
на 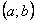 . Но это утверждение сразу следует из теорем 5 и 6.
. Но это утверждение сразу следует из теорем 5 и 6.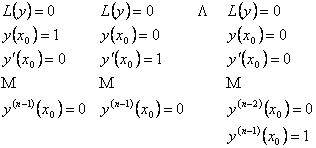 .
.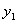 - решение 1-й задачи,
- решение 1-й задачи, 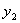 - решение 2-й задачи, …,
- решение 2-й задачи, …, 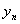 - решение
- решение 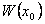 для этих функций:
для этих функций: 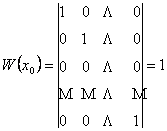 . Следовательно, по теореме 7, функции
. Следовательно, по теореме 7, функции 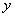 этого уравнения существуют постоянные
этого уравнения существуют постоянные 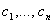 такие, что
такие, что 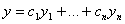 .
.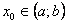 и рассмотрим систему уравнений относительно неизвестных
и рассмотрим систему уравнений относительно неизвестных  (11). Определитель этой системы
(11). Определитель этой системы 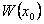 не равен 0, т.к.
не равен 0, т.к. 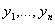 - фундаментальная система решений. Поэтому у нее существует (и притом единственное) решение
- фундаментальная система решений. Поэтому у нее существует (и притом единственное) решение 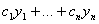 . По теореме 2 она является решением уравнения (2). Ввиду равенств (11) значения этой функции и ее производных до порядка
. По теореме 2 она является решением уравнения (2). Ввиду равенств (11) значения этой функции и ее производных до порядка 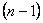 включительно в точке
включительно в точке 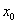 совпадают со значениями
совпадают со значениями 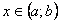 .
.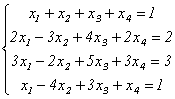
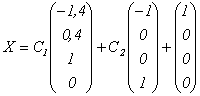
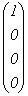 частное решение
частное решение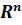 (В линейном пространстве). Матрица линейного пространства
(В линейном пространстве). Матрица линейного пространства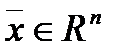 ставится в соответствие единственный элемент
ставится в соответствие единственный элемент  , то говорят, что в пространстве Rn задан оператор, действующий в пространстве Rn.
, то говорят, что в пространстве Rn задан оператор, действующий в пространстве Rn. обозначают
обозначают  .
.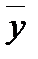 связаны соотношением
связаны соотношением  , то
, то  , то
, то 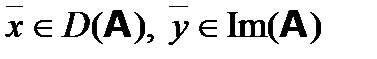 .
.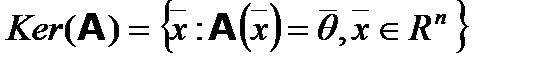 .
.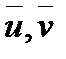 из Rn и для любого числа α справедливо:
из Rn и для любого числа α справедливо: и
и  .
.
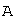 , действующий в конечномерном линейном пространстве
, действующий в конечномерном линейном пространстве 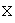 . Доказано, что образ
. Доказано, что образ  линейного оператора
линейного оператора 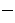 линейное пространство. Размерность образа линейного оператора называется рангом оператора, обозначается
линейное пространство. Размерность образа линейного оператора называется рангом оператора, обозначается  .
. :
: 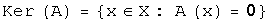 . Ядро линейного оператора
. Ядро линейного оператора 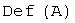 :
: 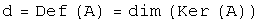 .
.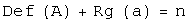 ;
;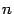 -мерном линейном пространстве
-мерном линейном пространстве  выбран базис
выбран базис 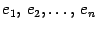 , который мы будем для удобства называть "старый" и другой базис
, который мы будем для удобства называть "старый" и другой базис  , который мы будем называть "новый". Возьмем призвольный вектор
, который мы будем называть "новый". Возьмем призвольный вектор 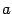 из
из 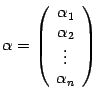 , а в новом --
, а в новом --  . Нам нужно выяснить, как связаны друг с другом координаты в старом и в новом базисе. Для этого нам сначала нужно "связать" друг с другом старый и новый базисы. Запишем разложения новых базисных векторов по старому базису
. Нам нужно выяснить, как связаны друг с другом координаты в старом и в новом базисе. Для этого нам сначала нужно "связать" друг с другом старый и новый базисы. Запишем разложения новых базисных векторов по старому базису

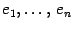 и
и 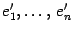 -- два базиса в этом пространстве. Первый из них назовем "старым", а второй -- "новым". Пусть
-- два базиса в этом пространстве. Первый из них назовем "старым", а второй -- "новым". Пусть 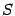 -- матрица перехода 19.1.4 а от старого базиса к новому.
-- матрица перехода 19.1.4 а от старого базиса к новому.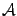 -- линейное преобразование пространства
-- линейное преобразование пространства 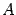 и
и  -- матрицы этого преобразования в старом и новом базисе соответственно. Тогда
-- матрицы этого преобразования в старом и новом базисе соответственно. Тогда
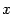 -- произвольный вектор пространства
-- произвольный вектор пространства  -- его образ, то есть
-- его образ, то есть 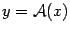 . Пусть
. Пусть 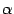 и
и 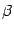 -- координатные столбцы векторов
-- координатные столбцы векторов 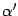 ,
, 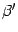 -- в новом. Тогда в силу формулы (19.3)
-- в новом. Тогда в силу формулы (19.3) 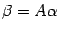 . По предложению 18.5 имеем
. По предложению 18.5 имеем 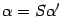 ,
,  . Подставим эти выражения в предыдущую формулу, получаем
. Подставим эти выражения в предыдущую формулу, получаем  . Откуда
. Откуда 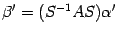 . С другой стороны, в силу формулы (19.3) в новом базисе
. С другой стороны, в силу формулы (19.3) в новом базисе 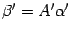 . Сравнивая это равенство с предыдущим, получаем
. Сравнивая это равенство с предыдущим, получаем 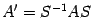 .
. и
и 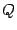 одного порядка называются подобными, если существует такая невырожденная матрица
одного порядка называются подобными, если существует такая невырожденная матрица 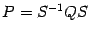 .
. называется собственным значением, а ненулевой вектор
называется собственным значением, а ненулевой вектор  из Rn — соответствующим собственным вектором линейного оператора A, если они связаны между собой соотношением.
из Rn — соответствующим собственным вектором линейного оператора A, если они связаны между собой соотношением.  .
.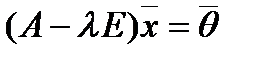 , где E — единичная матрица, а
, где E — единичная матрица, а 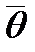 — нулевой вектор Rn.
— нулевой вектор Rn.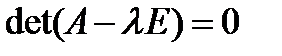 . Следовательно, собственные значения линейного оператора могут быть вычислены как корни уравнения
. Следовательно, собственные значения линейного оператора могут быть вычислены как корни уравнения  , а собственные векторы — как решения соответствующих однородных систем.
, а собственные векторы — как решения соответствующих однородных систем.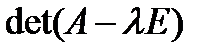 — многочлен n- й степени относительно
— многочлен n- й степени относительно  :
: 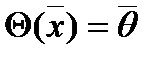 , матрица нулевого оператора — нулевая матрица соответствующего порядка, т.е.
, матрица нулевого оператора — нулевая матрица соответствующего порядка, т.е. 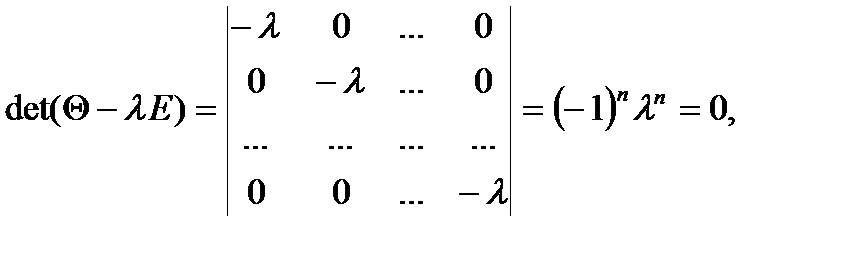 т.е.
т.е. 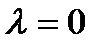 — единственное собственное значение нулевого оператора, а соответствующие собственные векторы — все ненулевые векторы пространства Rn.
— единственное собственное значение нулевого оператора, а соответствующие собственные векторы — все ненулевые векторы пространства Rn. — собственный вектор линейного оператора A, отвечающий собственному значению
— собственный вектор линейного оператора A, отвечающий собственному значению 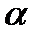 вектор
вектор 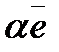 (
( )— собственный вектор оператора A, отвечающий собственному значению
)— собственный вектор оператора A, отвечающий собственному значению  ;
;