Матрица – таблица чисел, состоящая из m строк и n столбцов 
Под линейными операциями над матрицами понимают: сложение матриц, умножение матриц на любое действительное число. Для данных операций справедливо 8 аксиом:
1) A+B=B+A
2) A+(B+C)=(A+B)+C
3) A+θ=A
4) A+(-A)= θ
5) 1*A=A
6) 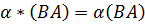
7) α(A+B)=αA+Αb
8) (α+β)A=αA+Βa
Умножение матриц. Для перемножения матриц необходимо чтобы кол-во столбцов у 1й матрицы = кол-ву строк у 2й матрицы. Матрица-строка умножается на матрицу столбец. Свойства умножения матриц:
1)A*B≠B*A 2) A*E(1я матрица)=E*A=A
3)A*(BC)=(AB)*C 4) A*(B+C)=AB+AC
5) (A+B)*C=AC+BC (матрицы умножаются строго по порядку)
Обратные матрицы. Обр. матр. Называется вырожденной, если ее определитель равен 0, в противном случае невырожденной. Если С=AB и определитель С=0, то матрица С-вырожденная и хотя бы одна из А и B тоже вырожденная. B – обратная матрица к А, если справедливо равенство AB=BA=E и обозначается  . Теорема о существовании обратной матрицы. Если матрица А невырожденная, то у нее существует обратная матрица, которая находится по формуле
. Теорема о существовании обратной матрицы. Если матрица А невырожденная, то у нее существует обратная матрица, которая находится по формуле  Матрица
Матрица 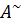 получается из матрицы А заменой каждого элемента матрицы А его алгебраическим дополнением. Теорема о единственности обратной матрицы. Если матрица обратима, то у нее существует только 1 обратная матрица. Док-во: предоложим, что у матрицы А есть 2 обратных матрицы B,C. Тогда т.к. B – обратная к А, следовательно AB=BA=E, но с другой стороны AC=CA=E Рассмотрим матрицу B=BE по 5 свойству умножения матриц B=BE=B(AC)=(BA)C=EC=C,что противоречит свойству, следовательно B=C. Свойства обратных матриц: 1)
получается из матрицы А заменой каждого элемента матрицы А его алгебраическим дополнением. Теорема о единственности обратной матрицы. Если матрица обратима, то у нее существует только 1 обратная матрица. Док-во: предоложим, что у матрицы А есть 2 обратных матрицы B,C. Тогда т.к. B – обратная к А, следовательно AB=BA=E, но с другой стороны AC=CA=E Рассмотрим матрицу B=BE по 5 свойству умножения матриц B=BE=B(AC)=(BA)C=EC=C,что противоречит свойству, следовательно B=C. Свойства обратных матриц: 1)  Док-во:
Док-во:  Докажем, что
Докажем, что  *
*  ‑ обратная к (AB) (AB)(
‑ обратная к (AB) (AB)( )=A(B
)=A(B  )
)  =AE
=AE  =E(
=E( )(AB)=
)(AB)=  (
( A)B=
A)B=  EB=
EB=  B=E Следовательно
B=E Следовательно  – обратная к (AB)
– обратная к (AB)
2)  3) |
3) |  |=
|= 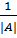 4) определитель транспонированной матрицы
4) определитель транспонированной матрицы  |(
|( )|=
)|= 
6. Элемнтарные преобразования матриц. Приведение к ступенчатому виду.
Эл. Преобразования: 1) перестановка местами любых 2х строк или столбцов матрицы. 2) Умножение любой строки или столбца на любое действ. Число не равное 0. В результате преобразований получается новая матрица эквивалентная данной, причем их определители равны.
Метод гаусса, ранг матрицы. Матрица А порядка MxN называется ступенчатой, если для любых Аij=0 при i>j, для любых i>r, для любых Aii≠0 при i≤r и r≥1, r≤min(m,n) Amxn=  rg=1 Любую прямоугольную матрицу можно привести к ступенчатому виду с помощью элементарных преобразований путем перестановки любых 2х строк, умножения любой строки на число или сложения любых 2х строк. Способ приведения любой прямоугольной матрицы к ступенчатой форме-метод Гаусса.
rg=1 Любую прямоугольную матрицу можно привести к ступенчатому виду с помощью элементарных преобразований путем перестановки любых 2х строк, умножения любой строки на число или сложения любых 2х строк. Способ приведения любой прямоугольной матрицы к ступенчатой форме-метод Гаусса.
7. Пространство 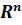 арифметических векторов (линейное пространство).
арифметических векторов (линейное пространство).
Множество элементов x,y,z….  L называется линейным пространством, если для любых элементов x и y из L и для любых α
L называется линейным пространством, если для любых элементов x и y из L и для любых α  R определены операции сложения элементов и умножение элементов на число такие что:
R определены операции сложения элементов и умножение элементов на число такие что:
1) X+Y=Z  L(действит числа) 2) α*X=y
L(действит числа) 2) α*X=y  L Примеры линейных пространств:
L Примеры линейных пространств:
1) Множество действ чисел 2) множество геометрических векторов 3) множество матриц одного порядка 4) множество многочленов какой-либо степени и т.д.
N-мерным арифметическим вектором называется упорядоченная совокупность n-чисел(действит) и записывается  =(x1,x2,…,xn)
=(x1,x2,…,xn)  Для арифметических векторов справедливы операции сложения векторов и умножение вектора на число и аналогичные операции с векторами. Геометрические векторы можно рассматривать, как трехмерные арифметические вектора, а пространство геометрических векторов можно рассматривать, как пространство 3х мерных арифметических векторов.
Для арифметических векторов справедливы операции сложения векторов и умножение вектора на число и аналогичные операции с векторами. Геометрические векторы можно рассматривать, как трехмерные арифметические вектора, а пространство геометрических векторов можно рассматривать, как пространство 3х мерных арифметических векторов.
Рассмотрим линейное пространство L для него справедливы 8 аксиом, удовлетворяющие введенным в пространстве L операций сложения элементов и умножения элементов на число.
1) x+y=y+x 2) x+(y+z)=(x+y)+z 3) x+θ=x 4) 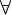 x
x  L,
L, 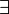 (-x)
(-x)  L 5) 1*x=x 6)
L 5) 1*x=x 6)  7)
7)  Элементы линейного пространства принято называть векторами. Пространство- векторное линейное пространство.
Элементы линейного пространства принято называть векторами. Пространство- векторное линейное пространство.
8. Линейная зависимость. Базис. Линейное пространство в 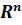 (линейного пространства)
(линейного пространства)
Линейно зависимые и линейно независимые системы векторов. Опр. Система векторов (e1,e2,…ek)  L называется линейно зависимой, если найдутся числа α1,α2,…αk
L называется линейно зависимой, если найдутся числа α1,α2,…αk  R действительные, причем не все равные 0, чтобы выполнялось равенство(α1e1+α2e2+…+αkek=0) Если же данное равенство выполняется, когда α1,α2,…αk=0, тогда система векторов e1,e2,…ek называется линейно независимой. Опр. Если произвольный вектор X из L можно записать в виде равенства x=x1e1+x2e2+…+xken, где Xk
R действительные, причем не все равные 0, чтобы выполнялось равенство(α1e1+α2e2+…+αkek=0) Если же данное равенство выполняется, когда α1,α2,…αk=0, тогда система векторов e1,e2,…ek называется линейно независимой. Опр. Если произвольный вектор X из L можно записать в виде равенства x=x1e1+x2e2+…+xken, где Xk  R то говорят, что x является линейной комбинацией векторов (e1,e2,…ek)
R то говорят, что x является линейной комбинацией векторов (e1,e2,…ek)  L
L
Теорема необходимое и достаточное условие линейной зависимости системы векторов. Для того, чтобы система векторов (e1,e2,…ek)  L была линейно зависимой необходимо и достаточно, чтобы хотя бы 1 из векторов системы можно было бы представить в виде линейной комбинации остальных векторов этой системы. Доказательство. Необходимость. Пусть (e1,e2,…ek) линейно зависимые. Докажем, что при этом хотя бы 1 из векторов можно представить в виде линейной комбинации остальных векторов этой системы. Из определения ЛЗ системы следует что Ǝ α1,α2,…αk
L была линейно зависимой необходимо и достаточно, чтобы хотя бы 1 из векторов системы можно было бы представить в виде линейной комбинации остальных векторов этой системы. Доказательство. Необходимость. Пусть (e1,e2,…ek) линейно зависимые. Докажем, что при этом хотя бы 1 из векторов можно представить в виде линейной комбинации остальных векторов этой системы. Из определения ЛЗ системы следует что Ǝ α1,α2,…αk  R И все α≠0 α1e1+α2e2+…+αkek=0|÷αk, которая не равна 0.
R И все α≠0 α1e1+α2e2+…+αkek=0|÷αk, которая не равна 0.  Достаточность: Пусть 1 из векоров системы можно представить в виде лин. Комбинации остальных векторов системы. Тогда докажем, что система линейно зависимая. Пусть для определения ek является линейной комбинацией остальных векторов системы. Тогда для него найдутся числа
Достаточность: Пусть 1 из векоров системы можно представить в виде лин. Комбинации остальных векторов системы. Тогда докажем, что система линейно зависимая. Пусть для определения ek является линейной комбинацией остальных векторов системы. Тогда для него найдутся числа  ek=
ek= 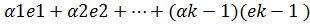
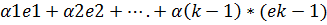 + (‑ 1)*ek=
+ (‑ 1)*ek= 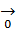 А значит αk=-1≠0 А это значит, что не все α1, α2, αk равны 0. Это значит что система линейно зависимая ч.т.д.
А значит αk=-1≠0 А это значит, что не все α1, α2, αk равны 0. Это значит что система линейно зависимая ч.т.д.
Свойства линейно зависимых и линейно независимых систем векторов:
1) Любая система содержащая 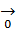 линейно зависимая. 2) любая система содержащая 2 равных вектора линейно зависимая. 3) Любая система, содержащая 2 взаимно противоположных вектора линейно зависимая.
линейно зависимая. 2) любая система содержащая 2 равных вектора линейно зависимая. 3) Любая система, содержащая 2 взаимно противоположных вектора линейно зависимая.
Базис линейного пространства. Опред. Линейное пространство L называется n-мерным, если в нем существует линейно-независимые системы n векторов, а любая система состоящая из n+1 вектора линейно зависимая. В этом случае число n называется размерностью линейного пространства L и обозначается dimL=n или  . Базисом линейного пространства L называется любая система из n линейно-независимых векторов пространства L, причем любой вектор x принадлежащий пространству L может быть представлен в виде линейной комбинации базисных векторов, т.е. если система векторов (e1,e2,…,en) из L образует базис пространства L, то любой вектор x из L можно представить в виде
. Базисом линейного пространства L называется любая система из n линейно-независимых векторов пространства L, причем любой вектор x принадлежащий пространству L может быть представлен в виде линейной комбинации базисных векторов, т.е. если система векторов (e1,e2,…,en) из L образует базис пространства L, то любой вектор x из L можно представить в виде  =α1e1+ α2e2+ α3e3+….+ αnen ‑‑‑‑‑‑ является разложение вектора x по базису e1,e2,en, а действительные числа α1, α2,… αn называются координатами вектора x в базисе e1,e2,….,en.
=α1e1+ α2e2+ α3e3+….+ αnen ‑‑‑‑‑‑ является разложение вектора x по базису e1,e2,en, а действительные числа α1, α2,… αn называются координатами вектора x в базисе e1,e2,….,en.
Теорема в n мерном пространстве L существует базис из n векторов. Без док-ва. Рассмотрим арифметическое пространство 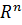 e1(1,0,0,…,0) e2 (0,1,0,…0) e3 (0,0,1,..,0) en (0,0,0,…,0,1) Данная система линейно независимая, т.к. чтобы α1e1+ α2e2+ α3e3=0 равенство выполнялось каждое α должно быть равно 0. Причем любой вектор x принадлежащий пространству
e1(1,0,0,…,0) e2 (0,1,0,…0) e3 (0,0,1,..,0) en (0,0,0,…,0,1) Данная система линейно независимая, т.к. чтобы α1e1+ α2e2+ α3e3=0 равенство выполнялось каждое α должно быть равно 0. Причем любой вектор x принадлежащий пространству 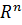 можно представить в виде линейной комбинации (e1,e2,…,en) т.к. вектор x=(x1,x2,x3…xn)=(x1e1,x2e2,x3e3,…,xnen) из определения операций сложения векторов и умножения вектора на число. Поэтому система векторов e1,e2,…,en образует базис в пространстве en, который будем называть естественным базисом пространства
можно представить в виде линейной комбинации (e1,e2,…,en) т.к. вектор x=(x1,x2,x3…xn)=(x1e1,x2e2,x3e3,…,xnen) из определения операций сложения векторов и умножения вектора на число. Поэтому система векторов e1,e2,…,en образует базис в пространстве en, который будем называть естественным базисом пространства 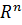 , а действительные числа x1,x2,…,xn координатами вектора x в естественном базисе.
, а действительные числа x1,x2,…,xn координатами вектора x в естественном базисе.
Теорема о единственности разложения вектора по базису. Если система векторов e1,e2,…,en образует базис в пространстве 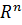 может быть единственным образом представлен в виде x=(c1e1+c2e2+c3e3..+..cnen) где все с принадлежат R. Док-во от противного. Пусть существует 2 различных вектора x по базису en. x =(c1e1+c2e2+c3e3..+..cnen) x=(b1e1+b2e2+b3e3..+..bnen) bi=ci Причем все Сn=Bn, Приравниваем уравнения и получается (c1-b1)e1+(c2-b2)+..+(cn-bn)en=вектор 0. Но т.к. система векторов en образует базис в системе векторов то по определению базиса en, система линейно независимая следовательно равенство выполняется только тогда, когда система линейно зависимая, следовательно разложение вектора по базису единственно. Ч.т.д.
может быть единственным образом представлен в виде x=(c1e1+c2e2+c3e3..+..cnen) где все с принадлежат R. Док-во от противного. Пусть существует 2 различных вектора x по базису en. x =(c1e1+c2e2+c3e3..+..cnen) x=(b1e1+b2e2+b3e3..+..bnen) bi=ci Причем все Сn=Bn, Приравниваем уравнения и получается (c1-b1)e1+(c2-b2)+..+(cn-bn)en=вектор 0. Но т.к. система векторов en образует базис в системе векторов то по определению базиса en, система линейно независимая следовательно равенство выполняется только тогда, когда система линейно зависимая, следовательно разложение вектора по базису единственно. Ч.т.д.
Подпространство линейного пространства  Множество L элементов из
Множество L элементов из 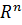 называется линейным подпространством линейного пространства
называется линейным подпространством линейного пространства 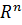 , если для любых векторов x,y
, если для любых векторов x,y  L и для любых α
L и для любых α  R выполняется условие 1) x+y
R выполняется условие 1) x+y  L 2)αx≤L Другими словами множество L из
L 2)αx≤L Другими словами множество L из 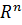 является линейным подпространством линейного пространства L, если множество L само является линейным пространством, относительно лин. Операций введенных в линейном пространстве
является линейным подпространством линейного пространства L, если множество L само является линейным пространством, относительно лин. Операций введенных в линейном пространстве 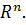 Пример. Рассмотрим множество L, арифметических векторов пространства
Пример. Рассмотрим множество L, арифметических векторов пространства 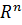 таких, что последняя координата векторов равна 0. Для любых x(x1,x2,…,xn-1,0)
таких, что последняя координата векторов равна 0. Для любых x(x1,x2,…,xn-1,0)  L
L 
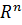 . Для любых x,y
. Для любых x,y  L и для любых α
L и для любых α  R. 1) x+y=(x1+y1,x2+y2,…,xn-1+yn-1,0) 2)αx=(αx1, αx2,…, αxn-1,0)
R. 1) x+y=(x1+y1,x2+y2,…,xn-1+yn-1,0) 2)αx=(αx1, αx2,…, αxn-1,0)  L Следовательно L-лин. Подпространство линейного пространства
L Следовательно L-лин. Подпространство линейного пространства 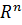 . Линейное пространство
. Линейное пространство 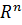 само является линейным подпространством линейного пространства
само является линейным подпространством линейного пространства 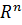 .
.



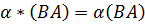
 . Теорема о существовании обратной матрицы. Если матрица А невырожденная, то у нее существует обратная матрица, которая находится по формуле
. Теорема о существовании обратной матрицы. Если матрица А невырожденная, то у нее существует обратная матрица, которая находится по формуле  Матрица
Матрица 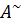 получается из матрицы А заменой каждого элемента матрицы А его алгебраическим дополнением. Теорема о единственности обратной матрицы. Если матрица обратима, то у нее существует только 1 обратная матрица. Док-во: предоложим, что у матрицы А есть 2 обратных матрицы B,C. Тогда т.к. B – обратная к А, следовательно AB=BA=E, но с другой стороны AC=CA=E Рассмотрим матрицу B=BE по 5 свойству умножения матриц B=BE=B(AC)=(BA)C=EC=C,что противоречит свойству, следовательно B=C. Свойства обратных матриц: 1)
получается из матрицы А заменой каждого элемента матрицы А его алгебраическим дополнением. Теорема о единственности обратной матрицы. Если матрица обратима, то у нее существует только 1 обратная матрица. Док-во: предоложим, что у матрицы А есть 2 обратных матрицы B,C. Тогда т.к. B – обратная к А, следовательно AB=BA=E, но с другой стороны AC=CA=E Рассмотрим матрицу B=BE по 5 свойству умножения матриц B=BE=B(AC)=(BA)C=EC=C,что противоречит свойству, следовательно B=C. Свойства обратных матриц: 1)  Док-во:
Док-во:  Докажем, что
Докажем, что  *
*  ‑ обратная к (AB) (AB)(
‑ обратная к (AB) (AB)( )=A(B
)=A(B  )
)  =AE
=AE  =E(
=E( )(AB)=
)(AB)=  3) |
3) | 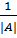 4) определитель транспонированной матрицы
4) определитель транспонированной матрицы  |(
|( )|=
)|= 
 rg=1 Любую прямоугольную матрицу можно привести к ступенчатому виду с помощью элементарных преобразований путем перестановки любых 2х строк, умножения любой строки на число или сложения любых 2х строк. Способ приведения любой прямоугольной матрицы к ступенчатой форме-метод Гаусса.
rg=1 Любую прямоугольную матрицу можно привести к ступенчатому виду с помощью элементарных преобразований путем перестановки любых 2х строк, умножения любой строки на число или сложения любых 2х строк. Способ приведения любой прямоугольной матрицы к ступенчатой форме-метод Гаусса.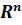 арифметических векторов (линейное пространство).
арифметических векторов (линейное пространство). L называется линейным пространством, если для любых элементов x и y из L и для любых α
L называется линейным пространством, если для любых элементов x и y из L и для любых α  =(x1,x2,…,xn)
=(x1,x2,…,xn)  Для арифметических векторов справедливы операции сложения векторов и умножение вектора на число и аналогичные операции с векторами. Геометрические векторы можно рассматривать, как трехмерные арифметические вектора, а пространство геометрических векторов можно рассматривать, как пространство 3х мерных арифметических векторов.
Для арифметических векторов справедливы операции сложения векторов и умножение вектора на число и аналогичные операции с векторами. Геометрические векторы можно рассматривать, как трехмерные арифметические вектора, а пространство геометрических векторов можно рассматривать, как пространство 3х мерных арифметических векторов.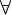 x
x 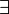 (-x)
(-x)  7)
7)  Элементы линейного пространства принято называть векторами. Пространство- векторное линейное пространство.
Элементы линейного пространства принято называть векторами. Пространство- векторное линейное пространство. Достаточность: Пусть 1 из векоров системы можно представить в виде лин. Комбинации остальных векторов системы. Тогда докажем, что система линейно зависимая. Пусть для определения ek является линейной комбинацией остальных векторов системы. Тогда для него найдутся числа
Достаточность: Пусть 1 из векоров системы можно представить в виде лин. Комбинации остальных векторов системы. Тогда докажем, что система линейно зависимая. Пусть для определения ek является линейной комбинацией остальных векторов системы. Тогда для него найдутся числа  ek=
ek= 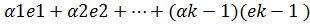
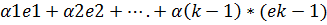 + (‑ 1)*ek=
+ (‑ 1)*ek= 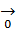 А значит αk=-1≠0 А это значит, что не все α1, α2, αk равны 0. Это значит что система линейно зависимая ч.т.д.
А значит αk=-1≠0 А это значит, что не все α1, α2, αk равны 0. Это значит что система линейно зависимая ч.т.д. . Базисом линейного пространства L называется любая система из n линейно-независимых векторов пространства L, причем любой вектор x принадлежащий пространству L может быть представлен в виде линейной комбинации базисных векторов, т.е. если система векторов (e1,e2,…,en) из L образует базис пространства L, то любой вектор x из L можно представить в виде
. Базисом линейного пространства L называется любая система из n линейно-независимых векторов пространства L, причем любой вектор x принадлежащий пространству L может быть представлен в виде линейной комбинации базисных векторов, т.е. если система векторов (e1,e2,…,en) из L образует базис пространства L, то любой вектор x из L можно представить в виде 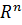 e1(1,0,0,…,0) e2 (0,1,0,…0) e3 (0,0,1,..,0) en (0,0,0,…,0,1) Данная система линейно независимая, т.к. чтобы α1e1+ α2e2+ α3e3=0 равенство выполнялось каждое α должно быть равно 0. Причем любой вектор x принадлежащий пространству
e1(1,0,0,…,0) e2 (0,1,0,…0) e3 (0,0,1,..,0) en (0,0,0,…,0,1) Данная система линейно независимая, т.к. чтобы α1e1+ α2e2+ α3e3=0 равенство выполнялось каждое α должно быть равно 0. Причем любой вектор x принадлежащий пространству  Множество L элементов из
Множество L элементов из 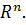 Пример. Рассмотрим множество L, арифметических векторов пространства
Пример. Рассмотрим множество L, арифметических векторов пространства 



