
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выпуклость графика функции. Точки перегиба
Определение. График дифференцируемой функции
На рисунке кривая Теорема. Если вторая производная дважды дифференцируемой функции положительна (отрицательна) внутри некоторого промежутка Х, то функция выпукла вниз (вверх) на этом промежутке. Для нахождения точек перегиба графика функции используется следующая теорема. Теорема (достаточное условие существования точек перегиба). Если вторая производная Схема исследования функции на выпуклость и точки перегиба. 1. Найти вторую производную функции 2. Найти точки, в которых вторая производная 3. Исследовать знак второй производной слева и справа от найденных точек и сделать вывод об интервалах выпуклости и наличии точек перегиба. 4. Найти значения функции в точках перегиба. Асимптоты графика функции Определение.Асимптотой графика функции
Определение. Прямая Определение. Прямая
В частности, если k=0, то Пример. Найти асимптоты для графика функции Решение. 1) Находим вертикальные асимптоты. Точка х=0 – точка разрыва второго рода данной функции, причем
2) Находим горизонтальные асимптоты: 3) Находим наклонные асимптоты:
Следовательно, прямая у=х+2 является наклонной асимптотой графика данной функции как при Общая схема исследования функции и Построения графика
При исследовании функций и построения их графиков рекомендуется использовать следующую схему. 1. Найти область определения функции. 2. Найти (если это можно) точки пересечения графика с осями координат. 3. Выяснить, является ли функция четной, нечетной или общего вида. 4. Найти асимптоты графика функции. 5. Найти интервалы монотонности функции. 6. Найти экстремумы функции. 7. Найти интервалы выпуклости и точки перегиба графика функции. 8. На основании проведенного исследования построить график функции. Если всех пунктов не достаточно, то можно дополнительно исследовать функцию на периодичность, построить дополнительно несколько точек графика, выявить другие особенности функции.
КОЛОКВИУМ 3 ТЕМА: ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ Неопределенный интеграл ПЛАН 1. Понятие первообразной функции. 2. Неопределенный интеграл. 3. Основные свойства неопределенного интеграла. 4. Таблица основных интегралов. -1- В дифференциальном исчислении решается задача: по данной функции f(х) найти ее производную (или дифференциал). Интегральное исчисление решает обратную задачу: найти функцию F(x), зная ее производную F'(x) = f(х) (или дифференциал). Восстановление функции по известной производной этой функции – одна из основных задач интегрального исчисления. Искомую функцию F(x) называют первообразной функции f(х). Определение. Функция F(x) называется первообразной для функции f(х) на промежутке Х, если для всех значений х из того промежутка выполняется равенство F'(x) = f(х) (или dF(x)=f(x)dx). Рассмотрим примеры. 1. Первообразной для функции у=х2, 2. Первообразной для функции у=cos x,
Задача отыскания по заданной функции f(х) ее первообразной решается неоднозначно. Дифференцируя, нетрудно убедиться, что функции Аналогично в общем случае, если F(x) – некоторая первообразная для функции f(х), то, поскольку (F(x)+С)'= F'(x)= f(х), функции вида F(x)+С, где С – произвольное число, также является первообразными для f(х). Теорема. Если функция F(x) является первообразнойфункции f(х) на промежутке Х, то множество всех первообразных для f(х) задается формулой F(x)+С, где С – постоянное число (без доказательства). -2- Определение. Множество всех первообразных функций F(x)+С на промежутке Х для функции f(х) называется неопределенным интегралом от функции f(х) и обозначается символом Таким образом, по определению Здесь f(х) – подынтегральная функция,
х – переменная интегрирования, ∫ – знак неопределенного интеграла. Операция нахождения неопределенного интеграла от некоторой функции называется интегрированием этой функции. Геометрически неопределенный интеграл представляет собой семейство «параллельных» кривых у=F(x)+С (каждому числовому значению С соответствует определенная кривая семейства). График каждой первообразной (кривой) называется интегральной кривой.
-3- Из определения неопределенного интеграла вытекают следующие свойства. 1°. Производная неопределенного интеграла равна подынтегральной функции, т.е.
∆ Дифференцируя левую и правую части равенства (1), получаем
2°. Дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е. d ∆ По определению дифференциала и свойству 1 имеем d Благодаря этим свойствам правильность интегрирования проверяется дифференцированием. Например, равенство ∫(3х2+4)dx=х3+4х+С верно, т.к. (х3+4х+С)'=3х2+4. 3°. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е. ∫dF(x)=F(x)+C, (4) где С – произвольное число. ∆ Рассматривая функцию F(x) как первообразную для некоторой функции f(x), можно записать ∫ f(x)dx=F(x)+C и на основании (3) дифференциал неопределенного интеграла f(x)dx=dF(x), откуда ∫dF(x)=∫f(x)dx=F(x)+C. ▲ Сравнивая между собой свойства 2 и 3, можно сказать, что операции нахождения неопределенного интеграла и дифференциала взаимообратны (знаки d и ∫ взаимно уничтожают друг друга, в случае свойства 3 с точностью до постоянного слагаемого). 4°. Постоянный множитель можно выносить за знак интеграла, т.е. ∫ κf(x)dx=κ ∫f(x)dx, (5) где κ – некоторое число отличное от 0. 5°. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, т.е. ∫ (f(x) ± g(x)) dx = ∫f(x)dx ± ∫g(x)dx. (6) 6°. Если F(x) – первообразная для f(x), то
Пример. Найти интеграл Решение.
где -4- Таблица основных интегралов 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Справедливость приведенных формул проверяется непосредственно дифференцированием.
|
||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 333; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.131.178 (0.027 с.) |
 называется выпуклым вниз на интервале
называется выпуклым вниз на интервале  , если он расположен выше любой ее касательной на этом интервале. График функции
, если он расположен выше любой ее касательной на этом интервале. График функции  Определение. Точка графика непрерывной функции
Определение. Точка графика непрерывной функции  , выпукла вниз на интервале
, выпукла вниз на интервале  , точка М
, точка М  - точка перегиба.
- точка перегиба.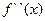 при переходе через точку х0, в которой она равна нулю или не существует, меняет знак, но точка графика с абсциссой х0 есть точка перегиба.
при переходе через точку х0, в которой она равна нулю или не существует, меняет знак, но точка графика с абсциссой х0 есть точка перегиба.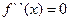 или не существует.
или не существует.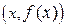 до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.
до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. Асимптоты могут быть вертикальными, наклонными и горизонтальными.
Асимптоты могут быть вертикальными, наклонными и горизонтальными.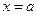 называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции 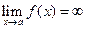 , или
, или 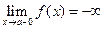 , или
, или 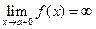 .
.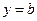 называется горизонтальной асимптотой графика функции
называется горизонтальной асимптотой графика функции 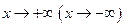 , если
, если 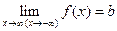 .
. Уравнение наклонной асимптоты будем искать в виде
Уравнение наклонной асимптоты будем искать в виде 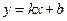 . Если существует наклонная асимптота
. Если существует наклонная асимптота 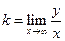 и
и 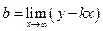 . Если хотя бы один из этих пределов не существует или равен бесконечности, то кривая
. Если хотя бы один из этих пределов не существует или равен бесконечности, то кривая 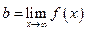 , то получаем уравнение горизонтальной асимптоты.
, то получаем уравнение горизонтальной асимптоты.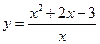 .
. при
при 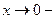 ,
, 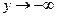 при
при 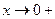 . Следовательно, ось ординат х=0 – вертикальная асимптота.
. Следовательно, ось ординат х=0 – вертикальная асимптота.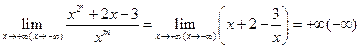 , т.к. n>m. Следовательно, горизонтальных асимптот нет.
, т.к. n>m. Следовательно, горизонтальных асимптот нет.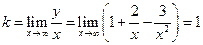 (
(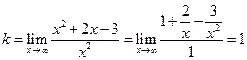 )
)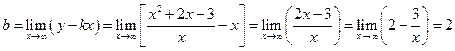 .
.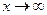 , так и при
, так и при 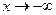 .
.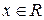 , является функция
, является функция 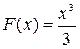 , так как
, так как 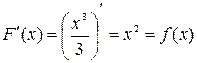 .
.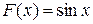 , так как
, так как 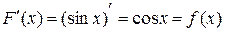 .
.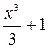 ,
, 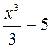 и вообще
и вообще 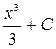 , где С – некоторое число, являются первообразными для функции f(x)= x2.
, где С – некоторое число, являются первообразными для функции f(x)= x2.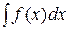 .
.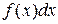 – подынтегральное выражение,
– подынтегральное выражение,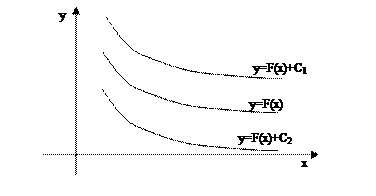
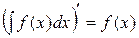 . (2)
. (2)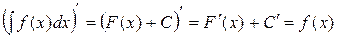 . ▲
. ▲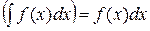 . (3)
. (3)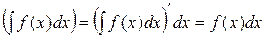 . ▲
. ▲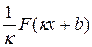 - первообразная для функции f(κx+b), т.е.
- первообразная для функции f(κx+b), т.е.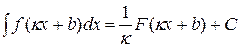 , (κ≠0). (7)
, (κ≠0). (7)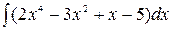 .
.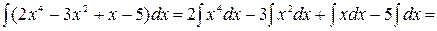
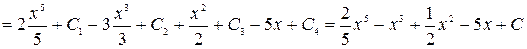 ,
,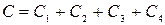 .
. . 11.
. 11. 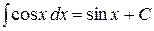 .
.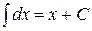 . 12.
. 12. 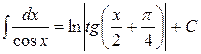 .
.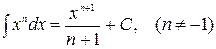 . 13.
. 13. 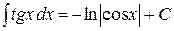 .
.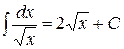 . 14.
. 14. 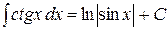 .
.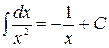 . 15.
. 15. 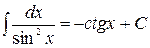 .
. . 16.
. 16. 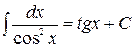 .
.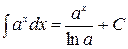 . 17.
. 17. 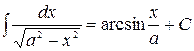 .
.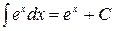 . 18.
. 18. 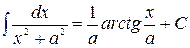 .
.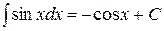 . 19.
. 19. 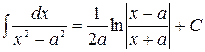 .
.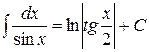 . 20.
. 20. 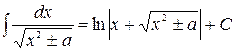 .
.


