
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Система материальных точек. Внутренние и внешние силы. Закон сохранения импульса изолированной системы.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Билет 1. Система материальных точек. Внутренние и внешние силы. Закон сохранения импульса изолированной системы. В любой системе частиц имеется одна замечательная точка, называемая центром масс, которая обладает рядом интересных и важных свойств. Ее положение относительно начала данной системы координат характеризуется радиус-вектором
где
Или
где
Отсюда следует, что центр масс системы материальных точек движется как материальная точка, масса которой равна суммарной массе всей системы, а действующая сила – геометрической сумме всех внешних сил, действующих на все точки системы. Этот результат называется теоремой о движении центра масс системы материальных точек. Уравнение (2.11) по форме совпадает с основным уравнением динамики материальной точки и является его обобщением на систему материальных точек: ускорение системы как целого прямо пропорционально результирующей всех внешних сил и обратно пропорционально суммарной массе системы. Если система замкнута, то Внутренние силы – это силы взаимодействия между частицами системы тел.
Внешние силы – это силы, обусловленные действием других тел, не входящих в систему. По способу приложения они могут быть сосредоточенными и распределенными. Сосредоточенные внешние силы действуют на тело через очень маленькие площадки и с достаточной степенью точности могут считаться приложенными в точке. По характеру действия внешние силы делятся на постоянные и переменные.
Импульс системы может изменяться под действием только внешних сил. Импульс замкнутой системы частиц остается постоянным. Закон сохранения импульса изолированнойсистемы:
Изолированная система – система, состоящая из некоторого количества тел, изолированных от всех остальных тел и образующих механическую систему, т.е. на эти тела не действуют внешние силы, и сами эти тела взаимодействуют друг с другом.
При этом импульсы отдельных частиц или частей замкнутой системы могут меняться со временем. Однако эти изменения всегда происходят так, что приращение импульса одной части системы равно убыли импульса оставшейся части системы.
Внутренние силы – силы, с которыми взаимодействуют тела, составляющие механическую систему.
Импульс изолированной системы сохраняется. Импульсы системы тела – постоянны, если внешние силы отсутствуют.
Билет 2. Работа силы. Связь работы и энергии. Мощность. Закон сохранения механической энергии. Превращение энергии из одного вида в другой. Примеры. Кинетическая энергия поступательного движения. Потенциальная энергия упругого деформированного тела.
Работа силы.
Мощность - величина, характеризующая скорость совершения работы, называется. Мощность численно равна отношению
или в общем случае
Подставляя значение
Частный случай мощности при вращательном движении:
M — момент силы, Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только посредством сил тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком:
По теореме о кинетической энергии эта работа равна изменению кинетической энергии тел:
Следовательно
Билет 3. Билет 4. Абсолютно упругий и абсолютно неупругий удары (столкновения) Превращение энергии в процессе столкновения. Законы сохранения импульса и энергии. Связь между скоростями соударяющихся тел до и после удара. Убыль механической энергии в неупругом ударе. Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения Билет 5. Билет 6. Центр инерции твердого тела. Связь координат и масс твердого тела в системе координат, связанной с центром масс (лемма о центре масс). Координаты центра инерции. Закон движение центра инерции твердого тела.
Если укрепить тело в центре тяжести, то оно будет находиться в равновесии при любом положении тела, т.е. сумма моментов сил тяжести всех частиц тела относительно любой горизонтальной оси, проходящей через центр тяжести, будет равна нулю.
Если повернуть тело относительное оси
а)
б) ex – external – внешний in – internal – внутренний
Центр инерции твердого тела движется так, как если бы к нему были приложены все внешние силы и масса, всего тела была бы сосредоточена в центре масс.
Билет 7. Билет 8. Билет 9. Билет 10. Билет 11. Билет 12. Момент инерции. Вычисление моментов инерции тел (на примере моментов инерции цилиндра, кольца, тонкого кольца, стержня и шара) Чтобы найти момент инерции тела, надо просуммировать момент инерции всех материальных точек, составляющих данное тело Распределение массы в пределах тела можно охарактеризовать с помощью
Пределы интегрирования зависят от формы и размеров тела Интегрирование уравнения (5.5) наиболее просто осуществить для тех случаев, когда ось вращения проходит через центр тяжести тела. Рассмотрим результаты интегрирования для простейших (геометрически правильных) форм твердого тела, масса которого равномерно распределена по объему.
Момент инерции полого цилиндра с тонкими стенками, радиуса R. Для полого цилиндра с тонкими стенками Сплошной однородный диск. Ось вращения является осью диска радиуса Весь диск можно разбить на бесконечное множество цилиндров, а затем просуммировать: Момент инерции шара относительно оси, проходящей через центр тяжести. Момент инерции стержня длиной L и массой m относительно оси, проходящей: а) через центр стержня - б) через начало стержня -
Билет 13. Билет 17. Билет 1. Система материальных точек. Внутренние и внешние силы. Закон сохранения импульса изолированной системы. В любой системе частиц имеется одна замечательная точка, называемая центром масс, которая обладает рядом интересных и важных свойств. Ее положение относительно начала данной системы координат характеризуется радиус-вектором
где
Или
где
Отсюда следует, что центр масс системы материальных точек движется как материальная точка, масса которой равна суммарной массе всей системы, а действующая сила – геометрической сумме всех внешних сил, действующих на все точки системы. Этот результат называется теоремой о движении центра масс системы материальных точек. Уравнение (2.11) по форме совпадает с основным уравнением динамики материальной точки и является его обобщением на систему материальных точек: ускорение системы как целого прямо пропорционально результирующей всех внешних сил и обратно пропорционально суммарной массе системы. Если система замкнута, то Внутренние силы – это силы взаимодействия между частицами системы тел.
Внешние силы – это силы, обусловленные действием других тел, не входящих в систему. По способу приложения они могут быть сосредоточенными и распределенными. Сосредоточенные внешние силы действуют на тело через очень маленькие площадки и с достаточной степенью точности могут считаться приложенными в точке. По характеру действия внешние силы делятся на постоянные и переменные.
Импульс системы может изменяться под действием только внешних сил. Импульс замкнутой системы частиц остается постоянным. Закон сохранения импульса изолированнойсистемы:
Изолированная система – система, состоящая из некоторого количества тел, изолированных от всех остальных тел и образующих механическую систему, т.е. на эти тела не действуют внешние силы, и сами эти тела взаимодействуют друг с другом.
При этом импульсы отдельных частиц или частей замкнутой системы могут меняться со временем. Однако эти изменения всегда происходят так, что приращение импульса одной части системы равно убыли импульса оставшейся части системы.
Внутренние силы – силы, с которыми взаимодействуют тела, составляющие механическую систему.
Импульс изолированной системы сохраняется. Импульсы системы тела – постоянны, если внешние силы отсутствуют.
Билет 2. Работа силы. Связь работы и энергии. Мощность. Закон сохранения механической энергии. Превращение энергии из одного вида в другой. Примеры. Кинетическая энергия поступательного движения. Потенциальная энергия упругого деформированного тела.
Работа силы.
Мощность - величина, характеризующая скорость совершения работы, называется. Мощность численно равна отношению
или в общем случае
Подставляя значение
Частный случай мощности при вращательном движении:
M — момент силы, Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только посредством сил тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком:
По теореме о кинетической энергии эта работа равна изменению кинетической энергии тел:
Следовательно
|
||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 2575; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 , определяемым как
, определяемым как (2.10)
(2.10)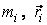 – масса и радиус-вектор
– масса и радиус-вектор  -й частицы,
-й частицы,  – масса всей системы,
– масса всей системы, 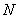 – полное число частиц в системе. Если взять производную по времени от обеих частей уравнения и умножить обе части на
– полное число частиц в системе. Если взять производную по времени от обеих частей уравнения и умножить обе части на  , то получится:
, то получится:
 ,
, – скорость движения центра масс системы. Таким образом, импульс системы материальных точек равен произведению массы системы на скорость ее центра масс:
– скорость движения центра масс системы. Таким образом, импульс системы материальных точек равен произведению массы системы на скорость ее центра масс: .
. (2.11)
(2.11)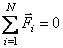 и уравнение (2.11) переходит в
и уравнение (2.11) переходит в  , следовательно,
, следовательно,  . Таким образом, центр масс замкнутой системы движется прямолинейно и равномерно или покоится.
. Таким образом, центр масс замкнутой системы движется прямолинейно и равномерно или покоится.
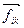 - сила, действующая со стороны тела
- сила, действующая со стороны тела  на
на 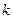
 ,
, 


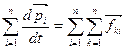






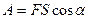








 ,
, 

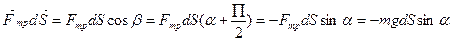



 к промежутку времени
к промежутку времени  за который она совершается.
за который она совершается.
 ,
, получим
получим

 — угловая скорость, n — частота вращения (число оборотов в минуту, об/мин).
— угловая скорость, n — частота вращения (число оборотов в минуту, об/мин).
 или
или
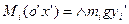
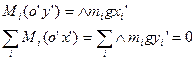
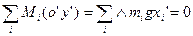
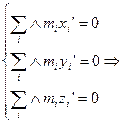
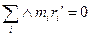 - лемма о центре масс
- лемма о центре масс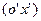 на
на  по часовой стрелке, то ось
по часовой стрелке, то ось 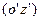 займет положение
займет положение  , и плечом силы тяжести относительно
, и плечом силы тяжести относительно 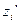 , т.е
, т.е 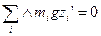
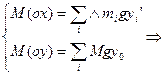

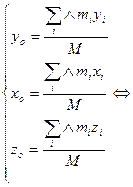
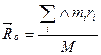
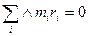 - саму произведения центра масс тела на его радиус-вектор.
- саму произведения центра масс тела на его радиус-вектор.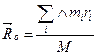
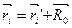
 , (
, (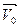 - скорость движения системы отсчета относительно другой.)
- скорость движения системы отсчета относительно другой.)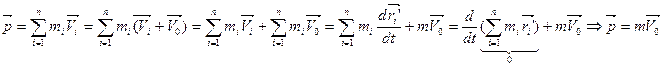 (масса всей системы на скорость центра масс)
(масса всей системы на скорость центра масс)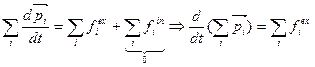

 В общем случае, если тело сплошное, оно представляет собой совокупность множества точек с бесконечно малыми массами
В общем случае, если тело сплошное, оно представляет собой совокупность множества точек с бесконечно малыми массами  , и моменты инерции тела определяется интегралом
, и моменты инерции тела определяется интегралом  где
где  - расстояние от элемента
- расстояние от элемента  где m - масса однородного тела, V - его объем. Для тела с неравномерно распределенной массой это выражение дает среднюю плотность.
где m - масса однородного тела, V - его объем. Для тела с неравномерно распределенной массой это выражение дает среднюю плотность. . Плотность в данной точке в этом случае определяется следующим образом
. Плотность в данной точке в этом случае определяется следующим образом  и тогда
и тогда 

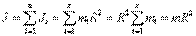
 . и массы m с плотностью
. и массы m с плотностью  Высота диска h. Внутри диска на расстоянии вырежем пустотелый цилиндр с толщиной стенки
Высота диска h. Внутри диска на расстоянии вырежем пустотелый цилиндр с толщиной стенки  и массой
и массой 








