
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Корни n-ой степени из единицы ⇐ ПредыдущаяСтр 6 из 6
рассмотрим z=1+0i . 1+0i=r(cos ϕ +isin ϕ) 1+0i=1(cos 0 + i sin 0) r= cos ϕ=
Теорема. Множество всех комплексных корней n-ой степени из единицы образуют абелевую группу относительно умножения ( Ƹn i =1 i=0;n-1 Ƹ0=Ƹ0 Ƹ1=Ƹ1 Ƹn=Ƹn Ƹ – произвольный корень Ƹ = cos
Кольцо многочлена от одной переменной Рассмотрим некоторое F-коммутативное кольцо с единицей. F – Z,Q,C,R ОПР. Многочленом(полиноном) от переменной х заданным над кольцом F, наз. выражение вида a 0 +a 1 x+a 2 x 2 +…+a n x n, a i f(x)= a 0 +a 1 x+a 2 x 2 +…+a n x n Опр. если a n!=0, a n+1 = 0, a n+2 = 0, то n = deg f(x), a n – старший коэ-т, a 0 – свободный коэ-т. f(x)=0+0x+…+0x n – нулевой многочлен он не имеет степени F[x] – множество всевозможных многочл.над кольцом F Z[x] – целочисленный многочлен На множестве F[x] введем 2 операции, умножение и сложение F 0 (x), g(x) f(x)= a 0 +a 1 x+ …+a n x n g(x)= b 0 +b 1 x +…+b k x k f(x)+g(x) = C 0 +C 1 x+ …+C s x s, где s – максимум из n и k (C0=a0+b0,C1=a1+b1 …Ci=ai+bi) f(x)*g(x)=d0+d1x+…+dmxm, где m - сумма k и n; d i = операция сложения – приведение подобных операция умножения – раскрытие скобок, прив. подобных deg(f(x) + g(x)) ≤ max {deg f(x), deg g(x)} deg (f(x) * g(x))≤ deg f(x) * deg g(x) ТЕОРЕМА. Множество F[x] является коммутативным кольцом с единицей относительно операции сложения и умножения многочленов
81°. Теорема о делении с остатком в кольце многочленов. Теорема. пусть f(x) и g(x) – некоторые многочлены, тогда существуют многочлены q(x) и r(x) F[x], что f(x) = g(x)*q(x)+ r(x), r(x) степень меньше чем g(x) или r(x) = 0 данное представление единственно Док-во: 1) deg f(x)<deg f(x), то f(x)=g(x)*0+f(x) 2) deg f(x)≥deg g(x) f(x)=f(x)-- если k<m, то f(x)= если k≥m, то продолжая аналогично. Мы найдем f i (x) степень которого меньше fi(x)=r(x). Пусть f(x)=g(x)*q(x)+r(x), f 1 (x)=g(x)* f(x)-f 1 (x)=g(x)(q(x)- g(x)(q(x)-
Наибольший общий делитель многочленов. Взаимно простые многочлены. Алгоритм Евклида. Опр. Пусть f(x),g(x)ϵF[x] при чем степень многочлена deg f(x)≥ deg(x), f(x) Св-ва.
Опр. Многочлен кот.явл.делителем 2 других многочленов наз. Их общих делителем. Опр. Наибольшим общим делителем f(x) и g(x) наз. Их общий делитель кот. Делится на все остальные их общие делители. Нод определен с точностью до числового множества. Нод(f(x),g(x))=d(x)
Опр. Многочлены наз. Взаимно простыми., если НОД их явл. Многоченом нулевой степени Теорема. Если f(x)=g(x)*q(x)+r(x), то НОД многочлен f(x),g(x), такой же НОД(g(x),f(x)). АЛГОРИТМ ЕВКЛИДА Найти НОД (f(x),g(x)). Пусть Deg f(x) ≥ deg g(x), если f(x) g(x)=r1(x)*q2(x)+r2(x), если r2!=0, то r1(x)=r2(x)*q3(x)+r3(x)… rn-1=rn(x)*qn+1(x) теорема. Если d(x)=НОД(f(x),g(x))
Критерий взаимнопростые многочлены:f(x) и g(x)-взаимопростые
Разложение многочлена на неприводимые многочлены. Пусть f(x) многочлен из F[x], F – поле, многочлен f(x) наз-ся неприводимым над полем F, если он не имеет делителей кроме делителей нулевой степени(α и αf(x)). В противоположном случае многочлен называется приводимым. Св-ва неприводимого мн-чл. 1)Если f(x) – неприводим, а α – элемент поля, α!=0, то α(f(x)) - неприводим 2)Многочлен 1-ой степени над любым полем неприводим 3)Если f(x) – неприводим, g(x) – произвольный мн/чл., то либо g(x) ТЕОРЕМА Всякий многочлен можно представить в виде произведения неприводимого многочлена, причем данное разложение единственно с точностью до числового множителя и порядка следования множителей.
84°. Корни многочлена от одной переменной. Схема Горнера. Пусть ОПР. Элемент С взятый из поля F, называется корнем многочлена f(x) Теорма Безу: Элемент С явл. Корнем f(x), тогда и тока тогда, когда
СХЕМА ГОРНЕРА q(x)=b0xn-1 + b1xn-2 +…+ bn-2x + bn-1
Опр. Пусть с-корень f(x). C-наз.K- Кратным корнем f(x), если Теорема. Многочлен в степени n имеет n-корень, при этом если многочлен разложен на первую степень, то он имеет n-четное кол-во корней.
Интерполяционный многочлен Лагранжа. ТЕОРЕМА Для любого натур числа n существует единственный многочлен степени ≤n, который принимает на перед заданные значения для n+первого значения переменной Д-ВО: Пусть многочлен f(x)
f(a0)=b0,…, f(an)=bn f(x) = . f(a0)=
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1747; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.229.113 (0.023 с.) |

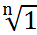
 r=
r= 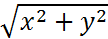
 sin ϕ =
sin ϕ =  ϕ=0;
ϕ=0; =
=  =
= 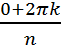 + I
+ I 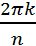 + i sin
+ i sin 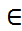 0;n-1.
0;n-1. = cos
= cos  + I sin
+ I sin  ,Ƹ0,Ƹ1,Ƹ2,…, Ƹn)
,Ƹ0,Ƹ1,Ƹ2,…, Ƹn) + i sin
+ i sin 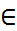 F[x]
F[x] j b t
j b t если m<n
если m<n
 , где s<x
, где s<x ;
; )+(r(x)-
)+(r(x)- 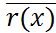 )
) g(x), если сущ. ϕ (x), это f(x)=g(x).
g(x), если сущ. ϕ (x), это f(x)=g(x).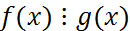 , если r(x)=0
, если r(x)=0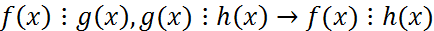
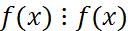
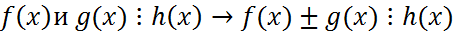
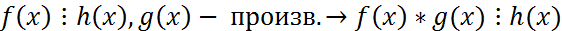
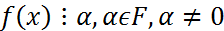
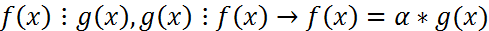
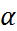 .
.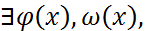
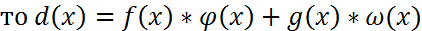
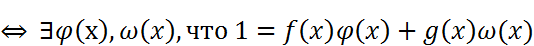
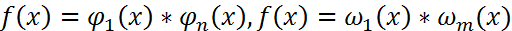
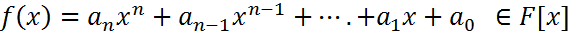 F-поле, С-элемент поля, тогда F(C)=
F-поле, С-элемент поля, тогда F(C)= 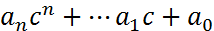 -значение многочлена при x=c.
-значение многочлена при x=c.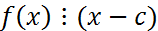
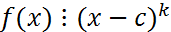 , но не делится на
, но не делится на 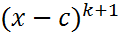 .
. j
j  j(x)
j(x)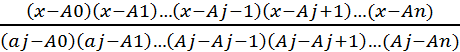 ;
;


