
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неравенство и теорема Чебышева
Неравенство Чебышева. Вероятность того, что отклонение случайной величины от ее математического ожидания по модулю меньше числа Рассмотрим дискретную случайную величину X, имеющую закон распределения:
Закон распределения случайной величины
Предположим, что первые k значений случайной величины Теорема Чебышева. Если Рассмотрим случайную величину
Теорема Бернулли Пусть в каждом из n независимых испытаний вероятность p появления события А постоянна. Тогда как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности p по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико. Или Пусть Теорема Пуассона. Если в последовательности n независимых испытаний вероятность появления события А в каждом испытании равна Пусть случайная величина
Функция одного случайного аргумента и ее распределение
Если каждому возможному значения случайной величины Х соответствует одно возможное значение случайной величины Y, то Y – функция от X: Y=j(X). Найдем закон распределения вероятностей функции по известному распределению дискретного и непрерывного аргумента. 1) Если X – дискретная величина. Найти распределение Y=X2. Вероятности соответствующих значений X и Y равны:
2) Пусть X – непрерывная случайная величина. Пусть Y=j(X) и плотность распределения f(x) известна, тогда
Математическое ожидание функции одного случайного аргумента
Пусть Y=j (X) – функция случайного аргумента Х. Найдем M (Y). Пусть Х дискретная случайная величина: Пусть X – непрерывная случайная величина, заданная плотностью f (x). а) можно найти g (y) – плотность распределения величины Y и
Закон распределения вероятностей и функция распределения двумерных случайных величин
До сих пор мы рассматривали случайные величины, возможные значения которых определялись одним числом – одномерные. Кроме одномерных случайных величин изучают величины, возможные значения которых определяются 2, 3,…, n числами. Такие величины называются двумерными, трехмерными, …, n -мерными. Будем обозначать через (X, Y) двумерную случайную величину. Каждую из величин X, Y называют компонентами (составляющими); обе величины X и Y, рассматриваемые одновременно, образуют систему двух случайных величин. Пример: станок штампует плитки. Если контролировать длину X и ширину Y – то имеем двухмерную случайную величину (X, Y).
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 248; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.105.239 (0.007 с.) |
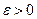 , не меньше, чем
, не меньше, чем 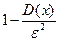 , т.е.
, т.е. 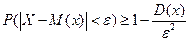 .
.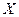

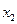

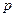
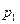

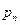
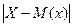 :
: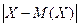
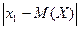
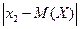
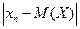
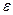 . Тогда
. Тогда 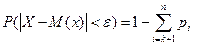 . Запишем формулу для дисперсии в виде:
. Запишем формулу для дисперсии в виде: 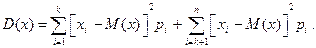 Отбросим первое слагаемое и во втором слагаемом заменим
Отбросим первое слагаемое и во втором слагаемом заменим 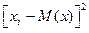 меньшей величиной
меньшей величиной 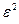 , получим
, получим 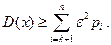 Отсюда:
Отсюда: 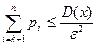 , т.е.
, т.е. 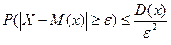 . Для частости:
. Для частости:  .
.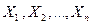 - попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышают постоянного числа С), то, как бы мало ни было
- попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышают постоянного числа С), то, как бы мало ни было 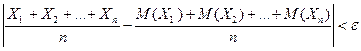 будет как угодно близка к единице, если число случайных величин достаточно велико, т.е.
будет как угодно близка к единице, если число случайных величин достаточно велико, т.е. 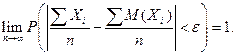
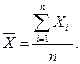 Имеем:
Имеем: 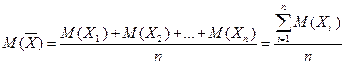 ;
; 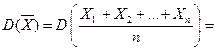
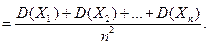 По условию теоремы дисперсия ограничена, т.е.
По условию теоремы дисперсия ограничена, т.е. 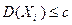 , поэтому
, поэтому 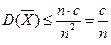 . Воспользуемся неравенством Чебышева:
. Воспользуемся неравенством Чебышева: 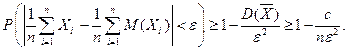 Перейдя к пределу и учитывая, что
Перейдя к пределу и учитывая, что 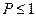 , получим доказываемое.
, получим доказываемое. , где
, где 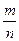 – частота появления события A.
– частота появления события A.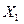 – число появлений события A в первом испытании,
– число появлений события A в первом испытании, 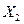 – во втором,
– во втором,  – в n -ом испытании,
– в n -ом испытании, 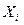 может принимать значения: 1 (событие А наступило) с вероятность р и 0 (событие А не наступило) с вероятностью
может принимать значения: 1 (событие А наступило) с вероятность р и 0 (событие А не наступило) с вероятностью 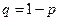 . Испытания независимые,
. Испытания независимые, 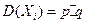 , так как
, так как 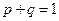 , то
, то 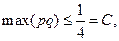
 , тогда по неравенству Чебышева:
, тогда по неравенству Чебышева: 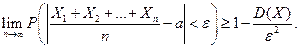
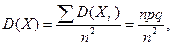
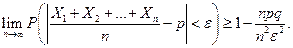 Каждая величина
Каждая величина 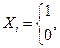 тогда
тогда 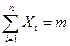 – числу появления события А в n испытаниях, тогда
– числу появления события А в n испытаниях, тогда 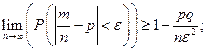 следовательно,
следовательно, 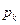 , то при увеличении n частость события A сходится (по вероятности) к среднему арифметическому вероятностей
, то при увеличении n частость события A сходится (по вероятности) к среднему арифметическому вероятностей 
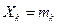 – число появлений события А в каждом испытании, тогда
– число появлений события А в каждом испытании, тогда 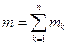 – число появлений события А в n испытаниях.
– число появлений события А в n испытаниях. 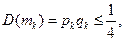
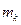 – независимые величины. Для случайной величины
– независимые величины. Для случайной величины 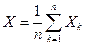 имеем:
имеем: 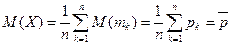 среднее арифметическое вероятностей;
среднее арифметическое вероятностей; 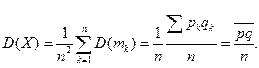 Тогда по неравенству Чебышева:
Тогда по неравенству Чебышева: 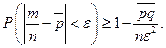 Переходя к пределу, получим доказываемое.
Переходя к пределу, получим доказываемое.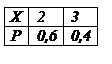
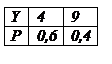
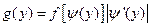 , где
, где 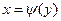 – обратная функция для функции у=j (х), которая должна быть дифференцируемой и строго возрастающей или убывающей функцией.
– обратная функция для функции у=j (х), которая должна быть дифференцируемой и строго возрастающей или убывающей функцией.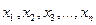 с вероятностью
с вероятностью 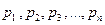 , Y – тоже дискретная случайная величина со значениями:
, Y – тоже дискретная случайная величина со значениями: 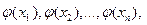 с вероятностью
с вероятностью 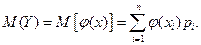
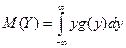 , однако проще:
, однако проще: 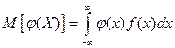 .
.


