
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Среднее квадратичное отклонение. Начальные и центральные теоретические моменты
Среднее квадратичное отклонение случайной величины Х – это корень квадратный из дисперсии: Размерность дисперсии равна квадрату размерности Х, тогда как размерность s(Х) равна размерности Х. Во многих случаях это оказывается удобнее. Пусть
Начальные и центральные теоретические моменты Начальным моментом порядка k случайной величины Х называют математическое ожидание величины
Центральным моментом порядка k называется математическое ожидание величины Мода и медиана. Модой Медианой
Функция распределения вероятностей случайной величины
Дискретная случайная величина может быть задана перечислением всех ее возможных значений и их вероятностей – законом распределения. Но его нельзя использовать для задания непрерывных случайных величин. Необходим общий способ задания случайных величин - это функция распределения вероятностей случайных величин. Пусть x – действительное число. Вероятность того, что случайная величина Х примет значение, меньше x, т.е. Р (X<x) обозначим через F (x). Если x изменяется, то изменяется и F (x), т.е. F (x) – функция х. Функцией распределения называют функцию F (x), определяющую вероятность того, что случайная величина Х в результате испытания примет значение, меньше x, т.е. F (x)= P (X<x). Геометрически F (x) есть вероятность того, что случайная величина примет значение, которое изображается точкой левее точки х. Добавим более четкое определение непрерывной случайной величины – случайная величина называется непрерывной, если ее функция распределения есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.
Свойства F (x) 1. Значения функции распределения принадлежат отрезку [0;1], т.е. 0 £ F (x)£ 1 – F (x) вероятность, 0 £ P (A) £ 1.
2. F (x) неубывающая функция, т.е. F ( Доказательство: Пусть 1. Х примет значение, меньше 2. Х примет значение По теореме сложения: Р ( отсюда Р ( Следствие 1. Вероятность того, что Следствие 2. Вероятность того, что случайная величина Х примет одно определенное значение равна 0. Р (a £ Х < b) = Р (a < Х < b) = Р (a < x £ b) = Р (a £ x £ b). 3. Если возможные значения случайной величины Î (a, b), то: 1) F (x)= 0 при x £ a; 2) F (x) = 1 при x >b. Докажем. Если Следствие. Если значения непрерывной случайной величины расположены на всей числовой оси, то
Плотность распределения вероятностей непрерывной Случайной величины Непрерывную случайную величину можно задать функцией распределения, однако можно использовать и плотностью распределения. Плотностью распределения вероятностей непрерывной случайной величины Х называют производную от функции распределения: Для описания распределения вероятностей дискретной случайной величины плотность распределения неприменима. Теорема. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a,b), равно Доказательство: Если известна функция распределения, то Р (a £ X £ b) = F (b) – F (a). По формуле Ньютона-Лейбница: F (b) – F (a) = Пример. Дана плотность вероятности:
Найти вероятность того, что в результате испытания Х примет значение Î (0,5; 1). Р (0,5 < X < 1) = Функцию распределения можно найти по плотности распределения: F (x) = По известной функции распределения можно найти плотность: Пример. Найти F(x), если Если x £ a, f (x) = 0, то
Свойства f (x) 1. f (x) ³ 0, т.к. F (x) – неубывающая функция, поэтому, 2. Вероятностный смысл
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 300; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.6.75 (0.012 с.) |
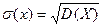 .
.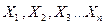 – независимые случайные величины, тогда
– независимые случайные величины, тогда 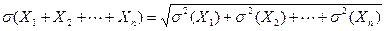 . По свойству дисперсии:
. По свойству дисперсии: 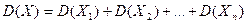 , тогда
, тогда 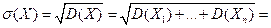
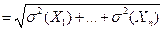 .
.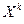 :
:  Например,
Например,  ,
, 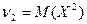 ,
,  ,…
,… .
.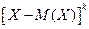 :
: 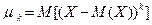 , например,
, например, 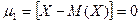 ,
, 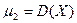 и т.д.
и т.д. случайной величины называется ее наиболее вероятное значение (для дискретных величин) или то значение, в котором плотность вероятности максимальна. Если имеется более одного максимума, то распределение называют полимодальным.
случайной величины называется ее наиболее вероятное значение (для дискретных величин) или то значение, в котором плотность вероятности максимальна. Если имеется более одного максимума, то распределение называют полимодальным.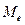 называют такое значение случайной величины (обычно – непрерывной), для которого
называют такое значение случайной величины (обычно – непрерывной), для которого 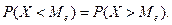 Геометрически – абсцисса точки, в которой площадь делится пополам.
Геометрически – абсцисса точки, в которой площадь делится пополам.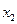 ) ³ F (
) ³ F ( ), если
), если  <
< 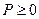 .
.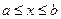 равна приращению F (x) на этом интервале: Р (
равна приращению F (x) на этом интервале: Р (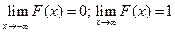 .
.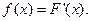
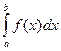 , т.е. Р (a < Х < b) =
, т.е. Р (a < Х < b) = 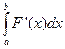 =
= 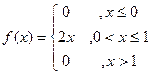 .
.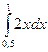 = 0,75.
= 0,75.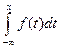 . Действительно, F (x) = P (X < x) или F (x) = P (–¥ < X < x), тогда
. Действительно, F (x) = P (X < x) или F (x) = P (–¥ < X < x), тогда  .
.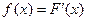 .
.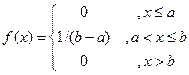 .
. , если
, если 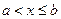 :
: 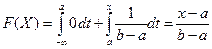 . Если
. Если 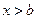 , то
, то 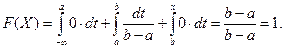
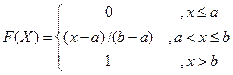 .
.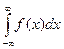 =1. Этот интеграл выражает вероятность события, состоящего в том, что случайная величина примет значение
=1. Этот интеграл выражает вероятность события, состоящего в том, что случайная величина примет значение 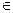 (–µ;µ) – достоверное событие, поэтому р = 1.
(–µ;µ) – достоверное событие, поэтому р = 1.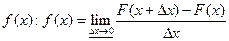 , тогда:
, тогда: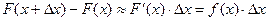 – вероятность того, что случайная величина примет значение
– вероятность того, что случайная величина примет значение 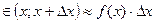 .
.


