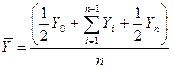Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорія ймовірностей, ймовірнісні процеси і математична статистикаСтр 1 из 5Следующая ⇒
Теорія ймовірностей, ймовірнісні процеси і математична статистика 1. Класичне визначення ймовірності. Эксперимент, исход которого невозможно предсказать, называют случайным экспериментом (СЭ). Событие, которое в данном СЭ может произойти, а может и не произойти, называют случайным событием. Элементарными исходами называют события, удовлетворяющие требованиям: 1. при всякой реализации СЭ происходит один и только один элементарный исход; 2. всякое событие есть некоторая комбинация, некоторый набор элементарных исходов. Множество всех возможных элементарных исходов полностью описывает СЭ. Такое множество принято называть пространством элементарных исходов (ПЭИ). Выбор ПЭИ для описания данного СЭ неоднозначен и зависит от решаемой задачи. Если элементарные исходы СЭ обладают свойством равновозможности (в силу определенной “симметрии” условий), то вероятность Р(А) любого события А определяется формулой: Р(А) = n(A) / n, где n – общее число равновозможных исходов, n(A) – число исходов, составляющих событие А, как говорят еще, благоприятствующих событию А.
Теореми додавання та множення ймовірностей. Сумма событий А и В есть событие А+В, состоящее в наступлении хотя бы одного из событий А или В. Произведение событий А и В есть событие А*В, состоящее в совместном наступлении обоих событий А и В. События называются несовместными, если их совместное наступление невозможно.
Некоторые свойства: Вероятность события А, вычисленная в предположении, что событие В произошло, называется условной вероятностью Р(А/В). События А и В называются независимыми, если Р(А/В) = Р(А) (или Р(В/А) = Р(В)). Теорема умножения 1. (ТУ1): Р(АВ) = Р(А)*Р(В/А) = Р(В)*Р(А/В). ТУ 2.: вероятность совместного наступления независимых событий равна произведению их вероятностей. Теорема сложения 1. (ТС1): вероятность суммы попарно несовместных событий равна сумме их вероятностей.
ТС 3.: Р(А+В) = Р(А) + Р(В) – Р(АВ).
Формула повної ймовірності. Формула Байєса. Теорема. Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий B1, B2,..., Вn, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:
Р (А) = Р (В1) PB1 (А) + Р (В2) PB2 (A) +... + Р(Вn)РBn(А). Эту формулу называют «формулой полной вероятности». Основные определения и формулы: Пусть событие А может произойти только совместно с одним из попарно несовместных событий Н1, Н2, …, Нn (это имеет место, например, для полной группы событий Нк, к = 1.. n). Тогда: Р(А) = Если при этом Р(А) ¹ 0, то Р(Нm/А) = Выбор подходящих гипотез Н1, Н2, …, Нn зависит от того, можем ли мы достаточно просто вычислить условные вероятности Р(А/Нк).
Випадкові величини (ВВ). Дискретні та неперервні ВВ. Случайная величина(СВ) – величина, которая в результате опыта может принять то или иное значение, неизвестно заранее – какое именно. Закон распределения СВ – всякое соотношение, устанавливающее связь между всевозможными значениями СВ и соответствующими вероятностями. Дискретная СВ – случайная величина, множество значений которой конечно или счетное и принимает отдельные, изолированные значения с определенными вероятностями. Задается рядом распределения, многоугольником распределения, функцией распределения. Ряд распределения – таблица, в которой перечислены возможные значения СВ Х и соответствующие им вероятности. Р Многоугольник распределения – Графическое изображение ряда распределения. Непрерывная СВ – случайная величина, которая принимает все значения из некоторого конечного или бесконечного промежутка; непрерывно занимает некоторый промежуток. Задается функцией распределения и функцией плотности. Для НСВ вводятся те же числовые характеристики, что и для ДСВ. В формулах для их вычисления суммы заменяются интегралами, например: М(Х) = причем, требуется, чтобы написанный несобственный интеграл сходился абсолютно. Для НСВ Х вводится еще одна характеристика – медиана Ме(Х) – следующим равенством: Р(Х < Me(X)) = P(X > Me(X)). Распишем функцию от случайной величины.
Пусть НСВ Х и Y связаны функциональной зависимостью Y = j(х), где j(х) – дифференцируемая функция, монотонная на всем интервале возможных значений СВ Х. Тогда, если f (x) – плотность СВ Х, а g(y) – плотность СВ Y, то g(y) = f(y(y))| y’(y)|, где y(y) – функция, обратная по отношению к j(х). Если на интервале возможных значений СВ Х обратная функция y(y) неоднозначна, т.е. одному значению у соответствует несколько значений х: y1(y), y2(y),…, yn(y), то плотность СВ Y определяется формулой:
Распишем функцию от 2-х случайных величин. Для функции нескольких случайных величин удобнее искать функцию распределения, а плотность определять дифференцированием. Если НСВ Z есть функция от двух случайных аргументов Х и Y: Z = j (X, Y), то ее функция распределения имеет вид:
Щільність ймовірностей. Функцией распределения (вероятностей) СВ Х называют функцию F(x): F(x) = Р(Х<х). Функция распределения в точке х равна вероятности того, что СВ Х принимает значение меньше х. Свойства F(x) 1. Функция распределения СВ Х есть неотрицательная функция, заключенная между 0 и 1: 0 2. На минус бесконечности функция распределения = 0: F(- 3. На плюс бесконечности функция распределения =1: F(+ 4. Функция распределения есть неубывающая функция своего аргумента: F(x1) Непрерывная СВ – случайная величина, которая принимает все значения из некоторого конечного или бесконечного промежутка; непрерывно занимает некоторый промежуток. Задается функцией распределения и функцией плотности. Плотностью распределения (плотностью вероятности или просто плотностью) непрерывной СВ называется производная ее функции распределения: 1. Плотность вероятности –неотрицательная функция: f(x) 2. Несобственный интеграл в бесконечных пределах от плотности вероятности НСВ равен 1: 3. Площадь под кривой распределения f(x) равна 1. Для любой СВ: Р(а<X<b)= F(b)-F(a). Для НСВ: P(a<X<b)= Для НСВ вводятся те же числовые характеристики, что и для ДСВ. В формулах для их вычисления суммы заменяются интегралами, например: М(Х) = причем, требуется, чтобы написанный несобственный интеграл сходился абсолютно. Для НСВ Х вводится еще одна характеристика – медиана Ме(Х) – следующим равенством: Р(Х < Me(X)) = P(X > Me(X)). Розподілу. Равномерное распределение - непрерывная величина, принимающая значение из некоторого интервала, ни одно из значений которого не является более вероятным. Функцией плотности распределения непрерывной случайной величины X называют функцию f (х)— первую производную от функции распределения F(х):
Функция распределения случайной величины Х, распределенная по равномерному закону на отрезке [a,b]
M[x] = Математическим ожиданием непрерывной случайной величины X, возможные значения которой принадлежат отрезку [а, b], называют определенный интеграл: Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения. Если возможные значения X принадлежат отрезку [a,b], то:
М (X) = m, т. е. математическое ожидание нормального распределения равно параметру m. Изменение величины параметра m (математического ожидания) не изменяет формы нормальной кривой, а приводит лишь к ее сдвигу вдоль оси Ох: вправо, если m возрастает, и влево, если m убывает. С возрастанием σ максимальная ордината нормальной кривой убывает, а сама кривая становится более пологой, т. е. сжимается к оси Ох; при убывании σ нормальная кривая становится более «островершинной» и растягивается в положительном направлении оси Оу. Функция распределения нормального закона с параметрами N(m,σ) равна
Для нормального распределения матожидание равно моде и медиане Нормально распределенная с параметрами т и s случайная величина практически всегда принимает значения из промежутка (т – 3s; т + 3s).
Функция распределения плотности экспоненциального закона
Вероятность попадания случайной величины в интервал [a,b]:
Способы отбора выборки - Бесповторный отбор (схема невозвращенного шара) – каждый элемент, случайно отобранный из ГС, исследуется и не возвращается назад в ГС. - Повторный отбор (схема возвращенного шара) – каждый элемент, случайно отобранный из ГС, исследуется и возвращается назад в ГС. В качестве модели ГС выбирается выборочная совокупность неограниченного объема. Оценка матожидания Точечная оценка матожидания по вариационному ряду – это среднеарифметическое наблюденных значений: Для других законов: В качестве оценки m по частотно-вариационному ряду принимают средневзвешенную оценку: где xi – вариант, k – количество вариантов в выборке. Для интервального ряда: х` i – середина i-го интервала, mi – количество элементов выборки, попавших в i -тый интервал,
k – количество интервалов. Оценка дисперсии Оценка дисперсии для интервального ряда вычисляется по формуле: Выборочный коэффициент асимметрии по вариационному ряду находится по формуле: Выборочный коэффициент эксцесса для вариационного ряда находится по формуле: Критерии согласия Критерии согласия позволяют отвергнуть или подтвердить правильность выдвинутой при выравнивании ряда гипотезы о характере распределения в эмпирическом ряду. Критерий Пирсона ( χ2 - “хи”-квадрат) Алгоритм применения критерия 1. Определить меру расхождения между теоретическими (npi) и эмпирическими частотами (mi): где F(x) - функция распределения предполагаемого теоретического закона распределения. 2. Для выбранного уровня значимости α по таблице χ2 - распределения, находят критическое значение меры расхождения: где r – число степеней свободы:, r = k- s k – количество интервалов в группировке, s – число налагаемых связей (условий) на частости: s= s`+ 1 где s` - количество параметров предполагаемого теоретического закона распределения, тогда: r = k- s`-1 3. Фактически наблюдаемое значение:. χ 2 сравнивается с критическим значением при Статистика Критерий Колмогорова В качестве меры расхождения между теоретическим и эмпирическим распределением по критерию Колмогорова рассматривается максимальное расхождение между теоретической и эмпирической функциями распределения. D = max|F*(x) – F(x)|, где F*(x) – статистическая функция распределения, получаемая по выборке, F(x) – теоретическая функция распределения, полученная по предложению о законе распределения. 1.Строится эмпирическая функция распределения F*(x) и предполагаемая теоретическая функция F(x). 2.Определяется мера расхождения между теоретическими и эмпирическими значениями функции распределения: Задается уровень значимости, вычисляем критическое значение: λкр = λα 3.Если λ* > λ кр., гипотеза отвергается, если λ* ≤ λ кр, гипотеза не противоречит опытным данным, то есть СВ Х имеет предполагаемый теоретический закон распределения, не противоречащий имеющимся выборочным данным. Кореляційний аналіз даних. Распишем 2-мерную дискретную случайную величину. Если результат СЭ описывается двумя случайными величинами X и Y, то принято говорить о 2-мерной СВ или о системе СВ (Х0Y). Ее интерпретируют как случайную точку с координатами (X; Y) по плоскости хОу или как случайный радиус-вектор такой точки. Совместной функцией распределения системы (Х, Y) называют функцию F(x; y) двух переменных, определяемую равенством: F(x; y) = P{(X < x)*(Y < y)}.
Геометрически F(x; y) представляет собой вероятность попадания случайной точки (х; у) в бесконечный квадрат с вершиной (х; у), лежащий левее и ниже ее. Пусть ДСВ Х и Y принимают значения х1, х2, … и у1, у2, … соответственно. Тогда совместный закон распределения можно задавать матрицей (Рij), элементы которой рij=P{(X = xi)(Y = yj)}, удовлетворяют очевидному условию: Суммируя вероятности рij по строкам, получим ряд распределения СВ Х, а суммируя их по столбцам – СВ Y. Пусть т1 и т2 – математические ожидания, s1 и s2 – средние квадратичные отклонения случайных величин Х и Y соответственно. Коэффициентом корреляции системы (X; Y)называют число: Свойства коэффициента корреляции: 1. –1 £ r £ 1; 2. если X и Y – независимы, то r = 0; 3. если Y = aX + b, где a и b - неслучайны, то r = ±1 (знак “+” соответствует а > 0, знак “–” соответствует а < 0). Часові ряди. Ряд динамики, или временной ряд – последовательность упорядоченных во времени числовых показателей, характеризующих уровень развития изучаемого явления. Каждое конкретное значение называется уровнем ряда. Интервальный динамический ряд характеризуется последовательностью, когда уровни ряда относятся к результату, накопленному или произведенному за определенный интервал времени (ряды объемов продукции по месяцам года, объемы перевозок за недели, месяцы или кварталы, экономические показатели предприятий по отдельным периодам и т.д.). Моментный динамический ряд характеризуется последовательностью, когда уровни ряда показывают фактическое наличие изучаемого явления на конкретный момент времени (ряды численности населения на начало года, величины запасов сырья на начало периода и т.д.). Комплексные ряды - отображают динамику совокупности нескольких разных показателей во времени. Цели анализа временных рядов направлены на определение природы ряда или его прогнозирование (предсказание будущих значений временного ряда по настоящим и прошлым значениям). Показатели, исчисляемые как отношение уровня ряда в данный момент или интервал времени к непосредственно предшествующему уровню, называются цепными, т.е. цепные коэффициенты (темпы) роста равны Абсолютный прирост – разность двух уровней ряда динамики. Цепной абсолютный прирост исчисляется как разность между сравниваемым уровнем Темп прироста – это абсолютный прирост в относительных величинах. Цепной темп прироста представляет собой отношение сравниваемого цепного абсолютного прироста Средний уровень ряда – показатель, обобщающий итоги развития явления за определенный интервал из имеющейся временной последовательности. Для интервальных временных рядов с равными периодами времени средний уровень равен:
Для моментных временных рядов при условии, что в пределах каждого периода развитие происходило по линейному закону, средний уровень (среднее хронологическое) равен: Многие монотонные временные ряды можно хорошо приблизить линейной функцией. Если же имеется явная монотонная нелинейная компонента, то данные вначале следует преобразовать, чтобы устранить нелинейность. Обычно для этого используют логарифмическое, экспоненциальное или (менее часто) полиномиальное преобразование данных. Теорія ймовірностей, ймовірнісні процеси і математична статистика 1. Класичне визначення ймовірності. Эксперимент, исход которого невозможно предсказать, называют случайным экспериментом (СЭ). Событие, которое в данном СЭ может произойти, а может и не произойти, называют случайным событием. Элементарными исходами называют события, удовлетворяющие требованиям: 1. при всякой реализации СЭ происходит один и только один элементарный исход; 2. всякое событие есть некоторая комбинация, некоторый набор элементарных исходов. Множество всех возможных элементарных исходов полностью описывает СЭ. Такое множество принято называть пространством элементарных исходов (ПЭИ). Выбор ПЭИ для описания данного СЭ неоднозначен и зависит от решаемой задачи. Если элементарные исходы СЭ обладают свойством равновозможности (в силу определенной “симметрии” условий), то вероятность Р(А) любого события А определяется формулой: Р(А) = n(A) / n, где n – общее число равновозможных исходов, n(A) – число исходов, составляющих событие А, как говорят еще, благоприятствующих событию А.
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 163; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.136.235 (0.093 с.) |

 Противоположное событие для события А есть событие А, состоящее в ненаступлении события А. События А и А – несовместны, а их сумма совпадает с ПЭИ.
Противоположное событие для события А есть событие А, состоящее в ненаступлении события А. События А и А – несовместны, а их сумма совпадает с ПЭИ.
 ТС 2.: Р(А) = 1 – Р(А).
ТС 2.: Р(А) = 1 – Р(А).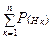 Р(А/Нк). (формула полной вероятности).
Р(А/Нк). (формула полной вероятности).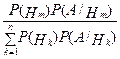 , m = 1.. n. (формула Байеса).
, m = 1.. n. (формула Байеса). = Р(Х=х
= Р(Х=х 


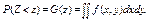 где f(x,y) – совместная плотность системы случайных величин (X, Y), а двойной интеграл берется по области D(Z) плоскости хОу, для которой j(x,y) < z.
где f(x,y) – совместная плотность системы случайных величин (X, Y), а двойной интеграл берется по области D(Z) плоскости хОу, для которой j(x,y) < z.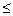 F(x)
F(x) 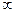 ) = lim F(x)=0.
) = lim F(x)=0.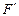 (x)=f(x) или F(x) =
(x)=f(x) или F(x) = 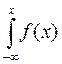
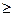 0
0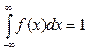
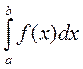 .
.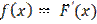
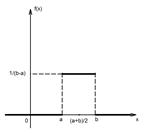 Непрерывная случайная величина Х имеет равномерный закон распределения на отрезке [a,b], если ее плотность вероятности постоянна на этом отрезке и равна 0 вне его:
Непрерывная случайная величина Х имеет равномерный закон распределения на отрезке [a,b], если ее плотность вероятности постоянна на этом отрезке и равна 0 вне его: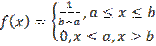 Кривая распределения равномерного закона R(a,b)
Кривая распределения равномерного закона R(a,b)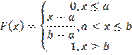
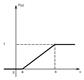
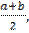 D[x] =
D[x] = 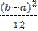 , Ass = 0, Ex = -1.2
, Ass = 0, Ex = -1.2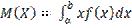
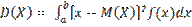 Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу [а, b], равна определенному интегралу от плотности распределения, взятому в пределах от а до b: P(a < X < b) =
Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу [а, b], равна определенному интегралу от плотности распределения, взятому в пределах от а до b: P(a < X < b) = 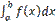
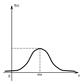 Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью:
Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью: 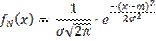
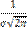 Нормальное распределение определяется двумя параметрами: m и σ.
Нормальное распределение определяется двумя параметрами: m и σ.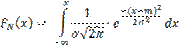
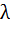
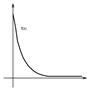 Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины Х,с параметром
Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины Х,с параметром 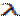 , которое описывается плотностью
, которое описывается плотностью 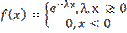
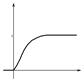 M(x) =
M(x) = 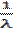 , Dx =
, Dx = 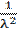
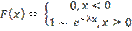
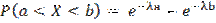
 Для нормального закона:
Для нормального закона:  .
. .
.

 и с учетом поправки на группировку Шеппарда:
и с учетом поправки на группировку Шеппарда: 


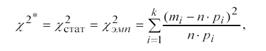
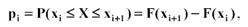
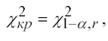
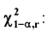 при
при 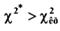 гипотеза отвергается (противоречит опытным данным),
гипотеза отвергается (противоречит опытным данным),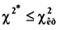 - гипотеза принимается (не противоречит опытным данным).
- гипотеза принимается (не противоречит опытным данным).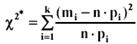 - имеет распределение “хи”-квадрат только при, n→∞следовательно, необходимо, чтобы в каждой интервальной группировке было достаточное число наблюдений (≥ 5), в противном случае соседние интервалы объединяют или заново стоят группировку.
- имеет распределение “хи”-квадрат только при, n→∞следовательно, необходимо, чтобы в каждой интервальной группировке было достаточное число наблюдений (≥ 5), в противном случае соседние интервалы объединяют или заново стоят группировку.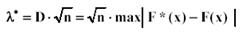
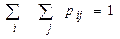 .
.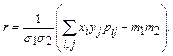
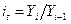 . Если же для сравнения взят общий уровень, то такие показатели называются базисными, т.е. базисные коэффициенты (темпы) роста равны
. Если же для сравнения взят общий уровень, то такие показатели называются базисными, т.е. базисные коэффициенты (темпы) роста равны 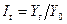 . Здесь
. Здесь 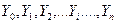 - последовательность абсолютных уровней ряда.
- последовательность абсолютных уровней ряда.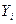 и уровнем, который предшествует ему, т.е.
и уровнем, который предшествует ему, т.е. 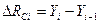 . Базисный абсолютный прирост исчисляется как разность между сравниваемым уровнем
. Базисный абсолютный прирост исчисляется как разность между сравниваемым уровнем 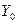 , т.е.
, т.е. 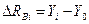 .
.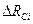 к предшествующему уровню
к предшествующему уровню 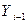 , т.е.
, т.е. 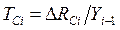 . Базисный темп прироста - отношение сравниваемого базисного абсолютного прироста
. Базисный темп прироста - отношение сравниваемого базисного абсолютного прироста 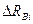 к уровню, принятому за постоянную базу
к уровню, принятому за постоянную базу 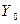 , т.е.
, т.е. 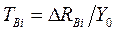 .
.