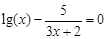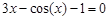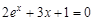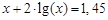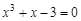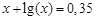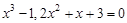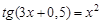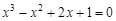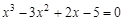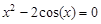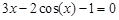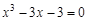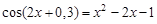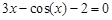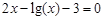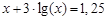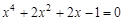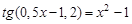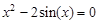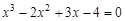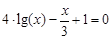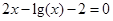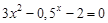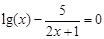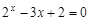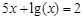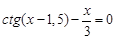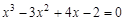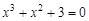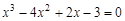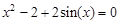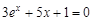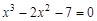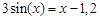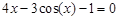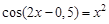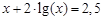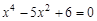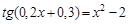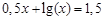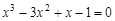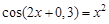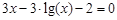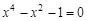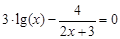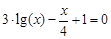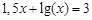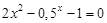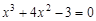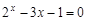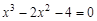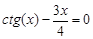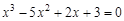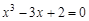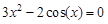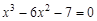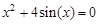Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Lab 3. Approximate solution of nonlinear equations. The method of chords, tangents (Newton).
I) Find approximate solutions of equation We separate the roots of this equation graphically (you can program). To do this, we construct graphs of functions
Consider as an example the first root. Clarify its method of chords. For this function to determine the sign
Because the where the fixed point
Where
The scheme of the chord method. We estimate the approximation error. As А) Then, using the estimate of the error
we get Therefore, the approximate value of the root is equal to We write the approximate value of the root only true significant digits in the narrow sense. We have Let us find the number of correct digits for Ответ: Б) Верна так же следующая формула оценки погрешности приближенного значения корня:
Для нашего уравнения имеем Тогда полагая
Следовательно, приближенное значение корня равно Запишем приближенное значение корня только верными значащими цифрами в узком смысле. Имеем Найдем число верных знаков для Так как Ответ: II) Найти приближенные решения уравнения Отделим корни этого уравнения графически (можно и программно). Для этого построим графики функций В качестве примера рассмотрим второй корень. Уточним его методом касательных. Для этого определим знаки функции Поскольку
Схема применения метода касательных.
Оценим погрешность приближения. Так как А) Тогда используя оценку погрешности
получим Следовательно, приближенное значение корня равно
Запишем приближенное значение корня только верными значащими цифрами в узком смысле. Имеем Найдем число верных знаков для Имеем Ответ: Б) Верна так же следующая формула оценки погрешности приближенного значения корня:
Для нашего уравнения имеем
Следовательно, приближенное значение корня равно Запишем приближенное значение корня только верными значащими цифрами в узком смысле. Имеем Округлим Найдем число верных знаков для Ответ: Вопросы самоконтроля. 1) Какой должна быть приближенное решение нелинейных уравнений? 2) Какие условия Метод хорд, касательных (Ньютона). 3) Какой должна быть величина шага при отделении корней? 4) Найти приближенные решения уравнения Лабораторная работа № 4 Тема: Решение нелинейных уравнений. Метод итерации. Задание: 1) Отделить корни уравнения графически и программно. 2) Уточнить один из корней уравнения методом итерации с точностью 3) Нарисовать схему применения метода итерации к данному корню уравнения. Вопросы самоконтроля. 1) Как отделяются корни уравнения? 2) Какой должна быть величина шага при отделении корней? 3) Какие условия должны быть выполнены для применения метода итерации? 4) Какова идея метода итерации? Геометрическая иллюстрация. 5) Какое условие должно выполняться для сходимости итерационной последовательности? 6) Как находится равносильное уравнение, применяемое для итерационного процесса? Критерий выбора равносильного уравнения.
7) Как определяется погрешность метода итерации при заданной точности? 8) Какие положительные и отрицательные стороны метода итерации (сравнить с методом деления отрезка пополам)?
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 301; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.200.211 (0.029 с.) |
 Lab 3. Approximate solution of nonlinear equations. by chords with precision
Lab 3. Approximate solution of nonlinear equations. by chords with precision  .
. ,
, 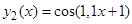 and find the abscissa plots the points of intersection of these functions:
and find the abscissa plots the points of intersection of these functions: 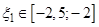 ,
, 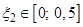 .
.
 and its second derivative
and its second derivative  on this section
on this section  .
. ,
, ;
; ,
, 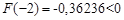 ; as
; as  , то
, то  ,
,  .
. , then apply the formula
, then apply the formula 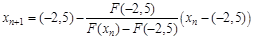 ,
, , as the starting point
, as the starting point  . We obtain the following table
. We obtain the following table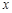
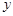


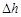

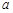
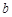

 ,
,  ,
,  .
.
 does not change its sign on this interval, the
does not change its sign on this interval, the  It reaches its maximum and minimum values at the endpoints
It reaches its maximum and minimum values at the endpoints  , so
, so 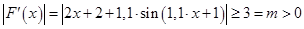 for
for 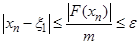 ,
, 
 ,
,  .
. .
.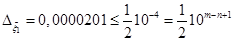 ,
, 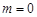 ,
,  . Rounded
. Rounded 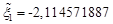 до
до  . We get
. We get  ,
,  ,
,  .
.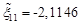 . We have
. We have  ,
,  ,
, 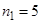 . Так как
. Так как 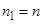 , то получим приближенное значение корня с числом верных знаков
, то получим приближенное значение корня с числом верных знаков  .
. ,
,  .
.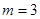 ,
,  .
. .
. .
. ,
,  . Округлим
. Округлим  ,
, 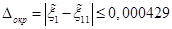 ,
,  .
. ,
, 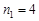 .
. , то получим приближенное значение корня
, то получим приближенное значение корня  .
. методом касательных (методом Ньютона) с точностью
методом касательных (методом Ньютона) с точностью  .
. ,
, 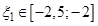 ,
,  .
. и второй ее производной
и второй ее производной 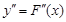 на этом отрезке
на этом отрезке  :
: 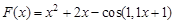 ,
,  ;
;  ,
, 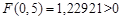 ; так как
; так как  , то
, то  ,
,  .
. , то применяем формулу
, то применяем формулу  ,
, 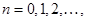
 .
.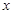


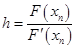

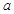


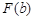


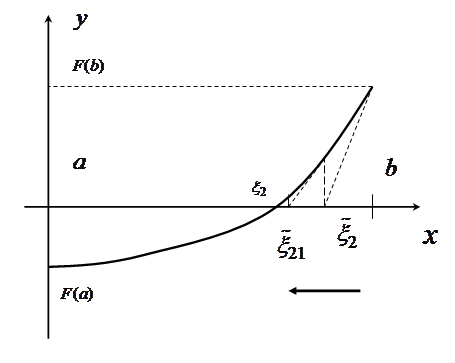
 не меняет свой знак на данном отрезке, то
не меняет свой знак на данном отрезке, то 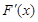 достигает своего наибольшего и наименьшего значения на концах отрезка
достигает своего наибольшего и наименьшего значения на концах отрезка 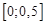 , поэтому
, поэтому  для
для 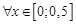 .
.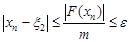 ,
, 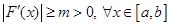
 ,
, 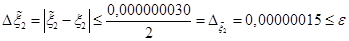 .
. .
. ,
,  ,
,  . Округлим
. Округлим 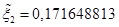 до
до  , с погрешностью округления
, с погрешностью округления  ,
,  .
. ,
, 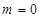 ,
,  . Так как
. Так как  , то получим приближенное значение корня с числом верных знаков
, то получим приближенное значение корня с числом верных знаков  .
. ,
,  .
. ,
, 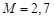 . Тогда полагая
. Тогда полагая 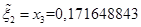 , получим
, получим .
. .
. ,
,  .
. до
до 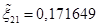 ,
,  ,
, 
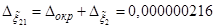
 ,
,  . Так как
. Так как 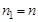 , то получим приближенное значение корня с числом верных знаков
, то получим приближенное значение корня с числом верных знаков  .
.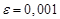 , указать число итераций.
, указать число итераций.