Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Lab 1. Fundamentals of the theory of errorsСтр 1 из 8Следующая ⇒
Lab 1. Fundamentals of the theory of errors Objective: Learn some basic concepts of the theory of errors. Task 1: Dan number partial sums of
Algorithm and implementation of solutions TO MS EXCEL Algorithm Find the sum of a number of analytically. Using the function. For each N calculate the absolute error. Let а – exact value, а * – the exact value of the approximate value of a certain value. Absolute error of the approximate value а * It is the quantity Determine the number of correct digits in
The number of significant digits and * called all the numbers in its records, starting with the first non-zero left. Significant digits of a * is called valid if the absolute error does not exceed the number of discharge units corresponding to this figure. Approximate number can be represented as a finite decimal fraction Then, if the figure in the image of a * true, then the inequality
Dan number
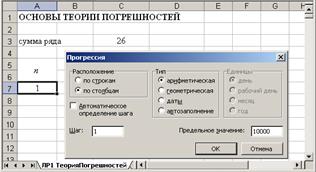
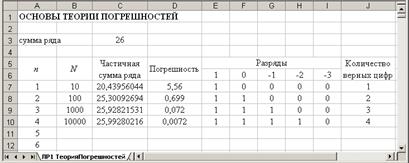
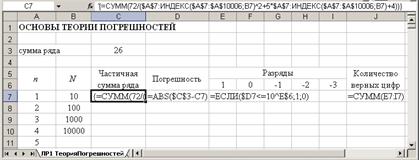
Implementation in MS Excel 3.1 To calculate the sum of the series to create the n auxiliary column: Edit - Fill - Progression...: 3.1 Carry out the calculation: View the worksheet with the result of the calculation Worksheet with formulas
Notes: The curly brackets indicate that the corresponding formula is derived array, ie, using a combination of Ctrl + Shift + Enter... Control questions:
1. What is called absolute and relative accuracy of the approximate number? 2. What is called the significant digit number? 3. What is called the true number of characters? 4. Formulate valuation rules limiting errors when performing operations on the approximate numbers.
Lab number 2 Subject: Solution of nonlinear equations. bisection method. Task: 1) Separate the roots of the equation graphically and analytically. 2) Clarify the roots (all!) Of the bisection method with a precision Questions of self-control 1) How to separate the roots of the equation? 2) What should be the value of the step at the roots of the department? 3) What conditions must be met for the application of the method of bisection of the segment?
A sample implementation of laboratory work number 2 (The solution of nonlinear equations. Bisection method.) Formulation of the problem. Find the root of the nonlinear equation The solution of the problem. Separate the root of the equation on the interval
We have
We select the segment
Approximate solution Therefore, the approximate value of the root is equal to We write the approximate value of the root only true significant digits in the narrow sense. We have Let us find the number of correct digits for Answer: Subject: Solution of nonlinear equations. method of chords and tangents method Task: 1) Separate the roots of the equation graphically and programmatically. 2) Clarify the roots of this method with the accuracy 3) Draw a diagram of the method to each root of the equation.
Questions of self-control
1) What is the idea of the method of bisection of the segment? Geometric illustration. 2) How do you calculate the approximate root of the equation and what is its uncertainty? 3) As a result of the error depends on the choice of the approximate solution? Лабораторная работа № 4 Тема: Решение нелинейных уравнений. Метод итерации. Задание: 1) Отделить корни уравнения графически и программно. 2) Уточнить один из корней уравнения методом итерации с точностью 3) Нарисовать схему применения метода итерации к данному корню уравнения. Вопросы самоконтроля. 1) Как отделяются корни уравнения? 2) Какой должна быть величина шага при отделении корней? 3) Какие условия должны быть выполнены для применения метода итерации? 4) Какова идея метода итерации? Геометрическая иллюстрация. 5) Какое условие должно выполняться для сходимости итерационной последовательности? 6) Как находится равносильное уравнение, применяемое для итерационного процесса? Критерий выбора равносильного уравнения. 7) Как определяется погрешность метода итерации при заданной точности? 8) Какие положительные и отрицательные стороны метода итерации (сравнить с методом деления отрезка пополам)?
Теоретические сведения Дана система n линейных уравнений с n неизвестными
Если система имеет единственное решение, то значения Наиболее распространенным является метод Гаусса, согласно которому путем последовательного исключения неизвестных система (1) приводится к треугольному виду:
Приведение матрицы системы к виду (2) называется прямым ходом. Вычисление неизвестных – обратным ходом. Необходимость округлять в промежуточных вычислениях приводит к тому, что возникает очень большая погрешность округления, искажающая результат. Существует несколько видов вычислительных схем метода Гаусса, в различной степени уменьшающих погрешность округления. Наиболее эффективной является “схема с выбором главного элемента”.
Прямой ход Исключение неизвестных в прямом ходе осуществляется по этапам. На каждом i-м этапе (i=1, 2, …, n) среди коэффициентов при неизвестном выбираем наибольший по абсолютной величине – “главный элемент”. Строка, его содержащая, называется главной. Затем главную строку прибавляем ко всем остальным строкам, предварительно умножив ее на специально подобранные числа
Главная строка i-го этапа в дальнейших преобразованиях не участвует, поэтому для приведения системы (1) к виду (2) нужно проделать
Обратный ход Вначале из уравнения в последней строке находится
Прямой ход В первом столбце поставим номера разделов. Раздел первый
2. В графы, отведенные для матриц, записываем коэффициенты при неизвестных и свободные члены, приписывая в качестве двух запасных значащих цифр нули. 3. В каждой строке вычисляем алгебраическую сумму коэффициентов и свободного члена и записываем в столбец контрольных сумм. Так, например, для первой строки
4. Среди элементов первого столбца выбираем наибольший по абсолютной величине, подчеркиваем строку, в которой он стоит и выписываем ее в качестве первой строки в таблицу для обратного хода. Здесь главной будет первая строка, главный элемент равен 2,000. 5. Элементы всех строк первого столбца, кроме главного, делим на него и результат с противоположным знаком записываем в столбец
Раздел второй 6. Исключаем элементы первого столбца, кроме главного. Для этого главную строку, умноженную на
7. Контроль: складываем полученные коэффициенты при неизвестных и свободный член 8. Аналогично вычисляем вторую и третью строки второго раздела
9. Проводим контроль, как в п. 7.
10. Среди коэффициентов при неизвестном Далее, делим на главный элемент все числа, стоящие с ним в одном столбце (0,300 и -0,300), результаты записываем с противоположным знаком в качестве
11. Третий раздел будет иметь две строки. Главный элемент выбираем среди коэффициентов при
Обратный ход 1. Последняя строка таблицы соответствует уравнению 2. Контроль: вместо свободного члена
3. Найденное значение
Контроль:
4. Найденные значения
5. Из первого уравнения получим Проверка. Значения неизвестных
Значения невязок малы, т.е. нулей до первой значащей цифры больше, чем было знаков после запятой в исходных данных, значит, вычисления проведены верно. Невязки запишем на свободное место в столбец первого раздела. Ответ: Решением данной системы будет вектор
1. Матричные функции Excel Для решения задач линейной алгебры используются матричные функции Excel из категории математические: МУМНОЖ(<матрица1>;<матрица2>) – возвращает произведение матриц. МОБР(<матрица>) – возвращает матрицу, обратную к данной. МОПРЕД(<матрица>) – вычисляет определитель исходной квадратной матрицы. Порядок обращения к матричным функциям: Ø выделить блок, где будет размещен результат матричной операции; Ø Ø убрать окно соответствующей функции (с помощью кнопки) или отбуксировать его в сторону от исходных данных; Ø выделить исходную матрицу (бегущая пунктирная линия); Ø одновременно нажать клавиши Shift+Ctrl+Enter. 1. Реализация метода Гаусса средствами приложения Excel Пример 1.1. Найти решение системы линейных алгебраических уравнений
используя алгоритм метода Гаусса.
Последовательность действий: Возьмем чистый лист Excel, назовем его Гаусс. Введем расширенную матрицу системы, как показано на рис.1.1 в ячейки А3:D5. Первый этап, приведение матрицы системы к треугольной. 1. Поделим элементы первой строки на а11 .Для этого в ячейку А7 введем формулу А7=А3/A$3$ (*смотри сноску) и скопируем ее вправо до конца строки. 2. Умножим элементы первой строки на (-а21) и прибавим ко 2-ой строке. Для этого введем формулу А8=А7(-А$4$)+А4 и скопируем ее вправо до конца строки. 3. Умножим элементы первой строки на (- а31 ) и прибавим к 3-ей строке. Для этого введем формулу А9=А7(-А$5$)+А5 и скопируем ее вправо до конца строки. Таким образом исключили неизвестное х1 из 2-го и 3-го уравнений системы (смотри 1-ый шаг рис.1.1). 4. Осталось исключить неизвестное х2 из 3-го уравнения системы. Для этого реализуем описанный выше алгоритм для 2-ой и3-ей строк (смотри 2-ой шаг рис.1.1).
Рис.1.1. На этом первый этап метода Гаусса, закончен, матрица системы приведена к треугольной. Второй этап. Здесь последовательно найдем неизвестные, начиная с последней строки. Для этого в ячейки G12:G14 запишем формулы:
G4=D13/C13 (для вычисления x 3); G3=D12-C12*G4 (для вычисления x2); G2=D11-C11*G4-B11*G3 (для вычисления x1).
Последовательность действий 1.
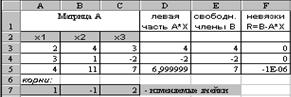
Возьмем новый лист (а можно и на том же). Заготовим таблицу, как показано на рис.1.2. Рис.1.2. 2. Заготовим ячейки А7:С7, где будет сформировано решение системы (х1, х2, х3). Первоначально они остаются пустыми, т.е. равными нулю. Однако для контроля правильности вводимых далее формул, удобно ввести в эти ячейки какие-либо значения, например единицы. Эти значения можно рассматривать как нулевое приближение решения системы, 3. Введем коэффициенты системы (матрицу А) в ячейки А3:С5. 4. В столбец D введем выражения для вычисления левых частей исходной системы. Для этого в ячейке D 3 введем и скопируем вниз до конца таблицы формулу: D3=СУММПРОИЗВ (A3:C3;$A$7:$C$7). Используемая функция СУММПРОИЗВ принадлежит категории Математические. 5. В столбец Е запишем значения правых частей системы матрицу 6. 7. Будет не лишним проверить правильность вычислений для случая 8. Зададим команду меню Сервис\Поиск решения. В окне Поиск решения (рис.1.3) в поле Изменяя ячейки укажем блок $А$7:$С$7, а в поле Ограничения – $F$3:$F$5 =0. Для этого надо щелкнуть на кнопке Добавить и ввести эти ограничения. 9. Щелкнем на кнопке Выполнить. Рис. 1.3. Полученное решение системы (1.8) х1 =1; х2 =-1 х3 =2 записано в ячейках А7:С7, рис.1.2.
Вопросы самоконтроля. 1) Как отделяются корни уравнения? 2) Как используется функция СУММПРОИЗВ? 3) Какой должна быть величина шага при отделении корней? 4) Какие условия должны быть выполнены для применения метода половинного деления отрезка?
Задания к лабораторным работам № 5-7
Найти решение данной системы
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 279; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.54.199 (0.221 с.) |
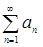 . Find the sum of a number of analytically. Calculate
. Find the sum of a number of analytically. Calculate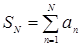 and find the value of errors in values N = 10, 102, 103, 104.
and find the value of errors in values N = 10, 102, 103, 104.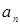
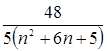
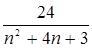
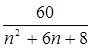
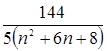
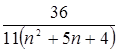
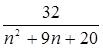
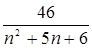
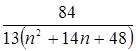
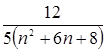
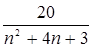
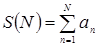 , calculate the partial sums of the indicated values N.
, calculate the partial sums of the indicated values N.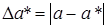 .
.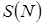 .
.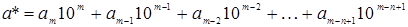
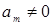 .
.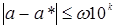 ,
, 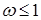 , more often
, more often 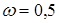 .
.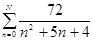
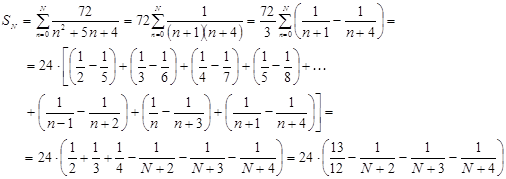
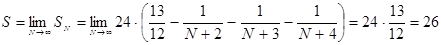 .
.
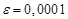 specify the number of partitions of the interval.
specify the number of partitions of the interval.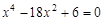
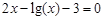
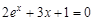
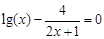
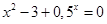
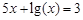
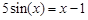
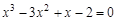
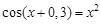
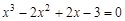
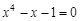
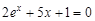
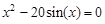
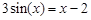
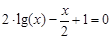
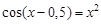
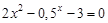
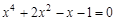
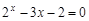

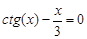
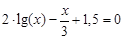
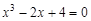
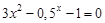
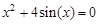
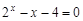
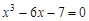
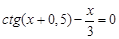
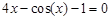
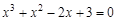
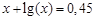
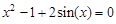
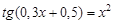
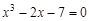
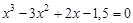
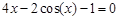
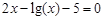
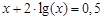
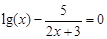
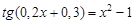
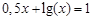
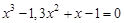
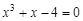
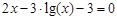
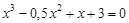
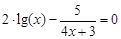
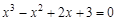
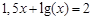
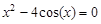
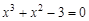
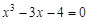
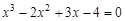
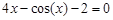
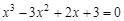
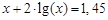
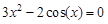
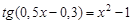
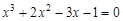
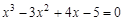
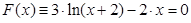 bisection method with a precision
bisection method with a precision 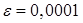 .
.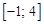 graphical method. For this function tabeliruem
graphical method. For this function tabeliruem 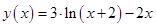 in this segment
in this segment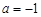 ,
, 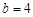 ,
, 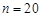 ,
, 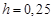
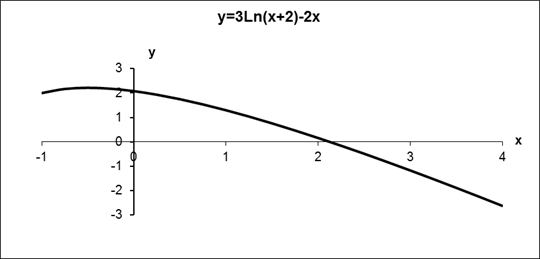
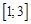 , containing isolated root, to clarify that the bisection method applicable under the scheme
, containing isolated root, to clarify that the bisection method applicable under the scheme 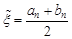 ,
, 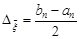 ,
, 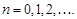 ,
, 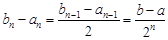 ,
, 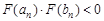 . believing
. believing 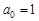 ,
, 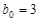 , as well as the condition to stop the interval bisection
, as well as the condition to stop the interval bisection 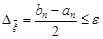 , up a table
, up a table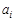
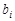
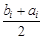
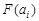
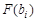
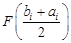
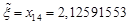 , error
, error 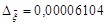 , number of iterations
, number of iterations 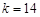 .
.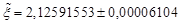 .
.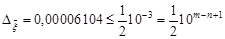 ,
, 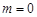 ,
, 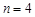 . Rounded
. Rounded 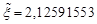 до
до 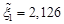 ,
, 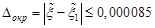 ,
, 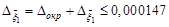 .
.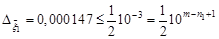 ,
, 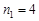 . As
. As 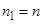 , we obtain an approximate value of the root of the number of correct digits
, we obtain an approximate value of the root of the number of correct digits 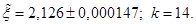
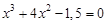
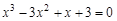
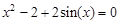
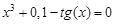
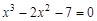
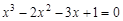
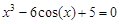
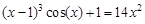
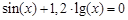
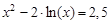
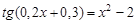
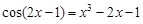
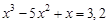
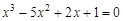
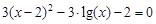
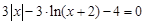
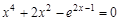
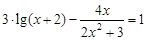
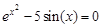
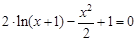
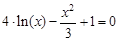
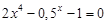
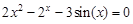
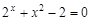
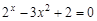
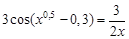
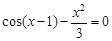
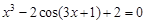
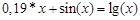
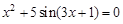

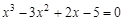
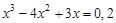
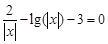
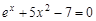
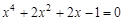
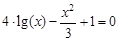
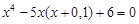
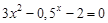
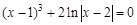
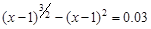
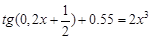
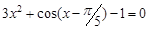
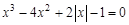
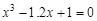
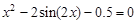
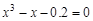
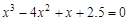
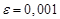 , указать число итераций.
, указать число итераций.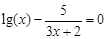
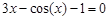
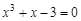
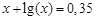
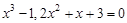
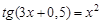
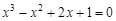
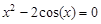
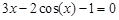
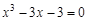
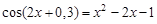
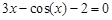
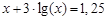
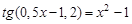
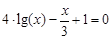
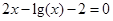
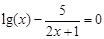
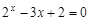
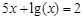
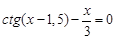
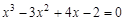
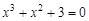
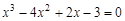
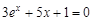
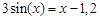
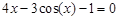
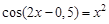
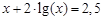
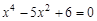
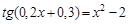
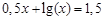
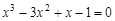
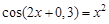
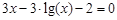
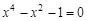
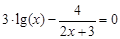
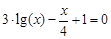
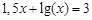
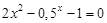
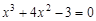
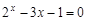
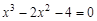
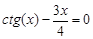
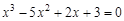

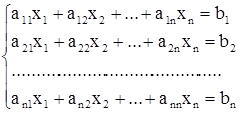 (1)
(1)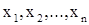 могут быть найдены по известным формулам Крамера, но этот способ неудобен и приходится применять приближенные или численные методы решения.
могут быть найдены по известным формулам Крамера, но этот способ неудобен и приходится применять приближенные или численные методы решения.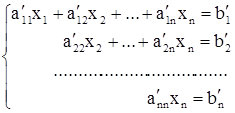 (2)
(2)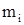 так, чтобы коэффициенты при
так, чтобы коэффициенты при 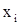 во всех строках, кроме главной, обратились бы в нуль.
во всех строках, кроме главной, обратились бы в нуль.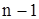 исключение неизвестных.
исключение неизвестных.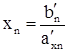 , затем это значение подставляется в предыдущее главное уравнение, которое разрешается относительно
, затем это значение подставляется в предыдущее главное уравнение, которое разрешается относительно 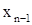 , и т.д.
, и т.д.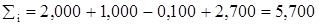 .
.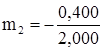 ,
, 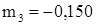 ,
, 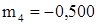 .
.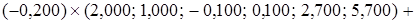
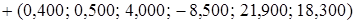 =
=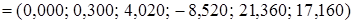 .
.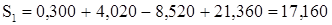 . Строчная сумма
. Строчная сумма 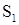 совпадает с контрольной
совпадает с контрольной 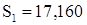 , значит, эта строка найдена без ошибки.
, значит, эта строка найдена без ошибки.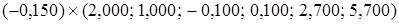 +
+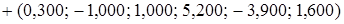 =
=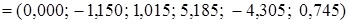 .
.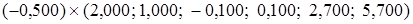 +
+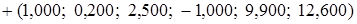 =
=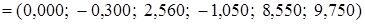 .
.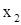 выбираем главный (-1,150), подчеркиваем главную строку и записываем ее в качестве второй в таблицу для обратного хода.
выбираем главный (-1,150), подчеркиваем главную строку и записываем ее в качестве второй в таблицу для обратного хода.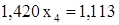 . Отсюда находим
. Отсюда находим 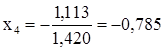 .
.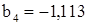 берем
берем 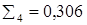 , находим
, находим 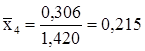 . Проверяем выполнение условия
. Проверяем выполнение условия 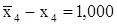 :
: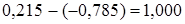 .
.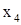 подставляем в следующее уравнение, соответствующее третьей главной строке:
подставляем в следующее уравнение, соответствующее третьей главной строке: 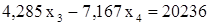 , отсюда
, отсюда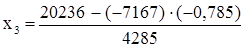 .
.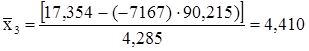 ,
,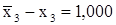 .
.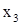 и
и 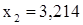 . Также по известным
. Также по известным 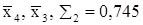 получим
получим 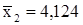 .
.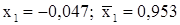 .
.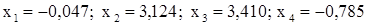 подставим в каждое из уравнений исходной системы и подсчитаем невязки (см. разд. 3):
подставим в каждое из уравнений исходной системы и подсчитаем невязки (см. разд. 3):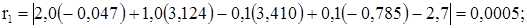
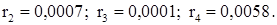
 (в ответе оставляем только 1 запасную цифру).
(в ответе оставляем только 1 запасную цифру). в мастере функций выбрать нужную категорию и нужную функцию;
в мастере функций выбрать нужную категорию и нужную функцию;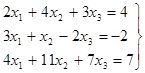 , (1.8)
, (1.8)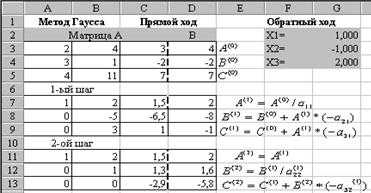
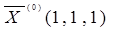 .
.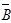 .
.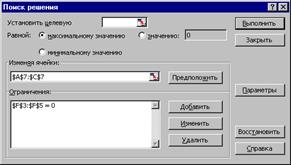 В столбец F введем невязки в соответствии с формулой (1.9), т.е. введем формулу F3=D3-E3 и скопируем ее вниз до конца таблицы.
В столбец F введем невязки в соответствии с формулой (1.9), т.е. введем формулу F3=D3-E3 и скопируем ее вниз до конца таблицы.