
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Властивості інтеграла Лебега від простих функцій
1. Проста функція
Доведення. Нехай
Отже, функція
2. Якщо проста функція
Доведення. Обмеженість простої функції
Зауваження 5.1.2. Ця властивість теж підкреслює перевагу інтеграла Лебега в порівнянні з інтегралом Рімана, тому, що, як відомо є обмежені функції (наприклад, функція Діріхле) які не інтегровні за Ріманом.
3. Нехай
і якщо суми в (5.1.1) скінченні, то
тобто існування інтеграла і сам інтеграл не залежить від того, як зображена проста функція. Доведення. Кожну множину
Суму зліва, використовуючи s-адитивність міри, можливо зобразити у вигляді:
Аналогічно, суму справа в (5.1.3) зобразимо у вигляді:
З (5.1.3) і одержаних рівностей випливає (5.1.1). Якщо суми в (5.1.1) скінченні, то з аналогічних міркувань випливає рівність (5.1.2) і
4. Якщо проста функція Доведення. Нехай
Отже 5. Якщо проста функція
Доведення. Нехай
Отже функція l
6. Якщо прості функції
Доведення. Нехай
Отже функція
Зауваження 5.1.3. Поняття простої на множині A функції пов’язано з розбиттям множини A на не більш ніж зчисленну суму вимірних множин. З доведення попередньої властивості випливає, що якщо
7. Якщо для простих інтегровних за Лебегом на множині
Доведення. Нехай
Ця властивість називається монотонністю інтеграла.
8. Якщо для простих на множині
Доведення. Нехай
Отже функція
Наслідок 5.1.1. Нехай Дійсно, якщо Зауваження 5.1.4. Відомо, що якщо функція
9. Якщо для простих на множині Доведення. З умови випливає нерівність
і отже нерівність
Використовуючи останню нерівність, наслідок 5.1, приклад 1, властивості 6 і 8 інтеграла одержимо властивість 9.
10. Адитивність інтеграла Лебега. Нехай простафункція
і, якщо справа маємо ряд, то він збігається абсолютно. Доведення. Нехай
Так як простафункція Рівність (5.1.4) випливає з (5.1.5), якщо в (5.1.5) усюди убрати знак модуля.
11. Нехай
то функція Доведення. Нехай
і, оскільки
Отже, функція Теорема 5.1.1. (Критерій вимірності функції в термінах простих функцій). Для того щоб скінченна на множені Доведення. Достатність випливає з теореми 4.1.2 про граничний перехід у класі вимірних функцій. Доведемо необхідність. Для будь-якого натурального розглянемо множини
Оскільки функція
Отже, послідовність простих функцій Теорема доведена.
|
||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 311; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.249.105 (0.037 с.) |
 , що задана на множині
, що задана на множині  міри нуль, інтегровна за Лебегом і
міри нуль, інтегровна за Лебегом і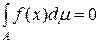 .
. , якщо
, якщо  , де множини
, де множини  попарно неперетинні, вимірні, їх не більш ніж зчисленна кількість і
попарно неперетинні, вимірні, їх не більш ніж зчисленна кількість і  . Так як
. Так як  , то для будь-якого
, то для будь-якого  :
: 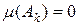 і тоді
і тоді .
.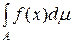 =
=  .
. , то вона інтегровна за Лебегом і
, то вона інтегровна за Лебегом і .
. , де
, де  значення функції
значення функції 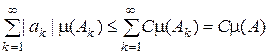 . Отже функція
. Отже функція 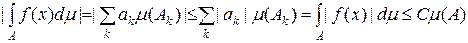 .
.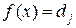 , якщо
, якщо  , де множини
, де множини 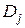 попарно неперетинні, вимірні, їх не більш ніж зчисленна кількість,
попарно неперетинні, вимірні, їх не більш ніж зчисленна кількість,  . Тоді
. Тоді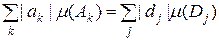 (5.1.1)
(5.1.1)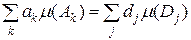 , (5.1.2)
, (5.1.2)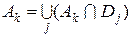 ,
,  . Окрім того,
. Окрім того,  , якщо
, якщо  . Отже
. Отже . (5.1.3)
. (5.1.3) .
.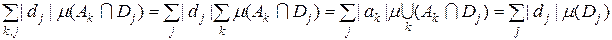 .
.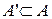 .
.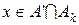 і
і 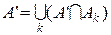 . Так як
. Так як  , то
, то .
.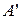 .
.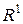 інтегровна за Лебегом функція l
інтегровна за Лебегом функція l  .
. , якщо
, якщо  .
.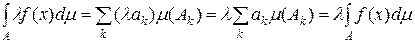 .
. інтегровні за Лебегом на множині
інтегровні за Лебегом на множині  .
. , якщо
, якщо  , якщо
, якщо 


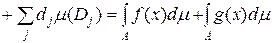 .
. .
. , якщо
, якщо  , і тоді
, і тоді .
. £
£ 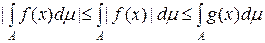 .
. , і
, і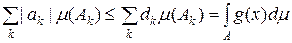 .
.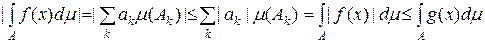 .
. .
.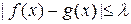 , де
, де  деяке дійсне число, і функція
деяке дійсне число, і функція 
 .
. деяке розбиття множини
деяке розбиття множини 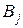 . Тоді
. Тоді (5.1.4)
(5.1.4) (5.1.5)
(5.1.5) .
.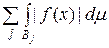 , (5.1.6)
, (5.1.6)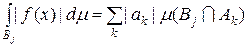
 , то використовуючи збіжність ряду (5.1.6) одержимо
, то використовуючи збіжність ряду (5.1.6) одержимо
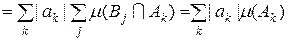 .
. , що рівномірно збігається на множені
, що рівномірно збігається на множені 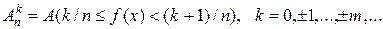
 вимірні і здійснюють розбиття множини
вимірні і здійснюють розбиття множини  , якщо
, якщо  . Функції
. Функції  . Нехай
. Нехай  , тоді знайдеться ціле число
, тоді знайдеться ціле число 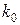 таке, що
таке, що 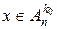 і
і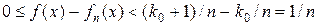 .
.


