
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття півкільця, кільця, s-алгебри
Означення 3.6.1. Система множин Á називається півкільцем, якщо вона містить порожню множину, перетин будь яких множин з Á, а також, якщо
Означення 3.6.2. Непорожня система множин Â називається кільцем, якщо вона разом з будь-якими множинами Будь-яке кільце є півкільцем. Дійсно, так як Â- не порожня множина, то існує Множина Приклади. 1. Нехай 2. Нехай 3. У прикладах 1,2 множина 4. Множина усіх відрізків 5. Множина усіх елементарних множин із 6. Множина усіх елементарних множин, що містяться у деякому сегменті 7. Множина усіх вимірних за Лебегом множин із 8. Множина усіх обмежених і вимірних за Лебегом множин із
Означення 3.6.3. Кільце Â називається s-кольцом, якщо Â разом з послідовністю Означення 3.6.4. Теорема 3.6.1. Доведення. Нехай Завдяки цієї теореми s-алгебру ще називають d-алгеброю. Зауваження 2. Внаслідок означення 3.5.4 і завдяки властивості 8 вимірних множин, множина усіх вимірних за Лебегом множин, що містяться у деякому інтервалі
Означення 3.6.5. Нехай Ã довільна система множин. Мінімальною (або найменшою) s-алгеброю, що містить систему множин Ã, називається перетин усіх s-алгебр, що містять систему множин Ã. Мінімальна s-алгебра існує. Нехай Означення 3.6.6. Мінімальна s-алгеброю, що містить систему усіх інтервалів, називається борельовою, а множини, що належать борельовою s-алгебри, називається борельовами множинами. Означення 3.6.7. Борельовами множинами відносно множини Зауваження 3. Із зауваження 1 і означення відносно борельових множин випливає, що s-алгебра борельових відносно деякому інтервала Зауваження 4. Так як s-алгебра усіх вимірних за Лебегом множин містить усі інтервали, то із означення s-алгебри борельових множин, як мінімальної s-алгебри, що містить усі інтервали, випливає, що кожна борельова множина вимірна за Лебегом. Більш того потужність множини усіх борельових множин є континуум, а потужність множини усіх вимірних за Лебегом множин більша за континуум. 3.7. Поняття вимірної множини в
Означення 3.7.1. Паралелепіпедом
Зокрема умови Очевидно, що перетин паралелепіпедів є паралелепіпед, умова Означення 3.7.2. Елементарними множинами в
Отже будь-яка елементарна множина Означення 3.7.3. Мірою будь якого паралелепіпеду Тобто незалежно від того, чи буде паралелепіпеду Означення 3.7.4. Мірою будь якої елементарної множини Властивості міри елементарних множин такі, як і в одномірному випадку. Тому і продовження міри за Лебегом здійснюється аналогічно. В загалі, якщо визначена міра на деякому півкільці Á, розглядається кільце Â усіх скінченних об’єднаннь
Узагальнення поняття вимірності в Нехай Можливі наступні три випадки. 1. Дискретна міра. В цьому випадку функція 2. Абсолютно неперервна міра. Вона визначається функцією 3. Сингулярна міра. В цьому випадку міра будь-якої скінченної множини дорівнює нулю, проте існує множина Приведемо приклад такої міри. Розглянемо інтервали 1. 2. Функція 3. Функція Покажемо, що функція
Функція Зауважимо, що в загальному випадку міра може визначатися як сума розглянутих мір. Загальне поняття міри Нехай Â(X) - деяка s-алгебра підмножин множини X. Дійсна функція m множини називається мірою, якщо вона визначена на Â(X), приймає невід’ємні значення і s-адитивна, тобто 1. 2. 3. Пара (X, Â(X)) називається вимірним простором, а трійка (X, Â(X),m), де міра m визначена на s-алгебрі Â(X), називається простором з мірою. Зокрема, якщо міра m нормована умовою ГЛАВА IY ВИМІРНІ ЗА ЛЕБЕГОМ ФУНКЦІЇ
Означення вимірної функції. Означення 4.1.1 Функцією Це відоме означення функції. Доповнимо його – будемо надалі вважати, що функція може приймати і нескінченні значення При цьому правила дії над цими «невласними» числами і звичайними числами визначаються так, щоб операція суми і добутку були комутативні і асоціативні. При цьому сума і різниця нескінченнності і звичайного числа дорівнює нескінченності того же знаку, добуток нескінченності на число, що не дорівнює нулю, а також добуток нескінченності на нескінченність, дорівнює нескінченності, знак якої визначається як і до добутку чисел, добуток нескінченності на нуль є нуль. Частка довільного числа і нескінченності є нуль. Сума нескінченностей одного знаку дорівнює нескінченності того же знаку. Різниця нескінченностей різних знаків є нескінченність зі знаком зменшуваного. Не мають сенсу сума нескінченностей різних знаків, різниця нескінченностей одного знаку, частка нескінченностей. Надалі вважаємо, що функція
Введемо позначення:
Означення 4.1.2. Функція Теорема 4.1.1 (Критерій вимірності). Для того щоб функція Доведення. Нехай функція
Дійсно, якщо Вимірність множин
Нехай для будь-якого
Дійсно, якщо Нехай для будь-якого Теорема доведена.
Приклади вимірних функцій 1. Функція Дійсно 2. Функція Будь-яка проста функція 3. Функція Покажемо, що множина
|
||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 442; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.158.47 (0.047 с.) |

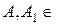 Á,
Á,  , то знайдуться попарно неперетинні множини
, то знайдуться попарно неперетинні множини 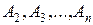 такі, що
такі, що . (3.6.1)
. (3.6.1)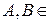 Â містить їх об’єднання, перетин і різницю.
 містить їх об’єднання, перетин і різницю.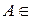 Â, отже
Â, отже 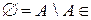 Â, і очевидно виконується умова (3.6.1): достатньо взяти
Â, і очевидно виконується умова (3.6.1): достатньо взяти 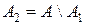 .
. системи множин називається одиницею системи Á, якщо до будь-якої множини
системи множин називається одиницею системи Á, якщо до будь-якої множини  з цієї системи
з цієї системи 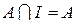
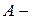 довільна множина, система множин
довільна множина, система множин 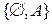 є кільце.
є кільце. є півкільце. Дійсно порожня множина
є півкільце. Дійсно порожня множина 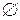 є інтервал
є інтервал 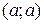 , перетин двох відрізків є відрізок і різниця двох відрізків є або відрізок або сума двох відрізків. Проте множина усіх відрізків не буде кільцем тому, що сума двох неперетинних відрізків не є відрізком.
, перетин двох відрізків є відрізок і різниця двох відрізків є або відрізок або сума двох відрізків. Проте множина усіх відрізків не буде кільцем тому, що сума двох неперетинних відрізків не є відрізком.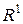 буде кільце. Це випливає з властивостей 1 – 4 елементарних множин. Одиниці немає, оскільки немає елементарної множини, що містить усі інші елементарні множини.
буде кільце. Це випливає з властивостей 1 – 4 елементарних множин. Одиниці немає, оскільки немає елементарної множини, що містить усі інші елементарні множини.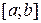 , є кільце. Сегмент
, є кільце. Сегмент 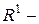 необмежена множина.
необмежена множина.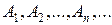 містить їх об’єднання
містить їх об’єднання 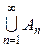 .
.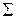 -кольцо Âз одиницею називається s-алгеброю.
-кольцо Âз одиницею називається s-алгеброю.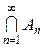 .
. одиниця s-алгебри Â і
одиниця s-алгебри Â і 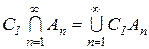 . Оскільки Â є s-алгеброю, то права частина належить Â, отже і
. Оскільки Â є s-алгеброю, то права частина належить Â, отже і 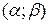 , буде s-алгеброю, одиниця якої є інтервал
, буде s-алгеброю, одиниця якої є інтервал 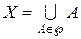 і Â(X) - s-алгебра усіх підмножин множини X. Перетин усіх s-алгебр, що містяться у Â(X) і містять систему множинÃ, і буде мінімальною s-алгеброю.
і Â(X) - s-алгебра усіх підмножин множини X. Перетин усіх s-алгебр, що містяться у Â(X) і містять систему множинÃ, і буде мінімальною s-алгеброю.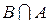 , де
, де 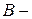 довільна множина.
довільна множина.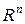
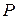 в просторі
в просторі 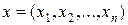 , координати яких задовольняють умови:
, координати яких задовольняють умови: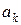 ¥
¥ 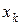 Ŧ
Ŧ 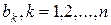 , де символи ¥, Ŧ незалежно один від одного приймають значення < або
, де символи ¥, Ŧ незалежно один від одного приймають значення < або 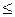 , і
, і 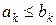 .
.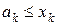
 , визначають звичайний паралелепіпед, а умови
, визначають звичайний паралелепіпед, а умови 
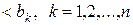 , - відкритий паралелепіпед.
, - відкритий паралелепіпед.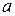
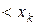
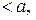
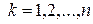 , визначає порожню множину, різницю двох паралелепіпедів можливо зобразити як об’єднання скінченної множини неперетинних паралелепіпедів, отже множина усіх паралелепіпедів є півкільце.
, визначає порожню множину, різницю двох паралелепіпедів можливо зобразити як об’єднання скінченної множини неперетинних паралелепіпедів, отже множина усіх паралелепіпедів є півкільце. має вигляд
має вигляд  , де
, де 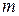 може бути довільним натуральним числом і паралелепіпеди
може бути довільним натуральним числом і паралелепіпеди 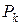 попарно не перетинаються.
попарно не перетинаються.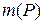 .
.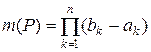 . Зокрема, міра паралелепіпеду меншої вимірності і міра порожньої множини дорівнює нулю.
. Зокрема, міра паралелепіпеду меншої вимірності і міра порожньої множини дорівнює нулю.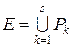 називається сума об’ємів паралелепіпедів
називається сума об’ємів паралелепіпедів  .
. , де
, де 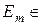 Á і продовжується міра спочатку на кільце Â, а потім і на більш широке кільце вимірних множин.
Á і продовжується міра спочатку на кільце Â, а потім і на більш широке кільце вимірних множин.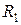
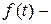 деяка неспадаюча неперервна зліва функція, що задана на сегменті
деяка неспадаюча неперервна зліва функція, що задана на сегменті 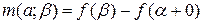 ,
, 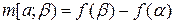 ,
, 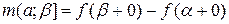 ,
, 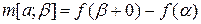 . Маючи міру на будь-якому відрізку, визначимо спочатку міру до будь-якої елементарної множини
. Маючи міру на будь-якому відрізку, визначимо спочатку міру до будь-якої елементарної множини 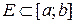 , а потім користуючись її адитивністю продовжимо за Лебегом на більш широку s-алгебру вимірних множин. Цю міру називають мірою Лебега-Стільтьєса і позначають символом
, а потім користуючись її адитивністю продовжимо за Лебегом на більш широку s-алгебру вимірних множин. Цю міру називають мірою Лебега-Стільтьєса і позначають символом 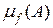 . У випадку, коли
. У випадку, коли  , вона збігається з мірою Лебега.
, вона збігається з мірою Лебега.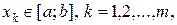 таких, що
таких, що 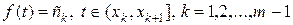 . Міра
. Міра  будь-якого відрізку
будь-якого відрізку 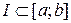 дорівнює
дорівнює 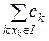 . Можливо розглянути функцію
. Можливо розглянути функцію 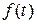 , що має зчисленну множину точок розриву.
, що має зчисленну множину точок розриву.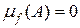 , якщо міра Лебега множини
, якщо міра Лебега множини 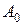 така, що міра Лебега множини
така, що міра Лебега множини  .
.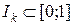 , що є складовими інтервалами канторової відкритої множини
, що є складовими інтервалами канторової відкритої множини 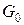 . Відомо, що
. Відомо, що  , де
, де 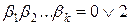 ,
, 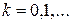 . Будь-яка точка
. Будь-яка точка 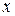 канторової замкнутої множини
канторової замкнутої множини 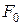 має вигляд
має вигляд 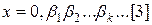 , де
, де 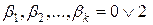 . Значок
. Значок 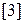 означає, що
означає, що 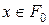 визначимо
визначимо 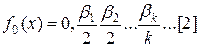 , де значок
, де значок 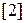 означає, що цій дріб подано у двійковий системи числення. У лівому кінці інтервалу
означає, що цій дріб подано у двійковий системи числення. У лівому кінці інтервалу 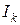 функція
функція 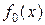 приймає значення:
приймає значення: 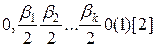 , а у правому теж саме значення:
, а у правому теж саме значення:  . Визначимо функцію
. Визначимо функцію 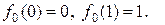
 . Дійсно, якщо
. Дійсно, якщо 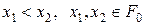 , то
, то 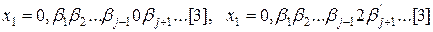 , де
, де 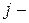 довільне натуральне число. Отже,
довільне натуральне число. Отже, 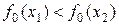 .
.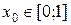 така, що
така, що 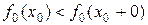 . Тоді, внаслідок того, що функція
. Тоді, внаслідок того, що функція 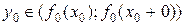 функція
функція 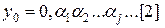 . Тоді функція
. Тоді функція 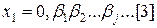 , де
, де 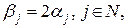 приймає значення
приймає значення 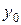 . Одержана суперечність спростовує припущення.
. Одержана суперечність спростовує припущення.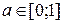 ,
, 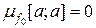 . Отже, завдяки адитивності міри
. Отже, завдяки адитивності міри  , міра будь-якої скінченної або зчисленної множини дорівнює нулю. Очевидно також, що
, міра будь-якої скінченної або зчисленної множини дорівнює нулю. Очевидно також, що 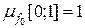 , а
, а 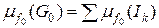 = 0 тому, що
= 0 тому, що 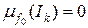 , бо функція
, бо функція 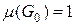 .
.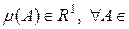 Â(X).
Â(X).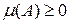 .
.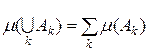 до будь-якої скінченної або зчисленної системи множин
до будь-якої скінченної або зчисленної системи множин 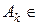 Â(X).
Â(X). , то трійка (X, Â(X),m)називається ймовірнісним простором, а елементи s-алгебри Â(X) - подіями.
, то трійка (X, Â(X),m)називається ймовірнісним простором, а елементи s-алгебри Â(X) - подіями.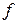 заданою на множені
заданою на множені  поставлено у відповідність число
поставлено у відповідність число  .
.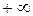 і
і  . Це можливо мотивувати наступним прикладом. Нехай частинні суми
. Це можливо мотивувати наступним прикладом. Нехай частинні суми 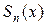 функціонального ряду
функціонального ряду 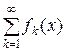 в точці
в точці 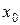 прямують до
прямують до 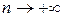 . Логічно визначити, що сума цього ряду в точці
. Логічно визначити, що сума цього ряду в точці 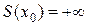 .
.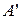 множини
множини 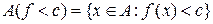 , де
, де 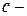 довільне дійсне число. Аналогічно визначаються множини
довільне дійсне число. Аналогічно визначаються множини 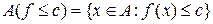 ,
,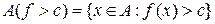 і
і 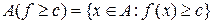 .
.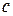 вимірна множина
вимірна множина 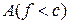 .
.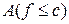 ,
,  ,
, 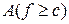 .
. .
.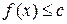 , то для будь-якого
, то для будь-якого 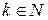 :
: 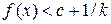 і слід елемент
і слід елемент  в
в 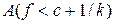 вимірні, то і множина
вимірні, то і множина  ,
, 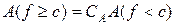 .
.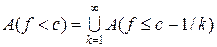 .
.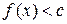 , то знайдеться натуральне число
, то знайдеться натуральне число  і слід елемент
і слід елемент 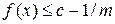 . А тоді
. А тоді  вимірні, то і множина
вимірні, то і множина 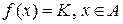 - вимірна.
- вимірна.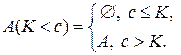
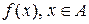 називається простою, якщо множину
називається простою, якщо множину  таких, що
таких, що 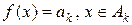 .
.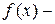 вимірна. Це випливає із вимірності функції
вимірна. Це випливає із вимірності функції 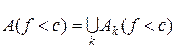 .
. , є вимірною. В даному прикладі
, є вимірною. В даному прикладі 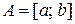 .
.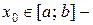 гранична точка множини
гранична точка множини 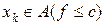 така, що
така, що 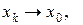 коли
коли 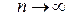 . Спрямувавши
. Спрямувавши  до нескінченності, з нерівності
до нескінченності, з нерівності 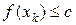 і неперервності функції
і неперервності функції 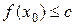 . Отже множина
. Отже множина 


