
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометричне застосування визначених інтегралів
Геометричний зміст визначеного інтеграла — це площа криволінійної фігури (криволінійної трапеції), обмеженої віссю абсцис, двома вертикалями на краях відрізка і кривою графіка функції. (здесь надо нарисовать) Якщо інтегрована на відрізку а<х<Ь функціяДх) невід'ємна, то визначений інте-ь грал f(x)dx чисельнодорівнює площі Sкриволінійної трапеції Уточнимо, що криволінійною трапецісю називають фігуру, обмежену графі-ком неперервної функції у = flx), деДх)>0, прямими х — а, х — Ь та віссю ОХ. Отже, геометричний зміст визначеного інтегралу- це площа криволінійної тра-пеції. Розглянемо криволінійну трапецію CHKD (див. рис. 2), в якої абсциса точки С рівнах, аточки/)-х+/іх. Графік функціїу = flx) перетинає вісь ОГвточці^. Тоді площа криволінійної трапеції CHKD рівна різниці площ криволінійних трапецій OAKD і ОАНС. (а тут 2 каких-то линий байді) Невласні інтеграли Нехай f(x) інтегровна для будь-якого скінченного b Î[a;+¥), так що Означення: Границя
Якщо ця границя скінченна, то невластивий інтеграл називається збіжним, а якщо не існує (в тому числі нескінченна), – розбіжним. Вважаючи, що f(x) – інтегровна для скінченних a та b, формули для обчислення невластивих інтегралів на нескінченному проміжку мають вигляд:
де с=const. Теорема: Якщо при x ³ a має місце нерівність 0£f(x)£g(x) то із збіжності інтеграла Диференціальні рівняння першого порядку Означення: Диф. Рівнянням називається рівняння, яке містить шукану похідну ф-ції. Найбільший порядок похідних називається порядком диференційного рівняння. Лінійні Д.Р. І порядку. Означення: Д.Р. виду y’+P(x)y=Q(x) називається лінійним Д.Р. Якщо Q(x)¹0, то Д.Р. є однорідним, якщо Q(x)º0, то неоднорідним.
Рішення лінійного Д.Р. І порядку: y'+P(x)y=Q(x) y=uv y’=u’v+v’u u’v+v’u+P(x)uv=Q(x) u’v+u(v’+P(x)v)=Q(x) v’+P(x)v=0 u’v=Q(x)
Диференціальні рівняння з відокремлювальними змінними і рівняння, що до них зводяться
Рівняння g(y)=0 досліджується окремо.
Однорідні диференціальні рівняння першого порядку
Неоднорідні диференціальні рівняння першого порядку.
Рівняння вигляду
Звідси Проінтегрувавши, одержимо
І загальний розв’язок неоднорідного рівняння має вигляд
Метод варіації довільної сталої За методом варіації довільної сталої спочатку розв’язують лінійне однорідне рівняння
Рівняння (2) є загальним розв’язком (1), причому частинний розв’язок Загальний розв’язок лінійного неоднорідного рівняння шукають у вигляді Де Тоді
Звідки Отже, загальний розв’язок лінійного неоднорідного рівняння має вигляд:
де перший доданок є загальним розв’язком лінійного однорідного рівняння, а другий – частинним розв’язком лінійного неоднорідного рівняння. Метод Бернуллі За методом Бернуллі шукають загальний розв’язок лінійного неоднорідного рівняння у вигляді
Шукають Рівняння у повних диференціалах. Інтегрувальний множник
|
|||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 511; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.70.93 (0.007 с.) |
 існує.
існує.

 виходить збіжність інтеграла
виходить збіжність інтеграла  , або із розбіжності
, або із розбіжності  випливає розбіжність
випливає розбіжність  .
.


 називається лінійними неоднорідними відносно змінної
називається лінійними неоднорідними відносно змінної  у диференціальному рівнянні першого порядку.Розв’язок неоднорідного рівняння будемо шукати методом варіації довільних сталих (методом невизначених множників Лагранжа). Він складається в тому, що розв’язок неоднорідного рівняння шукається в такому ж вигляді, як і розв’язок однорідного, але
у диференціальному рівнянні першого порядку.Розв’язок неоднорідного рівняння будемо шукати методом варіації довільних сталих (методом невизначених множників Лагранжа). Він складається в тому, що розв’язок неоднорідного рівняння шукається в такому ж вигляді, як і розв’язок однорідного, але  вважається невідомою функцією від
вважається невідомою функцією від  , тобто
, тобто  і
і 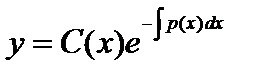 . Для знаходження
. Для знаходження  підставимо
підставимо  у рівняння
у рівняння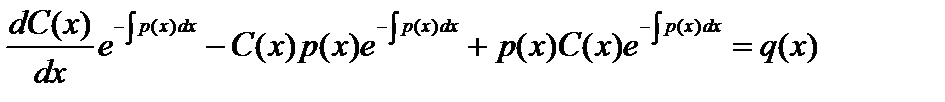
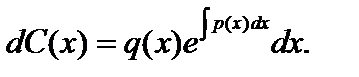
 .
.
 (1), яке є рівнянням з відокремленими змінними, тому при
(1), яке є рівнянням з відокремленими змінними, тому при  мають
мають ;
;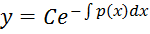 (2)
(2) міститься у ньому при
міститься у ньому при 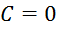 .
.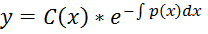 (3)
(3)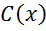 - невідома диференційована функція. Диференціюючи (3) мають:
- невідома диференційована функція. Диференціюючи (3) мають: 
 ,
, ;
;  ;
;
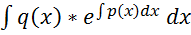 ,
, , де
, де  - невідомі диференційовані функції. Враховуючи співвідношення
- невідомі диференційовані функції. Враховуючи співвідношення  , рівняння
, рівняння 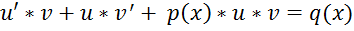 , звідки
, звідки ,(1)
,(1) як розв’язок рівняння з відокремленими змінними
як розв’язок рівняння з відокремленими змінними  , звідки
, звідки  . Обирають значення довільної сталої
. Обирають значення довільної сталої  та повертаються до рівняння (1), підставивши в нього знайдену функцію
та повертаються до рівняння (1), підставивши в нього знайдену функцію  , звідки
, звідки  . Остаточно, враховуючи
. Остаточно, враховуючи 






