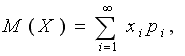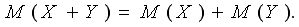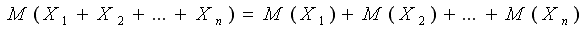Закон плотности распределения вероятностей

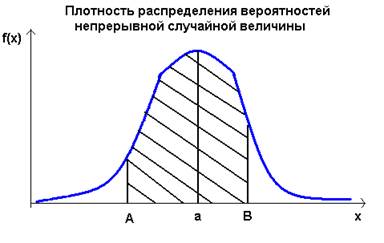
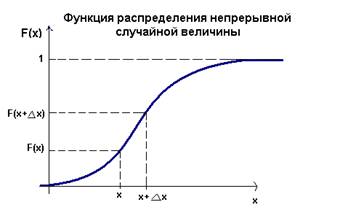
Плотность вероятности - это некоторая средняя вероятность, приходящая на бесконечно малый отрезок

Если это предел существует, то он равен производной от функции распределения F(x):

lim_{Δx →0}(F(x+Δx)-F(x))/Δx)=F'(x)=f(x).

Функция f(x) называется плотностью распределения вероятностей случайной величины Х.

Из определения следует, что при малых значениях Δx справедливо равенство:

P{x≤X<x+Δx}≈f(x)*Δx

Свойства функции плотности распределения вероятности

1. Всегда f(x)≥0, так как функция F(x) является неубывающей функцией.

2 Для функции распределения F(x) справедливо равенство:

F(x)=_-∞∫^xf(t)dt.

Действительно, так как по определению f(x)=F'(x), то F(x) является первообразной функцией по отношению к плотности распределения f(x). Следовательно,

_-∞∫^∞f(t)dt=F(t)_-∞ι^x=F(x)-F(-∞)=F(x)-0=F(x.)

3. Вероятность попадания случайной величины в заданный интервал [Α; Β] равна:

P{Α≤X<Β}=_Α∫^βf(t)dt.

Действительно, в соответствии с формулой Ньютона-Лейбница этот определенный интеграл равен F(Β)-F(Α). По 3-му свойству функции распределения вероятностей эта разность и представляет собой вероятность P{Α≤X<Β}.

4. Интеграл от плотности распределения вероятности по всей области задания случайной величины равен единице:

_-∞∫^∞f(t)dt=1.

Равенство _-∞∫^∞f(t)dt=1 представляет условие нормировки вероятностей для непрерывных случайных величин. По смыслу данный интеграл есть не что иное, как F(∞)=1. Условие нормировки вероятностей часто используется для определения неизвестного параметра закона распределения.

Для иллюстрации геометрического смысла перечисленных свойств приведем пример графика плотности распределения вероятностей. Для большей наглядности на рис. представлен также график соответствующей функции распределения вероятностей.

Вся кривая плотности распределения вероятностей располагается выше оси 0Х (свойство1), причем максимум плотности достигается в точке х=а, в которой функция распределения вероятностей имеет наибольшую крутизну. Вероятность попадания случайной величины в интервал [Α; Β] численно равна площади криволинейной трапеции, построенной на этом интервале как на основании и ограниченной сверху графиком плотности распределения (заштрихованная на рисунке область). Площадь всей криволинейной трапеции, заключенной между осью 0Х и графиком плотности распределения, всегда равна единице. Любая функция, удовлетворяющая перечисленным выше свойствам, может быть плотностью распределения некоторой непрерывной случайной величины.

Числовые характеристики случайной величины.

Случайная величина — это величина, которая принимает в результате опыта одно из множества значений, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать.

Числовыми характеристиками случайных величин являются математическое ожидание и дисперсия, а так же и моменты случайных величин

 

Математическое ожиданием М(Х) называется средняя величина возможных значений случайных величин, взвешенных по их вероятности. Выражается формулой:

 

Дисперсией называется математическое ожидание квадрата отклонения случайных величин от математического ожидания:

D[Х]=M[X-M(X)]²

 

Свойства математического ожидания.

Математическое ожиданием М(Х) называется средняя величина возможных значений случайных величин, взвешенных по их вероятности. Выражается формулой:

Свойство 1. Мат. ожидание постоянной равно этой постоянной.

 

Свойство 2. Мат. ожидание суммы случайных величин равно сумме их мат. ожиданий:

 

Из этого свойства следует следствие:

Математическое ожидание суммы конечного числа случайных величин равно сумме их математических ожиданий:

 

Свойство 3. Математическое ожидание произведения независимых случайных величин Х и Y равно произведению математических ожиданий этих вел. M(XY)=M(X)·(M)Y.

 

Следствие. Постоянный множитель можно вынести за знак математических ожидания: М(сХ) = сМ(Х)

Дисперсия и ее свойства.

Дисперсией называется математическое ожидание квадрата отклонения случайных величин от математического ожидания:

D[Х]=M[X-M(X)]²

 

Свойство 1. Дисперсия постоянной величины равна нулю.

 

Свойство 2. постоянную величину можно вынести за знак дисперсии, предварительно возведя ее в квадрат:

D(cX) = c²D(X)

 

Свойство 3. Дисперсия суммы независимых случайных величин Х и Y равна сумме их дисперсий:

D(X+Y) = D(X) + D(Y), от сюда следствие:

 

если х₁, х₂,..., х_n - случайные величины, каждая из которых независима от суммы остальных, то

D(X₁+X₂+...+X_n) = D(X₁) + D(X₂)+...+D(X_n).

 

Моментом k -порядка называется математическое ожидание k -й степени отклонения случайной величины Х от некоторой постоянной с.

 

Если в качестве с берется нуль, моменты называются начальными

ν_k = М(Х)^k

 

Если с = М(Х), то моменты называются центральными

μ = M[X – M(X)]^k