
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства функции распределения.Стр 1 из 6Следующая ⇒
Понятие случайной величины. В самом общем смысле случайная величина - это некоторая переменная, принимающая, те или иные значения с определенными вероятностями. Случайная величина - это величина, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены. Гистограмма - один из способов представления случайной величины. случайная величина может быть: 2. Закон распределения вероятностей дискретной случайной величины Законом распределения дискретной случайной величины называют соответствие между возможными значениями случайной величины и вероятностями их появления. Закон распределения можно задать таблично, аналитически (в виде формулы) или графически (в виде многоугольника распределения). Рассмотрим случайную величину X, которая принимает значения x1, x2, x3 ... xn с некоторой вероятностью pi, где i = 1.. n. Сумма вероятностей pi равна 1.
Таблица соответствия значений случайной величины и их вероятностей вида
называется рядом распределения дискретной случайной величины или просто рядом распределения. Эта таблица является наиболее удобной формой задания дискретной случайной величины. Графическое представление этой таблицы называется многоугольником распределения. По оси абсцисс откладываются возможные значения дискретной случайной величины, а по оси ординат соответствующие вероятности. Закон Бернулли
Закон распределения Пуассона
Функция распределения Фу́нкция распределе́ния — функция, характеризующая распределение случайной величины или случайного вектора. Для количественной характеристики этого распределения вероятностей удобно воспользоваться не вероятностью события
Свойства функции распределения. 1. Функция распределения 2. На минус бесконечности функция распределения равна нулю: 3. На плюс бесконечности функция распределения равна единице:
Любая функция распределения обладает следующими свойствами: (F1) она не убывает: если (F2) cуществуют пределы (F3) она в любой точке непрерывна слева: Закон плотности распределения вероятностей Плотность вероятности - это некоторая средняя вероятность, приходящая на бесконечно малый отрезок Если это предел существует, то он равен производной от функции распределения F(x): limΔx →0(F(x+Δx)-F(x))/Δx)=F'(x)=f(x). Функция f(x) называется плотностью распределения вероятностей случайной величины Х. Из определения следует, что при малых значениях Δx справедливо равенство: P{x≤X<x+Δx}≈f(x)*Δx Дисперсия и ее свойства. Дисперсией называется математическое ожидание квадрата отклонения случайных величин от математического ожидания: D[Х]=M[X-M(X)]2
Свойство 1. Дисперсия постоянной величины равна нулю.
Свойство 2. постоянную величину можно вынести за знак дисперсии, предварительно возведя ее в квадрат: D(cX) = c2D(X)
Свойство 3. Дисперсия суммы независимых случайных величин Х и Y равна сумме их дисперсий: D(X+Y) = D(X) + D(Y), от сюда следствие:
если х1, х2,..., хn - случайные величины, каждая из которых независима от суммы остальных, то D(X1+X2+...+Xn) = D(X1) + D(X2)+...+D(Xn).
Моментом k -порядка называется математическое ожидание k -й степени отклонения случайной величины Х от некоторой постоянной с.
Если в качестве с берется нуль, моменты называются начальными νk = М(Х)k
Если с = М(Х), то моменты называются центральными μ = M[X – M(X)]k Моменты случайной величины. Момент случайной величины — числовая характеристика распределения данной случайной величины. Если дана случайная величина
если математическое ожидание
если математическое ожидание в правой части этого равенства определено. Замечания Если определены моменты В силу линейности математического ожидания центральные моменты могут быть выражены через начальные, и наоборот. Например:
Вычисление моментов Моменты могут быть вычислены напрямую через определение путём интегрирования соответствующих степеней случайной величины. В частности, для абсолютно непрерывного распределения с плотностью
если а для дискретного распределения с функцией вероятности
если Также моменты случайной величины могут быть вычислены через ее характеристическую функцию
Если распределение таково, что для него в некоторой окрестности нуля определена производящая функция моментов
Биномиальное распределение. Биномиальное распределение распределение вероятностей числа появлений некоторого события при повторных независимых испытаниях. Если при каждом испытании вероятность появления события равна р, причём 0 ≤ p ≤ 1, то число μ появлений этого события при n независимых испытаниях есть случайная величина, принимающая значения m = 1, 2,.., n с вероятностями
где q = 1 — p, a Распределение Пуассона. Распределение Пуассона — вероятностное распределение дискретного типа, моделируетслучайную величину , представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.Распределение Пуассона играет ключевую роль в теории массового обслуживания. Выберем фиксированное число
где · · Тот факт, что случайная величина Функция распределения Интегрируя плотность, получаем функцию экспоненциального распределения:
Моменты Несложным интегрированием находим, что производящая функция моментов для экспоненциального распределения имеет вид:
Закон распределения системы случайных величин. Таблица распределения. (в файле 2) Законом распределения системы случайных величин называется соотношение, устанавливающее связь между областями возможных значений системы случайных величин и вероятностями появления системы в этих областях.[/b]
Так же, как и для одной случайной величины, закон распределения системы случайных величин может быть задан в различных формах. Рассмотрим таблицу распределения вероятностей системы дискретных случайных величин. Пусть
Такая таблица называется таблицей распределения системы двух дискретных случайных величин с конечным числом возможных значений. Все возможные события
При этом
Свойство 1.
или символически
Свойство 2.
Свойство 3.
или
Свойство 4. Функция распределения является неубывающей функцией по каждому аргументу:
Свойство 5. Вероятность попадания случайной точки
Распределение одной случайной величины, входящей в систему, найденное при условии, что другая случайная величина, входящая в систему, приняла определенное значение, называется условным законом распределения.
Условный закон распределения можно задавать как функцией распределения, так и плотностью распределения. Условная функция распределения обозначается
Плотностью распределения для случайной величины
Аналогично плотностью распределения для случайной величины
Условная плотность распределения обладает всеми свойствами безусловной плотности распределения. В частности,
24. Числовые характеристики системы двух случайных величин. Корреляционный момент. Коэффициент корреляции. 25. Центральным моментом порядка s, h системы СВ (X, Y) называется математическое ожидание произведения степеней s, h соответствующих центрированных случайных величин:
Вторые центральные моменты: Коэффициент корреляции служит мерой линейной зависимости между случайными величинами.
25. Неравенство Чебышева. Нера́венство Чебышёва в теории вероятностей утверждает, что случайная величина в основном принимает значения близкие к своему среднему. Более точно, оно даёт оценку вероятности, что случайная величина примет значение далёкое от своего среднего. Неравенство Чебышёва является следствием неравенства Маркова. Формулировки Пусть случайная величина
Если
Метод наименьших квадратов является одним из наиболее распространенных и наиболее разработанных вследствие своей простоты и эффективности методов оценки параметров линейных эконометрических моделей. Вместе с тем, при его применении следует соблюдать определенную осторожность, поскольку построенные с его использованием модели могут не удовлетворять целому ряду требований к качеству их параметров и, вследствие этого, недостаточно “хорошо” отображать закономерности развития процесса Рассмотрим процедуру оценки параметров линейной эконометрической модели с помощью метода наименьших квадратов более подробно. Такая модель в общем виде может быть представлена уравнением (1.2): yt = a0 + a1 х1t +...+ an хnt + εt. Исходными данными при оценке параметров a0 , a1 ,..., an является вектор значений зависимой переменной y = (y1, y2,..., yT)' и матрица значений независимых переменных
в которой первый столбец, состоящий из единиц, соответствует коэффициенту модели Название свое метод наименьших квадратов получил, исходя из основного принципа, которому должны удовлетворять полученные на его основе оценки параметров: сумма квадратов ошибки модели должна быть минимальной. Статистической гипотезой Определения Пусть в (статистическом) эксперименте доступна наблюдению случайная величина
На практике обычно требуется проверить какую-то конкретную и как правило простую гипотезу Выдвинутая гипотеза нуждается в проверке, которая осуществляется статистическими методами, поэтому гипотезу называют статистической. Для проверки гипотезы используют критерии, позволяющие принять или опровергнуть гипотезу. В большинстве случаев статистические критерии основаны на случайной выборке
\ Понятие случайной величины. В самом общем смысле случайная величина - это некоторая переменная, принимающая, те или иные значения с определенными вероятностями. Случайная величина - это величина, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены. Гистограмма - один из способов представления случайной величины. случайная величина может быть: 2. Закон распределения вероятностей дискретной случайной величины Законом распределения дискретной случайной величины называют соответствие между возможными значениями случайной величины и вероятностями их появления. Закон распределения можно задать таблично, аналитически (в виде формулы) или графически (в виде многоугольника распределения). Рассмотрим случайную величину X, которая принимает значения x1, x2, x3 ... xn с некоторой вероятностью pi, где i = 1.. n. Сумма вероятностей pi равна 1.
Таблица соответствия значений случайной величины и их вероятностей вида
называется рядом распределения дискретной случайной величины или просто рядом распределения. Эта таблица является наиболее удобной формой задания дискретной случайной величины. Графическое представление этой таблицы называется многоугольником распределения. По оси абсцисс откладываются возможные значения дискретной случайной величины, а по оси ординат соответствующие вероятности. Закон Бернулли Закон распределения Пуассона
Функция распределения Фу́нкция распределе́ния — функция, характеризующая распределение случайной величины или случайного вектора. Для количественной характеристики этого распределения вероятностей удобно воспользоваться не вероятностью события
Свойства функции распределения. 1. Функция распределения 2. На минус бесконечности функция распределения равна нулю: 3. На плюс бесконечности функция распределения равна единице:
Любая функция распределения обладает следующими свойствами: (F1) она не убывает: если (F2) cуществуют пределы (F3) она в любой точке непрерывна слева:
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 641; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.42.196 (0.135 с.) |

 - число сочетаний из n элементов по m.
- число сочетаний из n элементов по m.
 , а вероятностью события
, а вероятностью события  , где
, где  – некоторая текущая переменная. Вероятность этого события, очевидно, зависит от
– некоторая текущая переменная. Вероятность этого события, очевидно, зависит от  и обозначается
и обозначается  :
: . (5.2.1)
. (5.2.1)
 .
. .
. .
. , то
, то  ;
; и
и  ;
;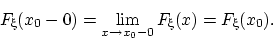
 определённая на некотором вероятностном пространстве, то:
определённая на некотором вероятностном пространстве, то: -м начальным моментом случайной величины
-м начальным моментом случайной величины  называется величина
называется величина
 в правой части этого равенства определено;
в правой части этого равенства определено; называется величина
называется величина





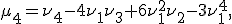 и т. д.
и т. д.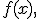 имеем:
имеем:



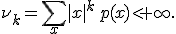
 :
:
 то моменты могут быть вычислены по следующей формуле:
то моменты могут быть вычислены по следующей формуле:

 — биномиальные коэффициенты (отсюда название Б. р.). Приведённая формула иногда называется формулой Бернулли. Математическое ожидание и Дисперсия величины μ, имеющей Б. р., равны М (μ) = np и D (μ) = npq, соответственно. При больших n, в силу Лапласа теоремы (См. Лапласа теорема), Б. р. близко к нормальному распределению (См. Нормальное распределение), чем и пользуются на практике. При небольших n приходится пользоваться таблицами Б. р.
— биномиальные коэффициенты (отсюда название Б. р.). Приведённая формула иногда называется формулой Бернулли. Математическое ожидание и Дисперсия величины μ, имеющей Б. р., равны М (μ) = np и D (μ) = npq, соответственно. При больших n, в силу Лапласа теоремы (См. Лапласа теорема), Б. р. близко к нормальному распределению (См. Нормальное распределение), чем и пользуются на практике. При небольших n приходится пользоваться таблицами Б. р. и определим дискретное распределение, задаваемое следующей функцией вероятности:
и определим дискретное распределение, задаваемое следующей функцией вероятности: ,
, обозначает факториал числа
обозначает факториал числа 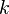 ,
, — основание натурального логарифма.
— основание натурального логарифма.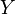 имеет распределение Пуассона с параметром
имеет распределение Пуассона с параметром  , записывается:
, записывается:  .
.
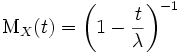 ,
,
 и
и  — дискретные случайные величины, возможные значения которых
— дискретные случайные величины, возможные значения которых  , где
, где  Тогда распределение системы таких случайных величин может быть охарактеризовано указанием вероятностей
Тогда распределение системы таких случайных величин может быть охарактеризовано указанием вероятностей  того, что случайная величина
того, что случайная величина  и одновременно с этим случайная величина
и одновременно с этим случайная величина 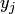 . Вероятности
. Вероятности  фиксируют в таблице.
фиксируют в таблице. при
при 
 составляют полную группу несовместных событий, поэтому
составляют полную группу несовместных событий, поэтому


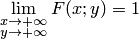 или
или 

 в произвольный прямоугольник со сторонами, параллельными координатным осям (рис. 15), вычисляется, по формуле
в произвольный прямоугольник со сторонами, параллельными координатным осям (рис. 15), вычисляется, по формуле
 , условная плотность распределения —
, условная плотность распределения —  (мы записали условные законы распределения случайной величины
(мы записали условные законы распределения случайной величины 
 . Отсюда получаем
. Отсюда получаем  .
.


 :
:

 - характеризует рассеяние случайных величин в направлении оси OX.
- характеризует рассеяние случайных величин в направлении оси OX. - характеризует рассеяние случайных величин в направлении оси OY.
- характеризует рассеяние случайных величин в направлении оси OY.
 , отсюда
, отсюда 
 где
где 

 , то случайные величины линейно зависимы;
, то случайные величины линейно зависимы; , то случайные величины не коррелированны, что не означает их независимости вообще.
, то случайные величины не коррелированны, что не означает их независимости вообще. определена на вероятностном пространстве
определена на вероятностном пространстве  , и её математическое ожидание
, и её математическое ожидание  и дисперсия
и дисперсия  конечны. Тогда
конечны. Тогда , где
, где  .
. , где
, где  - стандартное отклонение и
- стандартное отклонение и  , то получаем
, то получаем В частности, случайная величина с конечной дисперсией отклоняется от среднего больше, чем на
В частности, случайная величина с конечной дисперсией отклоняется от среднего больше, чем на  стандартных отклонения с вероятностью меньше
стандартных отклонения с вероятностью меньше  . Она отклоняется от среднего на
. Она отклоняется от среднего на  стандартных отклонения с вероятностью меньше
стандартных отклонения с вероятностью меньше  .
. .
.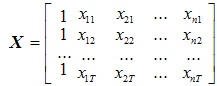
 .
. , распределение которой
, распределение которой  известно полностью или частично. Тогда любое утверждение, касающееся
известно полностью или частично. Тогда любое утверждение, касающееся  называется статистической гипотезой. Гипотезы различают по виду предположений, содержащихся в них:
называется статистической гипотезой. Гипотезы различают по виду предположений, содержащихся в них: , где
, где  какой-то конкретный закон, называется простой.
какой-то конкретный закон, называется простой.  , где
, где  — семейство распределений, называется сложной.
— семейство распределений, называется сложной. 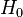 . Такую гипотезу принято называть нулевой. При этом параллельно рассматривается противоречащая ей гипотеза
. Такую гипотезу принято называть нулевой. При этом параллельно рассматривается противоречащая ей гипотеза  , называемая конкурирующей или альтернативной.
, называемая конкурирующей или альтернативной. фиксированного объема
фиксированного объема  из распределения
из распределения 


