
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Орнаменты на сфере. Изогнутые крыши
При создании симметричных орнаментов на потолке, имеющем форму круглого купола (полусферы или четверти сферы, венчающей нишу полукруглой формы), приходится учитывать, что длина "параллелей" по мере приближения к вершине сферы (ее "северному полюсу") уменьшается. Такая же проблема возникает при покрытии листами одинаковой формы изогнутых крыш - маковок церквей, куполов и т.д.
На рисунке 13а приведен чертеж, помогающий понять, как провести предлагаемое построение. Пусть купол, имеющий ось вращения ОD и длину основания L (будем называть его "экватором"), поделен на n частей. В этом случае длина дуги по экватору между соседними "меридианами" D0=L/n. Для того чтобы получить на сфере купола первый пояс квадратов (вернее трапеций), надо вдоль меридиана отложить дугу, длина которой равна D0. Для того чтобы получить на чертеже длину D0, радиусом ОА0 проведем окружность, поделим ее на n частей и проведем хорду А0С0 (если купол окружность, то его линию можно взять в качестве этой вспомогательной окружности и точки А1 и С0 совпадут). Измерим ее хорду циркулем и отложим это расстояние от точки А0 вверх по линии купола. Обозначим конечную точку дуги через А1. Радиус полученной параллели меньше, чем радиус "экватора". Из точки А1 опустим перпендикуляр на ОА0. Основание перпендикуляра обозначим через В1. ОВ1 – длина этого радиуса. Проведем дугу окружности такого радиуса до пересечения с радиусом ОС1. Длина дуги (вернее, хорды) D1=В1С1. Измеряем эту длину циркулем и откладываем ее от точки А1 вверх по дуге купола. Получаем точку А2. Опускаем из нее перпендикуляр, получаем точку В2. Проводим дугу радиуса ОВ2, получаем длину хорды D2=В2С2, откладываем эту длину от точки А2 вверх по линии купола и далее продолжаем процесс по этой же схеме.
Если купол – полусфера радиуса r0, можно вычислить "широту" ai построенных параллелей. Задав начальные данные для построения (в этой схеме ничего не надо знать, кроме числа частей n, на которое делится экватор), можно провести расчеты для вычисления этих широт. Приведем пример такого расчета. Пусть купол, радиус которого равен r, поделен на n=24 части. В этом случае угол между "меридианами" равен 360°:n=360°:24=15°=2p/24 и длина дуги по экватору между соседними меридианами D0=2pr/24. Следовательно, для того, чтобы получить на сфере купола первый пояс квадратов (трапеций), надо вдоль меридиана отложить дугу, длина которой равна D0=2pr/24=rp/12. Обозначим конечную точку дуги через А1, а широту этой параллели через a1. Длина параллели на этом уровне будет в cosa1 раз меньше, чем длина "экватора". Если радиус экватора равен r=r0, то радиус первой параллели r1=r0cosa1, (a1=15°=p/12). Следовательно, для построения следующего пояса "квадратной" сетки, надо вдоль меридиана отложить длину дуги, равную: D1=2pr1/24=r1×p/12=r0×p/12×cosa1=r0×p/12×cosp/12=r0a1cosa1=D0cosa1. Из точки А1 опускаем перпендикуляр на радиус ОА0. Основание перпендикуляра обозначим через В1. ОВ1=r1=r0cosa1. Проводим дугу окружности такого радиуса до пересечения с радиусом ОА1. Длина дуги (и хорды) D1=В1С1=D0cosa1. Измеряем эту длину циркулем и откладываем ее от точки А1 вверх по дуге окружности. Получаем точку А2. Опускаем из нее перпендикуляр, получаем точку В2. ОВ2=r2=r0cosa2. Проводим дугу радиуса ОВ2, получаем длину хорды D2=В2С2, откладываем эту длину от точки А2 вверх по окружности и далее процесс продолжаем по этой же схеме. По мере построения новых поясов орнамента ширина полосы становится все меньше и, не доходя до полюса, орнамент, ставший слишком мелким, обычно заканчивают, поместив в центре потолка красивую розетку.
Выведем формулу для вычисления значения углов a1, a2,…- широт, на которых расположены построенные параллели. Значение a1 определяется по n: a1=2p/n (в радианах). Значение a2 вычисляется по a1 по формуле: a2=a1+a1cosa1. Действительно, вспомним, что величина угла a в радианах и опирающаяся на него дуга D связаны простым соотношением: D=ra, где r – радиус окружности. На угол a2. опирается сумма 2-х дуг: ra2=D0+D1=ra1+ra1cosa1, откуда и получаем: a2=a1+a1cosa1. Аналогично, так как на i-ом шагу дуга наращивается на величину D0cosai-1=ra1cosai-1, ai=ai-1+a1cosai-1 (см. рис.13б). По начальному значению a1=2p/n и по формуле ai=ai-1+a1cosai-1 для i>1 можно последовательно вычислить значения an для любого n. Формулы, выражающие какую-либо величину, зависящую от числа n, через ту же величину при меньшем абсолютном значении n, называются рекуррентными, или возвратными. Таким образом, мы применили метод расчета (и последовательный пошаговый метод построения) по рекуррентной формуле. Ранее мы уже встречались с этим методом. С помощью рекуррентной формулы an=an-1+an-2 по заданным начальным значениям a1 и a2 вычисляются значения n-ого члена рассмотренных нами последовательностей - Фибоначчи (a1=1, a2=1) и Люка (a1=1, a2=3). Эти последовательности являются возвратными. Расчет по приведенным формулам для n=24 при переводе значения угла в привычную градусную меру дал следующие значения для углов a1, a2, a3,…: a1=15°, a2=29,5°, a3=42,5°, a4=53,5°, a5=62,5°,… Приведем пример таблицы подобного расчета. Таблица расчета полос для сетки с шагом 15°
До широты 60° простирается 5 полос, а не 4, как было бы, если бы полосы все имели одинаковую ширину 60°:15°=4. И если на первых двух полосах разница почти незаметна, то после третьей полосы начинается их быстрое сужение и орнамент кончают. В римском Пантеоне кверху простирается 5 поясов "квадратов" (в последнем поясе линейные размеры квадратов примерно вдвое меньше, чем в первом), в центре потолка круглое отверстие диаметром 9м, через которое проникают солнечные лучи. Подобная сетка является основой для любого орнамента на сфере, требующего сохранения "подобия" фигур, построенных в ячейках пояса, при переходе к следующим поясам. Чаще всего это розетки, радиус которых уменьшается при приближении к "полюсу", прямоугольники, немного сужающиеся кверху (то есть трапеции), ромбы, (одна из диагоналей идет вдоль параллелей, другая – по меридиану). Для того чтобы искривление не было заметно, их располагают не вплотную друг к другу. Если построить на сфере по этому принципу сетку с маленьким шагом, то она может послужить основой для построения достаточно сложных орнаментов, подчиняющихся принципам симметрии и подобия.
М. Эшер
Сфера является объектом, который трудно поддается переводу на плоскость. Ее нельзя, как мы уже говорили, разложить на плоскости. При создании географических карт прибегают к разным видам проекций сферы на плоскость. Есть проекции, сохраняющие размеры по параллелям, или сохраняющие углы, или сохраняющие площади (этой проекцией мы воспользовались, когда вычисляли площадь поверхности сферы) и т.д. Один вид проекции удобен в одном случае, другой в другом. Параллельная и центральная проекции. На рисунке 14 изображена самая простая - параллельная ортогональная проекция полусферы на плоскость (пучок параллельных прямых ортогонален плоскости экватора). Радиус проекции экватора равен радиусу полусферы. Параллели переходят в концентрические окружности того же радиуса. Меридианы переходят в прямые, пересекающиеся в проекции полюса. Такая проекция устанавливает взаимно однозначное соответствие между точками полусферы и точками круга, радиус которого равен радиусу полусферы. Сохраняя длины вдоль параллелей, такая параллельная проекция искажает длины вдоль меридианов. Половина меридиана длины pR переходит в отрезок прямой длины 2R, причем искажение неравномерно. Если спроектировать часть земной поверхности, прилегающую к полюсу, из центра Земли на плоскость, касающуюся земной поверхности в северном полюсе (центральная проекция), то меридианы перейдут в прямые, параллели в окружности (рис. 15).
Радиус окружности параллели равен Rcosa=Rsinq. Радиус окружностей их проекций вычисляется по формуле: r=Rtgq=Rctga (a=90-J, a - географическая широта, q - угол с вертикалью в сферической системе координат). Чем ближе q к 90° (параллель к экватору), тем больше радиус окружности. Так что центральная проекция устанавливает взаимно однозначное соответствие между полусферой и плоскостью. Экватору соответствует бесконечно удаленная точка плоскости. Такая проекция искажает размеры и по параллелям и по меридианам. Но она удобна летчикам, летающим в высоких широтах. Путь самолета выгоднее всего прокладывать по дугам больших кругов - так называемым ортодромам (по ним проходит кратчайший путь между любыми двумя точками, лежащими на сфере). А при центральной проекции все ортодромы переходят в прямые линии (линии пересечения плоскости, проходящей через центр Земли и ортодрому с плоскостью проекции). И на карте Арктики, полученной с помощью центральной проекции, путь самолета - это прямая.
Стереографическая проекция. Построим проекцию купола на плоский потолок – на плоскость, проходящую через экватор, взяв в качестве центра проекции "южный" полюс (рис. 16а). На рисунке 16б изображен боковой разрез этой проекции. Меридианы перейдут в прямые, пересекающиеся в проекции центра купола (рис. 16в). Параллель, южная широта которой равна a=90-q, где q - угол с вертикалью, проектируется в окружность, радиус которой равен ОА=Rtgq/2= С математической точки зрения, если глаза наблюдателя помещаются в южном полюсе купола, то ему безразлично, нарисован орнамент на куполе или на плоском потолке нарисована его стереографическая проекция.
Мы говорили о важном свойстве логарифмических спиралей – они пересекают прямые, выходящие из центра, под одним и тем же углом. Кривые, лежащие на сфере, пересекающие меридианы под одним и тем же углом называются локсодромами. Путь по локсодроме удобен мореплавателю, который выбрал свой курс по компасу и сохраняет этот курс неизменным. Такой мореплаватель плывет по локсодроме. Движение по локсодроме очень удобно для управления кораблем, хотя такой способ прокладывания курса удлиняет путь. Кратчайший путь между двумя точками на шаре - движение по дуге большого круга, проходящей через эти точки (по ортодромам). В силу свойства сохранения углов стереографической проекцией локсодром будут логарифмические спирали.
Задачи для самостоятельного решения 1. Даны два вектора 2. На координатной плоскости заданы точки А(-1,3), В(2,-5), С(3,4). Найдите координаты векторов 3. Дан параллелограмм ABCD. Найдите 4. Нарисовать на круге узор из спиралей Архимеда (n=16). 5. Нарисовать на круге узор из логарифмических спиралей (сетка на основе подобия, n=16). Вычислить значения геометрической прогрессии для радиусов. 6. Начертить параллельную проекцию северного полушария вниз на горизонтальную плоскость, обозначить на проекции меридианы и параллели с шагом 22°30'. 7. Провести расчет широт полос на полусфере по приведенной таблице еще для одной полосы и построить чертеж разреза купола. 8. Рассчитать таблицу для 4 полос сетки на полусфере, если ширина первой полосы 20°. Начертить разрез этой полусферы
М.Эшер. Сетка на шаре, локсодрома
Функции и графики Понятие функции Пусть Е есть множество чисел и пусть в силу некоторого вполне определенного закона каждому числу х из Е приведено в соответствие одно число у. Тогда говорят, что на Е задана функция, которую записывают так: y=f(x).
Это определение функции предложено Лобачевским и Дирихле (XIX век). Множество Е называется областью задания или областью определения функции f(x), х называют независимой переменной. Функция может быть задана и в неявном виде уравнением F(x,y)=0, не разрешенным относительно у. Например, уравнение х2+у2=R2, которое можно переписать в форме х2+у2-R2=0, задает неявную функцию у (уравнение y=f(x) задает функцию в явном виде). Если функция задается только с помощью аналитического выражения без каких-либо дополнительных условий, то под ее областью определения понимают совокупность всех тех значений аргумента, для которых это выражение имеет смысл. Например, для функции y=sinx областью определения является вся числовая прямая, а для функции Некоторые важные свойства функций имеют специальные наименования. Четные и нечетные функции. Функция y=f(x) называется четной, если f(-x)=f(x) для всех х из области определения. График четной функции симметричен относительно оси ординат (OY).
Примеры y=x2(рис. 1а) - четная функция, так как (-x)2=x2. Вообще, четными являются функции y=x2n при любом натуральном n (то есть степенные функции с четной степенью). y=cosx – четная функция, так как cos(-x)=cosx
Функция y=f(x) называется нечетной, если f(-x)=-f(x) для всех х из области определения. График нечетной функции симметричен относительно начала координат.
Примеры y=x3(рис. 1б) – нечетная функция, так как (-x)3=-x3. Нечетными являются функции y=x2n-1 при любом натуральном n (то есть степенные функции с нечетной степенью). y=sinx – нечетная функция, так как sin(-x)=-sinx.
Периодические функции. Функция y=f(x) называется периодической, если существует число Т¹0 такое, что f(x±T)=f(x) в области определения функции (рис. 1в). Наименьшее из таких положительных чисел Т называется периодом.
Примеры y=sinx, y=cosx, y=tgx, y=ctgx – периодические функции. Период первых двух функций равен 2p, вторых двух - p.
График периодической функции достаточно построить на отрезке длины Т, далее построенный кусок кривой надо сдвигать вдоль оси Х на величину периода. Монотонные функции. Если функция y=f(x), определенная на интервале, является только возрастающей (большему значению аргумента х в этом интервале соответствует большее значение функции) или только убывающей на этом интервале (большему значению аргумента х в этом интервале соответствует меньшее значение функции), то она называется монотонной на интервале (рис. 1г).
На рисунке 1 приведены графики функций и отмечены их свойства.
Примеры решения задач. 1. Для функции, значение которой при x³0 вычисляется по формуле y=2x-2 для х£1 и у=0 для х>1, построить симметрию относительно оси OY (функцию, заданную для x³0, доопределить для х<0 из соображений четности - решение на рисунке 2).
2. Для функции, значение которой при x>0 вычисляется по формуле y=1/3x+1 для 0<x<3, y=3 для x³3 (рис. 3), построить симметрию относительно начала координат (доопределить функцию для х<0 из соображений нечетности). 3. Известно, что функция является периодической. По графику, заданному для одного периода (рис. 4а) построить график функции на всей прямой (рис. 4б)
Элементарные функции Основными элементарными функциями называются следующие функции. 1. Степенные функции: у=хa, где a - действительное число.
Ее поведение очень сильно зависит от значения a. а) a=0, y=const (рис. 5а) б) aÎN (натуральное, т.е. целое положительное), функция определена на всей числовой оси. На рисунках. 5б,в,г приведены графики функций у=хa для целых положительных значений a=1, a=2, a=3. в) a - целое отрицательное число; функция определена при всех значениях х¹0 (рис. 6а) г) a - дробное (на рис. 6б,в даны графики степенных функций при a=1/2 и a=1/3).
2. Показательная функция: у= а х определена для всех х и положительна. При а >1 она монотонно возрастает, при 0< a <1 монотонно убывает (рис 7а,б). Для любого а у(0)=а0=1 3. Логарифмическая функция: y=log a x определена для всех x>0. Число а называется основанием логарифма (a >0, a ¹1). Напомним, определение логарифма: На практике часто используются логарифмы по основанию 10. Для них принята сокращенная запись lg. При а >1функция монотонно возрастает, при 0< a <1 монотонно убывает (рис 7в,г). log a 1=0 при любом основании а
В математике особую роль играют показательная и логарифмическая функция с основанием а=е. Число е – иррациональное число. Его можно записать в виде бесконечной непериодической дроби е =2,71828182845… Логарифм по основанию а=е называют натуральным и записывают обычно в виде y=lnx. Показательную функцию y=ex называют экспоненциальной функцией, иногда ее записывают так: у= ехр х. Заметим, что ax=exln a (в силу того, что по определению логарифма a=eln a ). Кроме названия функции, указания операций (+, -, ×,:) и основных величин, обозначаемых через x, y, z,…, в формулу могут входить константы и параметры – константы, значения которых не заданы. Их обычно обозначают латинскими буквами a, b, c,… Например, для функций ах и logax a – это параметр. 4. Тригонометрические функции: y=sinx, y=cosx, y=tgx, y=ctgx. Аргументом является угол в радианах.
Функции y=sinx, y=cosx определены при всех значениях х, функция y=tgx определена на всей числовой оси, кроме точек: x=(2k+1)p/2, (k=0, ±1, ±2,…), функция y=ctgx определена на всей числовой оси, кроме точек: x=kp (k=0, ±1, ±2,…) (рис. 8) 5. Обратные тригонометрические функции: y=arcsinx, y=arccosx, y=arctgx, y=arcctgx. Эти функции являются обратными к тригонометрическим. Функция y=arcsinx определяется следующим образом: по заданному значению sinx=с, определяется у – угол в радианах, синус которого равен заданному значению с ( задана хорда, найти длину дуги ). Функция y=arccosx определяется так: по заданному значению cosx=с, определяется у – угол в радианах, косинус которого равен заданному значению с. Функция y=arctgx: задано значение tgx=с, у – величина угла, тангенс которого равен заданному значению с. Функция y=arcctgx: задано значение ctgx=с, у – величина угла, котангенс которого равен заданному значению с. Обратная функция определяется на интервале, на котором любое ее значение принимается только один раз. При определении функции, обратной к данной, значения функции и аргумента меняются ролями. Проще всего это понять, если задана таблица функции - по значению аргумента таблица позволяет определить значение функции. Эта же таблица может использоваться, как таблица обратной функции. Но тогда ею надо пользоваться по-другому. Среди значений функции надо отыскать значение, самое близкое к тому, которое задано, и в качестве ответа взять из таблицы аргумент, которому соответствует это значение функции. Например, при расчете угла наклона боковой грани египетской пирамиды j, было получено, что tgj=1,35. В Таблице значений тригонометрических функций Приложения находим, что такое значение тангенса соответствует углу, равному примерно 53,5°. Взаимно обратными являются и рассмотренные нами ранее функции: показательная у=ах и логарифмическая y=logax, степенная у=хa и Функции, которые получаются из основных элементарных функций с помощью конечного числа арифметических операций (сложения, вычитания, умножения и деления) и операций подстановки ("взятие функции от функции"), называются элементарными функциями. Например,
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 640; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.222.12 (0.099 с.) |






 Построить на сфере симметричный орнамент из подобных квантов, имеющих форму квадрата (вернее трапеции), можно следующим способом. "Экватор" делится на n равных частей (число на усмотрение создателя орнамента, обычно n=12, 16, 24). Через полученные на экваторе точки проводятся меридианы. По меридиану откладывается длина одной части, полученной на экваторе. На этом уровне проводится первая параллель ("экватор" – нулевая параллель). Получаем первый пояс из фигур, которые являются криволинейными "квадратами". Верхняя сторона квадрата ỳже нижней в cosa раз, где a - угол между горизонтальной плоскостью и радиусом сферы, проведенным из центра до пересечения с параллелью, или "широта" параллели. При нахождении второй параллели, откладываем на меридиане длину части первой параллели (меньшую, чем длина части экватора) и получаем еще один пояс криволинейных "квадратов". И далее "рекуррентно" продолжаем эту процедуру на нужное количество шагов (рис. 12г). Так как cos60°=1/2, ясно, что на широте 60° стороны "квадрата" должны быть уже вдвое меньше, чем стороны квадратов, примыкающих к "экватору". С помощью циркуля и линейки можно построить разрез такой сетки на куполе, имеющем изогнутую форму (и не обязательно куска поверхности шара).
Построить на сфере симметричный орнамент из подобных квантов, имеющих форму квадрата (вернее трапеции), можно следующим способом. "Экватор" делится на n равных частей (число на усмотрение создателя орнамента, обычно n=12, 16, 24). Через полученные на экваторе точки проводятся меридианы. По меридиану откладывается длина одной части, полученной на экваторе. На этом уровне проводится первая параллель ("экватор" – нулевая параллель). Получаем первый пояс из фигур, которые являются криволинейными "квадратами". Верхняя сторона квадрата ỳже нижней в cosa раз, где a - угол между горизонтальной плоскостью и радиусом сферы, проведенным из центра до пересечения с параллелью, или "широта" параллели. При нахождении второй параллели, откладываем на меридиане длину части первой параллели (меньшую, чем длина части экватора) и получаем еще один пояс криволинейных "квадратов". И далее "рекуррентно" продолжаем эту процедуру на нужное количество шагов (рис. 12г). Так как cos60°=1/2, ясно, что на широте 60° стороны "квадрата" должны быть уже вдвое меньше, чем стороны квадратов, примыкающих к "экватору". С помощью циркуля и линейки можно построить разрез такой сетки на куполе, имеющем изогнутую форму (и не обязательно куска поверхности шара).
 Проекция сферы на плоскость
Проекция сферы на плоскость
 . Эта проекция, она называется стереографической, хороша тем, что она не искажает углов и все окружности, лежащие на куполе, а не только параллели, переходят в окружности. Следовательно, проекции круглых розеток будут круглыми.
. Эта проекция, она называется стереографической, хороша тем, что она не искажает углов и все окружности, лежащие на куполе, а не только параллели, переходят в окружности. Следовательно, проекции круглых розеток будут круглыми.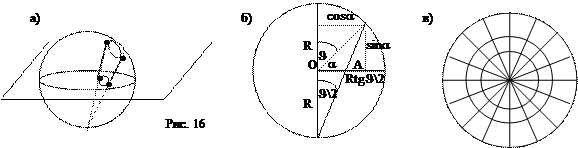
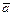 (3,-2) и
(3,-2) и  (1,2). Найдите координаты векторов 2
(1,2). Найдите координаты векторов 2 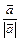 .
. .
. .
.

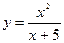 вся числовая прямая, из которой выколота точка х=-5, а для функции
вся числовая прямая, из которой выколота точка х=-5, а для функции 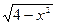 - отрезок -2£ х £2 и т.д.
- отрезок -2£ х £2 и т.д.



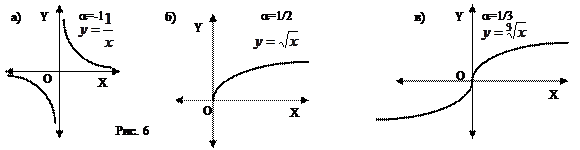
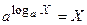 и формулу перехода от одного основания к другому: log a X=logbX×log a b=logbX:logb a. Его основные свойства: log ab =log a +log b,
и формулу перехода от одного основания к другому: log a X=logbX×log a b=logbX:logb a. Его основные свойства: log ab =log a +log b, 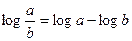 , log a m= m log a,
, log a m= m log a, 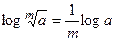

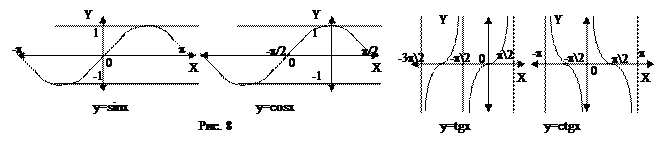
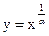 при разных значениях a, например, у=х2 и
при разных значениях a, например, у=х2 и 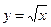 .
. - элементарные функции.
- элементарные функции.


