
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Двухстолпный и бесстолпный храмы
Особняком стоят 2 плана, в которых отношение полной длины к ширине "золотое", при этом один из них имеет только 2 столба (рис.12а), а второй не имеет столбов вообще (так называемый бесстолпный храм (рис. 12б). Без учета апсиды длина храма равна ширине, ширина алтарной части определяется с помощью диагонали половины этого квадрата.
План четырехстолпного храма План четырехстолпного храма, как правило, квадрат, или почти квадрат, центр купола не всегда проектируется в центр "квадрата", так как часто алтарный неф уже западного. С восточной стороны к квадрату присоединены апсиды. С учетом апсид в плане получается прямоугольник с отношением сторон, близким к 6:5, 5:4, 4:3, 21:20 или "нормальный" прямоугольник, с отношением сторон В качестве самого простого примера приведем схему плана собора Спаса-Преображения в Переяславле-Залесском (1152г.).
В интерьере длина храма без апсид равна его ширине, подкупольный квадрат расположен в центре этого квадрата, толщина столбов равна 1/4 части стороны подкупольного квадрата, лопатки выступают на 1/4 часть толщины столба (рис. 12в). Поперечные и продольные пропорции: 1:2:1:4:1:2:1. Отношение внутренней длины с учетом апсид к ширине равно5:4, наружные пропорции плана 6:5.
Глава 6 Размерение сооружений, имеющих "золотые" пропорции
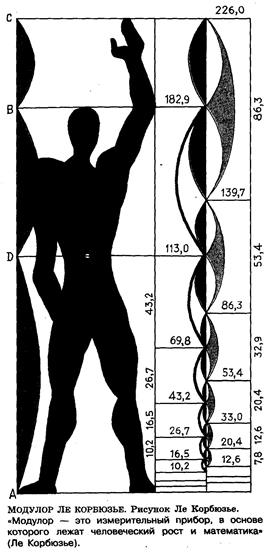
Модулер Корбюзье После окончания 2-й мировой войны полмира лежало в развалинах, и перед архитекторами встала новая для них задача разработки методик, позволяющих очень быстро создавать проекты достаточно качественных домов, состоящих из деталей, поставляемых заводами, т.е. имеющих стандартные размеры. Ле Корбюзье поставил себе целью придумать шкалу длин, которая позволяла бы легко задавать необходимые стандартные размеры, лучше всего в целых числах. Он посчитал, что в качестве такой шкалы хорошо взять геометрическую прогрессию, множитель которой равен "золотому" числу j. Скорее всего на эту мысль его навела универсальность "золотых" пропорций. Кроме множителя, значение членов геометрической прогрессии определяется еще и ее начальным значением. Этот параметр Корбюзье хотел подобрать так, чтобы прогрессия хорошо описывала человеческое тело, которое является для архитектора главным мерилом, и к тому же имеет "золотые" пропорции. Прогрессия должна была состоять из целых чисел и при этом задавать размеры в современных единицах измерения. Решение этой задачи было найдено с помощью последовательности Фибоначчи. Рост человека, равный 6 английским футам, выраженный в дюймах (6 футов=72 дюймам), совпал с одним из чисел Фибоначчи, поделенным на 2: 72=144:2 (английский фут равен 30,48см, он состоит из 12 дюймов, дюйм равен 2,54см, 6футов=183,5см). Следовательно, последовательность 72; 44,5; 27,5; 17; 10,5; 6,5; 4; 2,5; 1,5; 1… задает выраженные в дюймах высоту человека (72), расстояние от пола до пупка (44,5), от пупка до макушки и от колена до пупка (27,5), от пупка до основания шеи и от пола до колена (17), от основания шеи до макушки(10,5) и т.д. Эти параметры учитываются при разработке пропорций жилых помещений, мебели и т.д.
2j:1=1:Ф/2»1,236:1»1:0,809 - двойное золото,
Ф2/2:1»1,309:1, Сочетание рассмотренной нами шкалы и еще одной, парной ей, позволяет, не прибегая к вычислениям, описывать в целых числах все перечисленные пропорции. Значения второй шкалы строятся, начиная с высоты человека с поднятой вверх рукой - 226см. Это 89 дюймов, что также является числом из последовательности Фибоначчи. Таким образом, вторая шкала размеров в дюймах выглядит следующим образом: 89; 55; 34; 21; 13; 8; 5; 3; 2; 1; … Обе эти последовательности - рациональное приближение геометрической прогрессии с множителем j. Те, кто пользуется метрической шкалой, должны сделать пересчет значений из этих последовательностей, используя соотношение: 4дюйма»10см. Первую последовательность Корбюзье назвал красным рядом, вторую - голубым рядом.
Ф:1»1,618:1 - 89:55; 55:34; 34:21; 21:13; 13:8…, а также - 72:44,5; 44,5:27,5; 27,5:17,…. Чтобы получить отношение 2j:1 надо использовать оба ряда, например:
2j:1»1,236:1 - 89:72; 55:44,5; 34:27,5; 21:17. Для получения отношения Ф2/2:1»1,309:1 надо взять через один два члена последовательности (все равно красной или голубой) и больший поделить пополам, или член из красного ряда поделить на "соответствующий" член из голубого ряда, например: Ф2/2:1»1,309:1 - 17:13; 44,5:34; 27,5:21;…. Пропорцию "функция золота" 1,118:1 можно получить, используя линейную комбинацию 2-х соседних членов ряда Фибоначчи или разность соседних членов красного и голубого ряда: wn=un+1-un/2, wn:un» 89-55/2=61,5, 61,5:55» Если выписать значения wn=un+1-un/2 и vn=2wn=2un+1-un последовательно для n=1,2,…, то получим 2 ряда. Последовательность {vn} – это так называемый ряд Люка. Последовательность {wn} – его “красная” пара. Последовательность Люка строится так же, как последовательность Фибоначчи - значение n-ого члена последовательности вычисляется по формуле vn=vn-1+vn-2. Но начальными для нее являются не 1 и 1, как это имеет место для последовательности Фибоначчи (можно считать, что последовательность Фибоначчи начинается с этих 2-х чисел), а числа 1 и 3. Ряд Люка выглядит следующим образом: 1 3 4 7 11 18 29 47 76 123…. Покажем, что {vn} – ряд Люка. Действительно, v1=2u2-u1=2×1-1=1, v2=2u3-u2=2×2-1=3 vn=2u+1-un=2(un+un-1)-(un-1+un-2)=2un-un-1+2un-1-un-2=vn-1+vn-2 Отношение 2-х смежных членов zn/zn-1 любой последовательности {zn}, для которой выполняется: zn=zn-1+zn-2, с увеличением их номера в последовательности стремится к числу Ф. Таким образом, для получения рационального приближения для Ф можно использовать и соседние члены ряда Люка. Кроме того,
Действительно:
С помощью “красного” и “голубого” рядов Фибоначчи и Люка (Ф/2, Ф, Л/2, Л) можно построить " таблицу умножения " для произведений чисел Фибоначчи и Люка на множители, значение которых связано с Она, в свою очередь, позволяет составить “ таблицу рациональных отношений”, являющихся рациональными приближениями для "золотой" пропорции и ее производных.
Таблица умножения
Значение для производной Бурова 507:493»1.028 можно получить следующим способом. Такая пропорция получается, если выполнить деление отрезка в золотом отношении 3 раза. Выпишем получающиеся соотношения для отрезка длины 144 (для меньших длин точность не очень хорошая). 144=89+55=55+34+55 (первое деление), 34=21+13=13+8+13 (второе деление), 144=55+13+8+13+55, 8=5+3 (третье деление), 144=55+13+5+3+13+55, 73=55+13+5, 71=3+13+55. Аналогично пропорция 118:115 получается тройным делением в золотом отношении отрезка длины 233.
Таблица рациональных отношений
Таблицу (мы приводим далеко не все ее строки) можно использовать для построения отрезков, длины которых находятся в нужном пропорциональном отношении. Эти отрезки можно располагать на одной прямой (деление отрезка в заданной пропорции) или строить из них прямоугольники и треугольники (рис. 1). При составлении этой таблицы мы провели рассуждения на современном уровне, хотя построить такую таблицу можно с помощью самых простых рассуждений.
Обмеры архитектурных сооружений демонстрируют, что многие пропорциональные отношения, которые можно найти в размерах сооружений, имеются в этой таблице.
Меры древней Руси О том, как в древние времена происходил процесс размерения строящихся зданий, материальных свидетельств очень мало. Мало что известно и о мерах, которыми пользовались строители. Неизвестны нам и методы расчетов, применяемые архитекторами древности. На начальном этапе развития человеческого общества создавалась система мер, вырабатываемая практикой, и, несмотря на то, что в каждом государстве это была своя система, у всех этих систем много общего. Например, меры, использовавшиеся для измерения длин, как правило, были связаны с размерами человеческого тела. Таковы "локоть", "фут" (стопа), пядь, ладонь, палец. Но в разных местностях они имели разную длину. Афанасьев [1] приводит 2 фута, пришедших с византийскими мастерами, которые использовались на Руси, - примерно 29,6см (римский) и примерно 30,9см (греческий). Третья значащая цифра для разных сооружений может немного различаться. О Великой Печерской церкви в Киеве в летописи записано, что она имеет меру 20 "поясов Шимона" в ширину и 30 в длину. Обмеры по наружным стенам определили длину "пояса" примерно в 118см и это значение равно 4-м римским футам: 118см:4=29,5см. Исследованию древнерусских мер посвящено много работ русских архитекторов. Трудность исследований состоит в том, что единая система мер, не зависящая от района, появляется только в результате становления централизованного государства с развитыми торговыми и экономическими связями между районами и с сильной властью, осуществляющей единый контроль. И процесс введения единой меры непростой, так как он связан с ломкой предшествующей традиционной системы. Кроме того, разные меры могли применяться в торговле и строительстве, существовали меры народные, княжеские, церковные и т.д. В современной системе меры отличаются друг от друга в 10, 100, 1000 и т.д. раз. Расчеты ведутся также в десятичной системе, следовательно, одновременное существование метров и сантиметров, километров и метров не вызывают при расчетах никаких затруднений. Расчет легко производить практически для любого количества знаков, что уравнивает иррациональные величины с рациональными. Но такая система - плод многовековых усилий всего человечества. Пока она не была разработана, люди использовали в своей практике меры и методы, позволявшие вести расчеты в целых числах и простейших дробях. Изучение древних памятников и очень краткие описания, содержащиеся в дошедших до нас письменных источниках, позволили разным авторам создать реконструкцию древнерусских мер и методику работы с ними древних мастеров. Принято считать, что на Руси использовались сажени и их производные, получаемые с помощью деления сажени.
В Новгороде в культурном слое начала XIII века была найдена мерная трость ("мерило"), вернее, ее обломок. Обломок имеет длину около полуметра, он имеет прямоугольное сечение и на 3-х гранях из 4-х нанесены деления разной длины - длинные, длиной во всю грань, и короткие, делящие расстояние между длинными рисками на 10 равных частей. Расстояния между длинными рисками равны: на одной грани, мы будем называть ее первой буквой от слова “Тьмутаракань” Т, в среднем 59,3мм, на грани М (мерная) – 73,2мм, на грани Н (новгородская косая) – 83,5мм. Для этих значений выполняется: 73,2:59,3≈1,234≈2j 83,5:59,3≈1,408≈ 83,5:73,2≈1,141≈8/7 О том, каким единицам измерения соответствуют эти отрезки, можно только гадать, так как обломок очень короткий. Существуют разные реконструкции величины саженей, соответствующих "мерилу" (см., напр., [2, 3].
О том, что древние мастера при размерении одного и того же сооружения использовали не одну меру, а 2 или 3 разные меры одновременно, можно судить и по записям в летописях, когда в описании объекта используются сажени разных наименований. Приведем самый простой пример. В одной из рукописей, датируемой XVII веком, была сделана запись: "валили вал в ширину 25 сажен косых, а простых 40 сажен"(в этом примере отношение длины косой сажени к длине простой – 1,6) Имеются упоминания в летописях и о существовании деревянных "мерил". В "Сказании о Соломоне и Китоврасе" упоминаются "пруты" (во множественном числе), несколько деревянных мерил, изготовленных мудрым кентавром для создания "очертания" храма. Его "пруты" делились на 4 локтя. Как мы уже говорили, благодаря тесным связям мастеров древней Руси с культурой Византии русская метрология оказалась во многом связана с византийской, древнегреческой и древнеримской метрологическими системами. А на древнегреческую и древнеримскую в свою очередь оказали влияние метрологические системы Древнего Востока – Вавилона и древнего Египта. Можно сравнить новгородский мерный прут с египетским прутом. В Мемфисе при раскопках был найден мерный прут, на 4-х гранях которого нанесены риски, отмечающие размеры 4-х разных локтей – длины 520мм, 462мм, 443мм и 441мм (размеры в описании [5] указаны с точностью до миллиметра). Локоть длины 462мм соответствует футу длины 462мм:1,5=308мм (длина греческого фута), он состоит из 25 пальцев длины 18,48мм. Локоть длины 520мм связан с локтем длины 462мм соотношением: 520≈9/8∙462мм (462 9/8=519,75), т.е. разность длин этих локтей 520мм-462мм=58мм составляет 1/8 часть греческого локтя (462мм:8=57,75мм, 57,75∙9=519,75). С локтем длины 441мм греческий локоть находится в соотношении, позволяющем по диаметру окружности легко находить ее длину. Действительно: 462:441=1,0476…, 22:21=1,0476…, или 441=21/22∙463. Следовательно, если диаметр окружности равен локтю длины 441мм, то длина окружности L=441мм∙22/7=3∙462мм, т.е. 3-м локтям длины 462мм. Локоть длины 443мм соответствует римскому футу 443мм:1.5=295,3мм. Разность 520мм-443мм=77мм составляет 1/6 часть греческого локтя: 462мм:6=77мм. Локоть 443мм состоит из 24-х пальцев: 24∙1,848мм=443,52мм. Тем самым, мера длины 443мм оказывается связанной с мерой длины 462мм соотношением: 443мм=24/25∙462мм. В XVII-XVIIIвв. правительство в России начинает проводить политику упорядочивания мер, вводится аршин, равный 28 английским дюймам, состоящий из 16 вершков (см. след. главу), - единицы измерения, согласованные с английскими мерами длины, завоевавшие в дальнейшем прочные позиции. Глава 7 Измерение фигур В этой главе речь пойдет об измерении длин, площадей, объемов и углов. Для начала мы приведем список некоторых единиц измерения, которые были приняты во времена, когда еще не был осуществлен переход на единую метрическую систему. Наша система счета, денежная система и метрическая имеют основанием число 10. Тем самым, если цена указана для метра материи, то легко подсчитывается цена за кусок длиной в 1м 20см (цену за метр умножаем на 1,2 и получаем цену 1м 20см в рублях и копейках), если цена указана для 1кг крупы, то легко определяется, сколько стоят 630г и т.д. Измерительные системы прежних времен были менее удобными. Но все они подчинялись главному правилу – более мелкая единица измерения входила в более крупную единицу целое число раз. Только это было не 10, не 100, не 1000 раз - правило, которому подчинены мм, см, дм, м, км, или г, кг, центнер, тонна, рубли и копейки, а 2, 3, 4, 10, 12, 16 и т.д. раз. Это позволяло работать с третями и четвертями, а не с десятыми долями, как это принято в десятичной системе. Размеры основных единиц обеспечивали удобство измерений в повседневной практике. Измеряя длину, обычно пользовались единицами, тесно связанными со средними размерами человеческого тела. Напомним, что эталоны мер не отличались большой точностью и несоизмеримы с современными единицами.
Таблица перевода старых мер в современные единицы измерения Меры длины и площади (русские) 1 вершок=44,45мм=4,445см=7/4∙англ. дюймов (английский дюйм - 2,54см) 1 пядь=4 вершка≈17,78см (расстояние между большим и указательным пальцами) 1 аршин=16 вершков=71,12см=28 2,54см (28 англ. дюймов) 1 сажень=3 аршина=7 английских футов=84 дюйма≈213,36см (английский фут=30,48см) 1 верста=500саженей≈1,067км 1 миля (русская)=7верст≈7468м 1 десятина≈1,092га=2400 квадратных сажени – примерно 50´50 саженей, вернее 40´60 1 хозяйственная десятина=3600 кв. сажен (60´60), иногда 3200 кв. сажен (40´80) Меры веса (русские) 1 золотник=4,26г (по весу монетки) 1 лот=3 золотника≈12,79г 1 фунт=32 лота≈410г 1 пуд=40 фунтов≈16,38кг 1 берковец=10 пудов≈163,8кг Меры емкости (русские) 1 четверть (куль)≈210л (мешок, вмещающий соответствующее количество зерна) 1 бочка=40 ведер≈492л 1 ведро=10штофов≈12,3л 1 штоф≈1,23л 1 полуштоф≈0,6л 1 чарка=2шкалика≈0,12л 1 шкалик (косушка)≈0,06л Меры длины и площади (западные) 1 дюйм=10 линий=100 калибров=72 пункта≈2,54см 1 хенд=4 дюйма≈10,16см 1 фут=12 дюймов≈30,48см 1 ярд=3 фута≈91,44см 1фатом (морская сажень)≈1,83м 1 миля уставная (сухопутная)≈1,609км 1 морская миля=1' дуги меридиана≈1,852км 1 кабельтов=0,1 морской мили≈185,2м 1акр=70´70квадратных ярдов≈0,405га Меры веса (западные) 1 карат≈0,2г 1 унция≈28,35г 1 фунт=16 унций≈454г Меры объема жидкости (западные) 1 кварта=2 пинты≈1,1л 1 пинта=16 унций≈ 0,55л 1 галлон=4 кварты=8 пинт=128 унций≈4,5л 1 баррель (бочка)≈158,988л (нефтяной) Измерение температуры Существует три шкалы для измерения температуры. Все три были разработаны в первой половине ХVIII века. В настоящее время наибольшее распространение получила шкала Цельсия: температура таяния льда 0°С, кипения воды 100°С. Раньше в России для измерения температуры использовалась шкала Реомюра. По Реомюру принято, что температура кипения воды 80°Р, таяние льда при 0°Р. Шкала равномерная. В Америке всегда была принята шкала Фаренгейта: температура таяния льда 32°F, разница между температурой кипения воды и таяния льда 180°. Так что перевести в t°C приведенную в литературных источниках температуру можно по следующим формулам: t°C=10/8t°P, t°C=5/9(t°F-32)
Тригонометрические функции Тригонометрические функции угла a определяются с помощью тригонометрического круга радиуса r=1, а также из прямоугольного треугольника (для острых углов) (рис. 1).
Углы измеряются в градусах (0°£a£360°) (каждый градус состоит из 60' (минут), каждая минута из 60''(секунд)), или в радианах (0£a£2p). Полный угол состоит из 1296000''. При измерении угла в градусах, минутах, секундах возможное значение величины угла – рациональное число m/n, где n=1296000, а m – номер ближайшей секунды. Измерение углов в радианах - это фактически отождествление угла с дугой окружности единичного радиуса, на которую он опирается, т.е. величина угла может принимать любое значение, а не одно из 1296000 возможных. Угол в один радиан - это угол, который стягивается дугой, длина которой равна радиусу окружности. Длина окружности пропорциональна ее диаметру. Обозначение для этого коэффициента пропорциональности - p. Длина окружности единичного радиуса равна 2p. Тем самым, величина полного угла в радианах тоже равна 2p. Переход на радианы позволяет указывать величину угла с помощью линейной меры. Если прокатить колесо единичного радиуса по земле на один оборот, то след от колеса будет иметь длину 2p. Этот отрезок и будет соответствовать полному углу 2p радиан. Таким образом, можно сказать, что в градусах, минутах, секундах можно задавать "рациональные" значения углов, а в радианах - любые. Для практических целей обычно вполне хватает указания величины угла в градусах, минутах, секундах, это и удобнее, а в аналитических формулах в качестве аргумента используется значение угла, заданное в радианах. В качестве иллюстрации приведем построение графика синуса (рис. 2а). График строится на отрезке, длина которого равна длине окружности единичного радиуса, т.е. 2π. Для того, чтобы построить 12 опорных точек графика, окружность и горизонтальный отрезок длины 2π делим на 12 равных частей. Значение синуса угла равно длине полухорды. Откладываем по вертикали длины соответствующих полухорд.
На рисунке 3 показано, как из свойств равностороннего треугольника (рис 3а) и равнобедренного прямоугольного треугольника (рис. 3б) с помощью теоремы Пифагора получить значения тригонометрических функций для углов 0º, 30º, 45º, 60º, 90º.
Таблица значений тригонометрических функций для углов 0º, 30º,45º,60º90º
Пересчет градусной меры в радианную производится с помощью пропорции Формула показывает, что длина дуги пропорциональна радиусу. В силу этого можно сказать, что угол в один радиан стягивается дугой, длина которой равна радиусу окружности. Величина центрального угла не зависит от радиуса. p=3,1415926, 1радиан=57°17,5', arc1°=2π/360=0,01745, 1/p=0,31831
Решение треугольников Треугольник определен, если известны его стороны и углы (рис. 3в). Эти 6 параметров связаны друг с другом. Например, сумма углов треугольника, как известно, равна 180°. Следовательно, по 2-м известным углам однозначно определяется третий угол. Вообще говоря, для определения треугольника требуется задание не 6-ти, а всего 3-х параметров. Три стороны полностью определяют треугольник - по 3-м сторонам его можно построить с помощью циркуля и линейки (не забываем, что сумма любых 2-х сторон должна быть больше третьей стороны). Три угла определяют форму треугольника с точностью до подобия. Для того чтобы задать размер треугольника, необходимо задать хотя бы одну его сторону. Т.е. для того, чтобы задать треугольник, надо задать 3 стороны, или сторону и 2 угла, или две стороны и угол. Отсюда равносторонний и прямоугольный равнобедренный треугольник полностью определяются одной своей стороной - задавая длину стороны равностороннего треугольника, мы задаем значение 3-х параметров - длины всех его сторон, указывая, что прямоугольник прямоугольный, мы задаем его угол (90°), а условие "треугольник равнобедренный" означает, что если известна одна его сторона, то неизвестной является только одна, а не две стороны. Для того чтобы по заданным 3-м параметрам решить произвольный треугольник, надо воспользоваться теоремой синусов или теоремой косинусов, которые определяют соотношение между длинами сторон треугольника и его углами с помощью формул: a2=b2+c2-2bccosa - теорема косинусов (квадрат стороны D-ка равен сумме квадратов 2-х других сторон минус удвоенное произведение этих сторон на косинус угла между ними),
В этих формулах углы α, β и γ – противолежащие для сторон a, b и c, соответственно. В приложении приведена подробная таблица значений тригонометрических функций, необходимая при решении таких задач. Примеры 1. Даны три стороны D-ка. Найти его углы. Углы находим по теореме косинусов. 2. Даны сторона и два угла D-ка. Найти третий угол и остальные две стороны. Так как сумма углов D-ка равна 180°, то третий угол вычисляется через заданные углы (сумма заданных углов должна быть меньше 180°). Зная длину одной стороны D-ка и величину всех трех углов, длины остальных сторон находим по теореме синусов. Задача всегда имеет решение и притом единственное.
Площади плоских фигур а) Площадь прямоугольника S со сторонами a и b: S= ab. б) Площадь параллелограмма, имеющего основание а и высоту h: S=ah. в) Площадь трапеции, имеющей основания а1 и а2 и высоту h: S= 1/2 (a1+а2)h. г) Площадь треугольника, имеющего основание а и высоту h: S= 1/2 ah. д) Площадь круга радиуса r: S=pr2 (длина окружности радиуса r: L=2pr) е) Площадь кругового сектора, образованного центральным углом α круга радиуса r,
Египтяне вычисляли площадь круга по формуле: S=4(8/9)2R2=(16/9×R)2. Это приближение замечательно не только тем, что для p дает значение 3,16, но и тем, что представляет площадь круга в виде площади квадрата со стороной 16/9×R. Площадь такого квадрата лишь на 0,5% отличается от площади круга.
Многогранники Многогранником называется тело, граница которого состоит из кусков плоскостей. Простейшими примерами многогранников являются, например, куб и параллелепипед.
Правильные многогранники Если все грани многогранника - одинаковые правильные многоугольники, и все многогранные углы равны, то многогранник называется правильным. Уже Платону (IV в. до н.э.) было известно, что существует только 5 видов правильных многогранников.
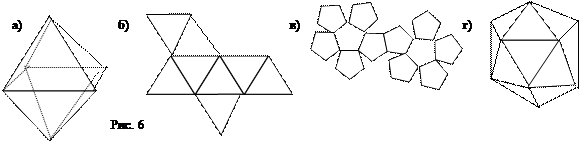
Из шести спичек можно составить четыре треугольника. Для этого нужно из трех спичек составить треугольник, лежащий в основании пирамиды, а три другие сделать ее боковыми ребрами. В результате получится правильный четырехгранник (тетраэдр) – первое из платоновых тел (рис. 5а). Его модель можно изготовить из бумаги, вырезав развертку, показанную на рисунке 5б. Второе платоново тело – это куб (рис. 5в). Если соединить центры граней куба, то получится третье платоново тело - правильный восьмигранник, так называемый октаэдр (рис 6а). Октаэдр можно составить из восьми равносторонних треугольников. Его развертка приведена на рис 6б. Если соединить средние точки боковых граней октаэдра, то получится куб (рис. 5г). Следующее платоново тело – правильный двенадцатигранник, имеет пятиугольные грани. Его модель можно получить из его развертки, приведенной на рис 6в. Последнее правильное тело – двадцатигранник (рис. 6г). Его развертка состоит из двадцати равносторонних треугольников.
Правильные пирамиды Пирамидой называется многогранник, у которого одна грань – основание пирамиды – произвольный многоугольник, а остальные – боковые грани – треугольники с общей вершиной S, называемой вершиной пирамиды. Перпендикуляр, опущенный из вершины пирамиды на основание, называется высотой пирамиды. Пирамида называется правильной, если ее основание – правильный многоугольник и высота падает в центр основания. В правильной пирамиде все боковые ребра равны, а все боковые грани равные равнобедренные треугольники. Высота боковой грани – это апофема правильной пирамиды. Правильная пирамида целиком определяется значением 2-х параметров. В качестве этой пары могут быть взяты длина ребра основания и высота, длина ребра основания и длина бокового ребра, длина ребра основания и апофема или угол наклона боковой грани. По 2-м заданным параметрам можно вычислить значения остальных параметров, используя только теорему Пифагора и тригонометрические таблицы.
Для того чтобы определить другие параметры пирамиды, воспользуемся тем, что мы знаем о равностороннем треугольнике (рис 7а) и равнобедренном прямоугольном треугольнике (рис. 7б). Высота пирамиды является катетом в прямоугольном треугольнике, гипотенуза которого равна 2 а, а второй катет равен половине диагонали квадрата со стороной 2 а, то есть равен
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1383; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.93.73 (0.194 с.) |
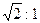 (1,414:1).
(1,414:1).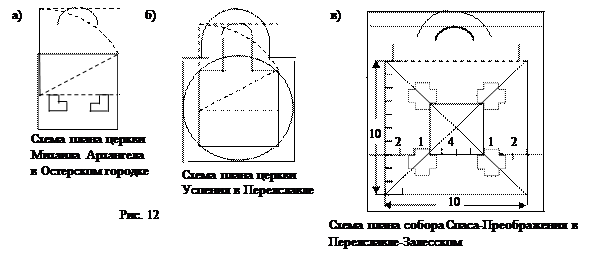
 Кроме "золотой" пропорции j:1=1:Ф»0,618:1»1:1,618, в архитектурных сооружениях широко применяются и другие пропорции, порождаемые диагональю полуквадрата. Их длины – рациональные выражения, в которые входит
Кроме "золотой" пропорции j:1=1:Ф»0,618:1»1:1,618, в архитектурных сооружениях широко применяются и другие пропорции, порождаемые диагональю полуквадрата. Их длины – рациональные выражения, в которые входит 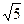 . Самые распространенные:
. Самые распространенные: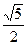 :1»1,118:1 - "функция золота",
:1»1,118:1 - "функция золота",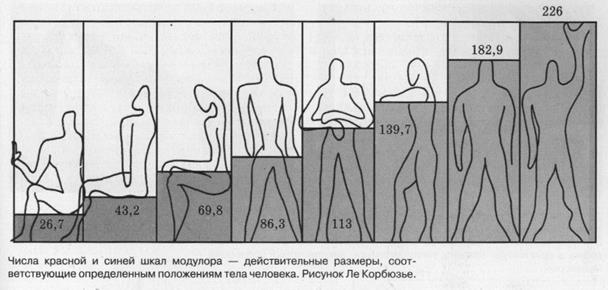 Для получения "золотой" пропорции годятся два соседних члена любой из шкал:
Для получения "золотой" пропорции годятся два соседних члена любой из шкал: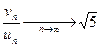 . Т.е. пара ряд Фибоначчи и ряд Люка дает решение в ближайших целых числах для произведения чисел Фибоначчи на
. Т.е. пара ряд Фибоначчи и ряд Люка дает решение в ближайших целых числах для произведения чисел Фибоначчи на 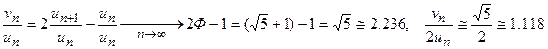
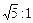 » 2.236:1
»1:0.447
» 2.236:1
»1:0.447




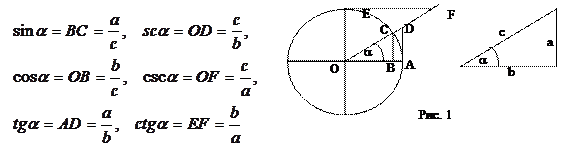

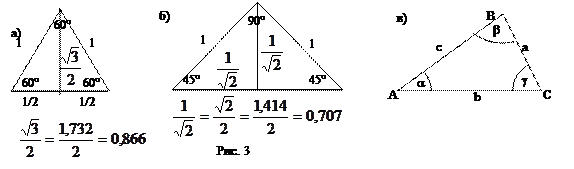
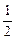
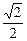
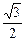
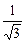
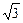
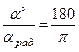 . Длина дуги l окружности радиуса r, опирающейся на центральный угол a, равна
. Длина дуги l окружности радиуса r, опирающейся на центральный угол a, равна 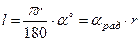 (рис. 2б).
(рис. 2б).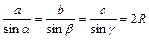 - теорема синусов (R - радиус описанной окружности)
- теорема синусов (R - радиус описанной окружности)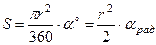
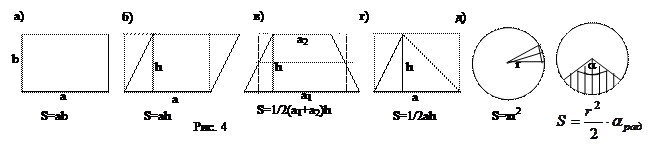

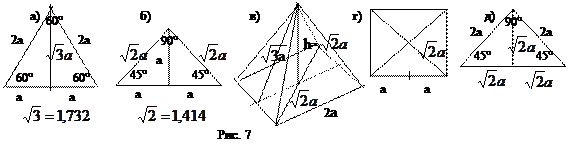 Рассмотрим правильную пирамиду, у которой в основании лежит квадрат со стороной 2 а, а боковые грани являются равносторонними треугольниками со стороной 2 а. У такой пирамиды все ребра равны между собой. Такая пирамида является половиной октаэдра (полуоктаэдр). Тот, кто хочет сделать макет такой пирамиды, может нарисовать квадрат, с каждой стороны квадрата пририсовать равносторонние треугольники, вырезать эту фигуру из бумаги и свести вместе вершины треугольников.
Рассмотрим правильную пирамиду, у которой в основании лежит квадрат со стороной 2 а, а боковые грани являются равносторонними треугольниками со стороной 2 а. У такой пирамиды все ребра равны между собой. Такая пирамида является половиной октаэдра (полуоктаэдр). Тот, кто хочет сделать макет такой пирамиды, может нарисовать квадрат, с каждой стороны квадрата пририсовать равносторонние треугольники, вырезать эту фигуру из бумаги и свести вместе вершины треугольников. (рис. 7в,г,д). По теореме Пифагора получаем, что
(рис. 7в,г,д). По теореме Пифагора получаем, что 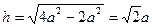 , и, следовательно, диагональное сечение такой пирамиды – равнобедренный прямоугольный треугольник и угол наклона бокового ребра равен 45°.
, и, следовательно, диагональное сечение такой пирамиды – равнобедренный прямоугольный треугольник и угол наклона бокового ребра равен 45°.


