
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интеграла от линии интегрирования
Формула Грина устанавливает связь между криволинейным интегралом по замкнутому контуру и двойным интегралом по области, ограниченной этим контуром. Теорема. Если функции
где замкнутый контур Теорема. Пусть функции
Эту функцию
где Начальную точку Пример 12.3. Вычислить Решение. Поскольку контур является замкнутым, применим формулу Грина. В нашем случае
Следовательно,
Пример 12.4. Найти функцию
Решение. Воспользуемся первой из формул (12.1), выбрав за начальную точку
Поскольку
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ 1. Найти 2. Показать, что выражение 3. Вычислить работу, производимую силой 4. Найти КОНТРОЛЬНЫЙ ТЕСТ ПО МОДУЛЮ №12
Модуль13. ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ
Скалярные и векторные поля. Геометрические характеристики полей Если в каждой точке Примерами скалярных полей являются: поле температуры Если в каждой точке
то говорят, что в области
Примерами векторных полей являются: поле скоростей
§ 2. Операторы теории поля: Оператор Гамильтона Важнейшими характеристиками скалярных и векторных полей являются градиент ( Определение. Градиентом дифференцируемого скалярного поля
Определение. Дивергенцией (или расходимостью) дифференци-руемого векторного поля
Определение. Ротором (или вихрем) дифференцируемого векторного поля
который с помощью символической записи удобно представить в виде векторного произведения
Операторы В качестве примеров использования указанных операторов приведем формулу связи напряженности
Здесь
В математической и особенно физической литературе наряду с вве-денными операторами широко используется символический вектор-ный дифференциальный оператор набла (оператор Гамильтона):
Правила работы с оператором Выразим операторы поля через оператор
Пример 13.1. Для вектора Решение.
Производная по направлению. Физический смысл градиента Пусть функция
Рис.13. 1
Из заданной точки Расстояние между точками
Тогда при переходе из точки
Определение. Если существует предел отношения
Теорема 1. Если функция
где С физической точки зрения производная по направлению характеризует скорость изменения функции в заданном направлении. Физический смысл градиента Вектор Пример 13.2. Вычислить производную функции Решение. Найдем частные производные функции
Вычислим длину и направляющие косинусы вектора
Следовательно, Производную по направлению найдем по формуле
Простейшие векторные поля К простейшим векторным полям относятся: соленоидальное, потенциальное и гармоническое. Определение. Векторное поле
Соленоидальное поле не имеет ни источников, ни стоков, его векторные линии замкнуты. Поскольку Определение. Векторное поле
Для потенциального векторного поля Определение. Векторное поле называется гармоническим, если во всех точках поля
т.е. поле является соленоидальным и потенциальным. Пример 13.3. Проверить, является ли векторное поле Решение. Векторное поле Найдем операторы:
Следовательно, поле является соленоидальным, но не является потенциальным. Таким образом, поле не является гармоническим.
Циркуляция векторного поля Рассмотрим непрерывное векторное поле Определение. Циркуляцией
В случае, когда векторное поле Если кривая Пример 13.4. Материальная точка массой
менной силы Решение. Запишем параметрические уравнения эллипса
Циркуляция вектора
где Примеры циркуляций векторных полей 1. Циркуляция вектора напряженности
2. Циркуляция вектора напряженности
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 316; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.248.149 (0.066 с.) |
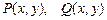 непрерывны вместе со своими частными производными в некоторой замкнутой области
непрерывны вместе со своими частными производными в некоторой замкнутой области  с границей
с границей 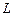 , то справедлива следующая формула Грина:
, то справедлива следующая формула Грина:
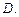 Для того, чтобы криволинейный интеграл
Для того, чтобы криволинейный интеграл  не зависел от пути интегрирования, целиком лежащем в области
не зависел от пути интегрирования, целиком лежащем в области  . Если выполняется это условие, то выражение
. Если выполняется это условие, то выражение 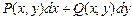 представляет собой полный дифференциал некоторой функции
представляет собой полный дифференциал некоторой функции 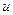 , т.е.
, т.е.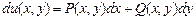 .
.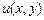 можно найти по одной из следующих двух формул
можно найти по одной из следующих двух формул (12.1)
(12.1) – произвольная постоянная.
– произвольная постоянная.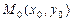 следует выбирать так, чтобы подынтегральные функции
следует выбирать так, чтобы подынтегральные функции  и
и 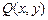 были определены в этой точке (удобно выбирать одну из точек
были определены в этой точке (удобно выбирать одну из точек 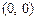 , (0, 1), (1, 1) и т.д.).
, (0, 1), (1, 1) и т.д.).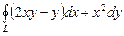 , где
, где  с вершинами в точках А (–1, 0), В (0, 2), С (0, 1) (рис. 12.2).
с вершинами в точках А (–1, 0), В (0, 2), С (0, 1) (рис. 12.2). 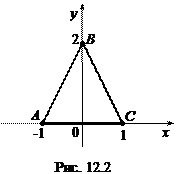
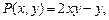
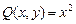 ,
,  ,
, 
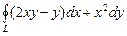 =
= 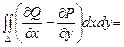
 .
.
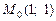 . Такой выбор вызван тем, что при
. Такой выбор вызван тем, что при 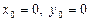 функции
функции 

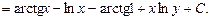
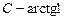 также является постоянной, то окончательный ответ можно записать в виде
также является постоянной, то окончательный ответ можно записать в виде 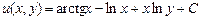 .
.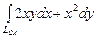 , если
, если  – дуга кривой
– дуга кривой 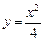 , заключенная между точками
, заключенная между точками  и
и 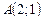 .
.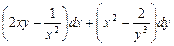 является полным дифференциалом функции
является полным дифференциалом функции  . Найти функцию
. Найти функцию 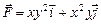 вдоль отрезка прямой от точки
вдоль отрезка прямой от точки  до точки
до точки  .
.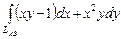 , где
, где 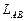 - дуга эллипса
- дуга эллипса 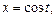
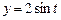 от точки
от точки 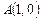 до точки
до точки 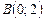 .
.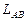 в плоскости
в плоскости  задана уравнением
задана уравнением 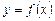 ,
, 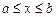 , то
, то 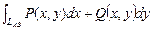 находится по формуле:
а)
находится по формуле:
а) 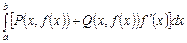 ; б)
; б) 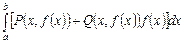 ;
в)
;
в)  ;г)
;г) 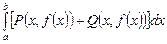 .
.
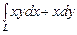 от т.
от т.  до т.
до т. 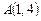 , если
, если  .
.
 не зависит от пути интегрирования, если
а)
не зависит от пути интегрирования, если
а)  ; б)
; б) 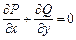 ; в)
; в) 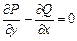 ; г)
; г) 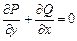 .
.
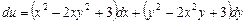 , то функция
, то функция  находится по формуле
а)
находится по формуле
а) 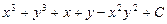 ; б)
; б) 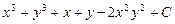 ;
в)
;
в)  ; г)
; г) 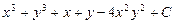 .
.
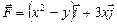 вдоль дуги кривой
вдоль дуги кривой 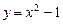 от точки
от точки 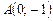 до точки
до точки  , равна
а)1; б) 6; в)3; г)0.
, равна
а)1; б) 6; в)3; г)0.
 , если
, если 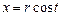 ,
, 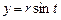 , пробегаемая против хода часовой стрелки.
а)0; б)
, пробегаемая против хода часовой стрелки.
а)0; б) 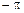 ; в)
; в)  ; г)
; г) 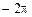 .
.
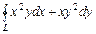 преобразуется в интеграл
а)
преобразуется в интеграл
а)  ;б)
;б)  ;в)
;в)  ;г)
;г) 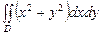 .
.
 некоторой области
некоторой области  пространства (или плоскости) определена скалярная функция
пространства (или плоскости) определена скалярная функция 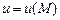 , то говорят, что в области
, то говорят, что в области  .
. внутри тела, поле потенциала
внутри тела, поле потенциала  электрического заряда, поле плотности
электрического заряда, поле плотности 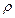 тела и т.д.
тела и т.д.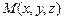 некоторой области
некоторой области 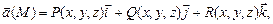
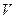 задано векторное поле
задано векторное поле .
.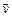 теку-щей жидкости, поле электрической напряженности
теку-щей жидкости, поле электрической напряженности 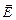 , поле магнитной напряженности
, поле магнитной напряженности  и т.д.
и т.д.
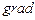 ) скалярного поля, дивергенция
) скалярного поля, дивергенция  и ротор
и ротор 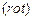 векторного поля.
векторного поля. называется вектор
называется вектор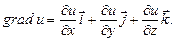
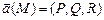 называется скаляр
называется скаляр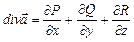 .
.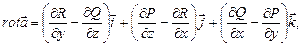
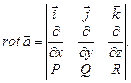
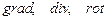 называются основными операторами теории поля.
называются основными операторами теории поля.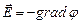 и систему уравнений Максвелла для стационарного электромагнитного поля:
и систему уравнений Максвелла для стационарного электромагнитного поля: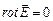 .
.
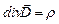 .
.
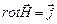 .
.
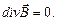
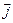 – вектор плотности электрического тока,
– вектор плотности электрического тока,  – вектор электрического смещения,
– вектор электрического смещения,  – вектор магнитной индукции,
– вектор магнитной индукции, 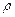 – плотность электрического заряда.
– плотность электрического заряда.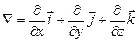 .
.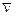 такие же, как и с обычными векторами.
такие же, как и с обычными векторами. , скалярное и векторное произведения вектора
, скалярное и векторное произведения вектора 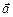 , получим формулы
, получим формулы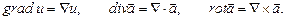
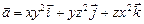 найти
найти  и
и 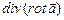 .
. ,
,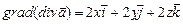 ,
,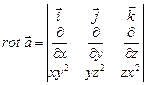
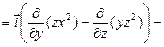
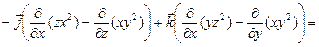
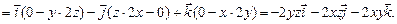
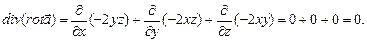
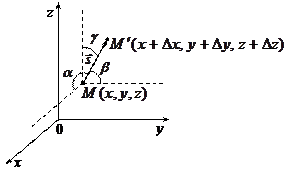

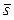 . На луче, задаваемом вектором
. На луче, задаваемом вектором 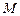 , отметим точку
, отметим точку  (рис.13.1).
(рис.13.1).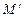 обозначим через
обозначим через 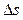 . Поэтому
. Поэтому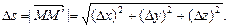
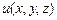 получит приращение
получит приращение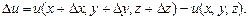
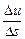 , когда
, когда 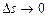 , то он называется производной функции
, то он называется производной функции 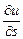 , т.е. по определению
, т.е. по определению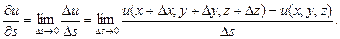
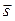 существует в каждой точке области и равна
существует в каждой точке области и равна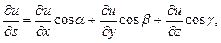
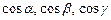 – направляющие косинусы вектора
– направляющие косинусы вектора 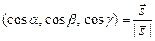 .
. к каждой точке
к каждой точке 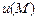 ортогонален поверхности уровня этого поля и указывает направление наиболее быстрого роста функции
ортогонален поверхности уровня этого поля и указывает направление наиболее быстрого роста функции 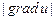 дает скорость этого роста.
дает скорость этого роста.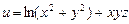 по направлению вектора
по направлению вектора 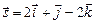 в точке
в точке 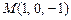 .
.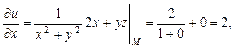
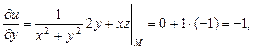
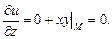
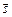 :
:
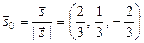 .
.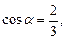
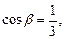

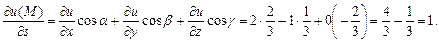
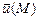 называется соленоидальным или трубчатым, если во всех точках поля
называется соленоидальным или трубчатым, если во всех точках поля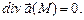
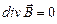 , то поле вектора магнитной индукции является соленоидальным.
, то поле вектора магнитной индукции является соленоидальным. называется потенциальным или безвихревым, если во всех точках поля
называется потенциальным или безвихревым, если во всех точках поля
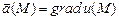 .
.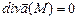 и
и 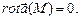
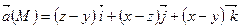 гармоническим.
гармоническим.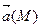 называется гармоническим, если оно является соленоидальным и потенциальным, то есть в каждой точке М поля выполняются равенства
называется гармоническим, если оно является соленоидальным и потенциальным, то есть в каждой точке М поля выполняются равенства 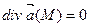 и
и  .
. ,
,

 .
.
 определенное в каждой точке гладкой замкнутой кривой
определенное в каждой точке гладкой замкнутой кривой 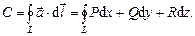
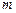 движется по эллипсу
движется по эллипсу 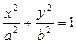 в положительном направлении под действием пере-
в положительном направлении под действием пере- , где
, где 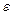 – угловое ускорение. Вычислить циркуляцию вектора
– угловое ускорение. Вычислить циркуляцию вектора  вдоль контура
вдоль контура 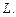

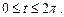
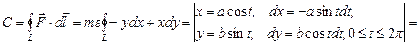
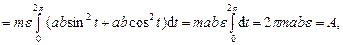
 – работа силы
– работа силы 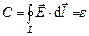 .
.



