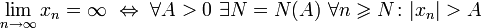Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос30. Предикат. Множество истинности предиката. Кванторы общности существования. Виды формулировок теорем (прямая и обратная теоремы, теорема о необходимых и достаточных условиях).
Предика́т (лат. praedicatum — заявленное, упомянутое, сказанное) — любое математическое высказывание, в котором есть, по меньшей мере, одна переменная. Предикат является основным объектом изучения логики первого порядка.Предикат – выражение с логическими переменными, имеющие смысл при любых допустимых значениях этих пременных.Выражения: х > 5, x > y – предикаты.Предика́т (n -местный, или n -арный) — это функция с множеством значений {0,1} (или «ложь» и «истина»), определённая на множестве
Предикат называют выполнимым, если хотя бы на одном наборе аргументов он принимает значение 1. Так как предикаты принимают только два значения, то к ним применимы все операции булевой алгебры, например: отрицание, импликация, конъюнкция, дизъюнкция и т. дКва́нтор — общее название для логических операций, ограничивающих область истинности какого-либо предиката. Чаще всего поминают: Квантор всеобщности (обозначение: Квантор существования (обозначение: Примеры Обозначим P (x) предикат «x делится на 5». Используя квантор общности, можно формально записать следующие высказывания (конечно, ложные): любое натуральное число кратно 5; каждое натуральное число кратно 5; все натуральные числа кратны 5; следующим образом: Следующие (уже истинные) высказывания используют квантор существования: существуют натуральные числа, кратные 5; найдётся натуральное число, кратное 5;
хотя бы одно натуральное число кратно 5. Их формальная запись: Пусть на множестве Х простых чисел задан предикат Р(х): «Простое число х — нечётно». Подставим перед этим предикатом слово «любое». Получим ложное высказывание «любое простое число х нечётно» (это высказывание ложно, так как 2 — простое чётное число). Подставив перед данным предикатом Р(х) слово «существует», получим истинное выказывание «Существует простое число х, являющееся нечётным» (например, х=3). Таким образом, превратить предикат в высказывание можно, поставив перед предикатом слова: «все», «существует», и др., называемые в логике кванторами. Кванторы в математической логике Высказывание («При всех значениях (x) утверждение верно»). Высказывание («Существует (x) при котором утверждение верно»).
Вопрос31 Граф и его элементы. Основные понятия. Инцидентность, кратность, петля, смежность. Типы графов. Маршрут в графе и его длина. Классификация маршрутов. Матрицы смежности ориентированного и неориентированного графов. Граф — это совокупность непустого множества вершин и множества пар вершин.Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах. Путём (или цепью) в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром.Ориентированным путём в орграфе называют конечную последовательность вершин vi
Путь (или цикл) называют простым, если ребра в нём не повторяются; элементарным, если он простой и вершины в нём не повторяются. Несложно видеть, что: Всякий путь, соединяющий две вершины, содержит элементарный путь, соединяющий те же две вершины. Всякий простой неэлементарный путь содержит элементарный цикл. Всякий простой цикл, проходящий через некоторую вершину (или ребро), содержит элементарный (под-)цикл, проходящий через ту же вершину (или ребро). Петля — элементарный цикл.Граф или неориентированный граф G — это упорядоченная пара G: = (V, E), для которой выполнены следующие условия: V это непустое множество вершин или узлов, E это множество пар (в случае неориентированного графа — неупорядоченных) вершин, называемых рёбрами. V (а значит и E, иначе оно было бы мультимножеством) обычно считаются конечными множествами. Многие хорошие результаты, полученные для конечных графов, неверны (или каким-либо образом отличаются) для бесконечных графов. Это происходит потому, что ряд соображений становится ложным в случае бесконечных множеств.Вершины и рёбра графа называются также элементами графа, число вершин в графе | V | — порядком, число рёбер | E | — размером графа. Вершины u и v называются концевыми вершинами (или просто концами) ребра e = { u, v }. Ребро, в свою очередь, соединяет эти вершины. Две концевые вершины одного и того же ребра называются соседними.Два ребра называются смежными, если они имеют общую концевую вершину.Два ребра называются кратными, если множества их концевых вершин совпадают.Ребро называется петлёй, если его концы совпадают, то есть e = { v, v }.Степенью deg V вершины V называют количество инцидентных ей рёбер(при этом петли считают дважды).Вершина называется изолированной, если она не является концом ни для одного ребра; висячей (или листом), если она является концом ровно одного ребра.Ориентированный граф (сокращённо орграф) G — это упорядоченная пара G: = (V, A), для которой выполнены следующие условия: V это непустое множество вершин или узлов, A это множество (упорядоченных) пар различных вершин, называемых дугами или ориентированными рёбрами. Дуга — это упорядоченная пара вершин (v, w), где вершину v называют началом, а w — концом дуги. Можно сказать, что дуга Ориентированный и неориентированный графы являются частными случаями смешанного. Изоморфные графы(?)Граф G называется изоморфным графу H, если существует биекция f из множества вершин графа G в множество вершин графа H, обладающая следующим свойством: если в графе G есть ребро из вершины A в вершину B, то в графе H должно быть ребро из вершины f (A) в вершину f (B) и наоборот — если в графе H есть ребро из вершины A в вершину B, то в графе G должно быть ребро из вершины f − 1(A) в вершину f − 1(B). В случае ориентированного графа эта биекция также должна сохранять ориентацию ребра. В случае взвешенного графа биекция также должна сохранять вес ребра. Матрица смежности графа G с конечным числом вершин n (пронумерованных числами от 1 до n) — это квадратная матрица A размера n, в которой значение элемента aij равно числу рёбер из i -й вершины графа в j -ю вершину.Иногда, особенно в случае неориентированного графа, петля (ребро из i -й вершины в саму себя) считается за два ребра, то есть значение диагонального элемента aii в этом случае равно удвоенному числу петель вокруг i -й вершины.
Матрица смежности простого графа (не содержащего петель и кратных ребер) является бинарной матрицей и содержит нули на главной диагонали.
Вопрос32 Функция. Способы задания. Классификация функций. Основные элементарные функции и их графики. Композиция функций. Элементарные функции. Функция — понятие, отражающее связь между элементами множеств. Функция это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений). Способы задания функции Аналитический способ Для задания функции пользуются выражением:
Однако, во многих разделах математики, можно обозначать через f(x) как саму функцию, так и аналитическое выражение, ее задающее Графический Пропорциональные величины. Если переменные y и x прямо пропорциональны, то функциональная зависимость между ними выражается уравнением: y = k x, где k - постоянная величина (коэффициент пропорциональности). График прямой пропорциональности – прямая линия, проходящая через начало координат и образующая с осью X угол Линейная функция. Если переменные y и x связаны уравнением 1-ой степени: A x + B y = C, где по крайней мере одно из чисел A или B не равно нулю, то графиком этой функциональной зависимости является прямая линия. Если C = 0, то она проходит через начало координат, в противном случае - нет. Графики линейных функций для различных комбинаций A, B, C
Обратная пропорциональность. Если переменные y и x обратно пропорциональны, то функциональная зависимость между ними выражается уравнением: y = k / x, где k - постоянная величина.
Основные характеристики и свойства гиперболы: - область определения функции: x - функция монотонная (убывающая) при x < 0и при x > 0, но не монотонная в целом из-за точки разрыва x = 0); - функция неограниченная, разрывная в точке x = 0, нечётная, непериодическая; - нулей функция не имеет.
- область определения функции: - значений: R - функция в целом не монотонна, но справа или слева от вершины ведёт себя, как монотонная; - функция неограниченная, всюду непрерывная, чётная при b = c = 0, и непериодическая; - при D < 0 не имеет нулей.
Основные характеристики и свойства показательной функции: - область определения функции: - область значений: y > 0; - функция монотонна: возрастает при a > 1 и убывает при 0 < a < 1; - функция неограниченная, всюду непрерывная, непериодическая; - нулей функция не имеет.
Логарифмическая функция. Функция y = log a x, где a – постоянное положительное число,не равное 1, называется логарифмической. Эта функция является обратной к показательной функции; её график) может быть получен поворотом графика показательной функции вокруг биссектрисы 1-го координатного угла.
- область определения функции: x > 0,а область значений: - - это монотонная функция: она возрастает при a > 1 и убывает при 0 < a < 1; - функция неограниченная, всюду непрерывная, непериодическая; - у функции есть один ноль: x = 1.
Тригонометрические функции. При построении тригонометрических функций мы используем радианную меру измерения углов.Тогда функция y = sin x представляется. Эта кривая называется синусоидой.
График функции y = cos x представлен; это также синусоида, полученная в результате перемещения графика y = sin x вдоль оси Х влево на
характеристики и свойства этих функций: - область определения: - - эти функции периодические: их период 2 - функции ограниченные (| y | ведут себя, как монотонные функции;
Композиция функций Если даны два отображения
Сквозное отображение
Таким образом, Вопрос33 Взаимно-однозначное соответствие между множествами. Обратное правило и обратная функция. Графики взаимно обратных функций. Определения, свойства и графики гиперболических функций. Мощностью конечного множества (множества, содержащего конечное число элементов) называется количество его элементов. Мощность множества A обозначается m (A). Пример 1 Определите мощность множества A = {1, 3, 5, 7, 9} нечётных чисел. Показать решение Простым пересчётом элементов убеждаемся, что нечётных чисел всего 5, и потому m (A) = 5. Ответ. 5. Ясно, что понятие мощности конечных множеств позволяет сравнивать их по количеству элементов. Так, если A = {1, 3, 5, 7, 9}, а B = {2, 4, 6, 8}, то m (A) = 5, а m (B) = 4 и потому m (A) > m (B). Однако если мы имеем дело с бесконечными множествами, то пересчитать элементы множества уже не удастся. Но иногда можно, как говорят, установить взаимно однозначное соответствие между двумя бесконечными множествами. Говорят, что между множествами A и B установлено взаимно однозначное соответствие, если из элементов этих множеств можно составить пары (a, b), причем каждый элемент из A и каждый элемент из B входят в одну и только одну пару. Множества, между которыми установлено взаимно однозначное соответствие, содержат одинаковое количество элементов. Множества A и B называют равномощными, если между их элементами можно установить взаимно однозначное соответствие (ещё говорят: можно установить взаимно однозначное отображение множеств). Мощность множества натуральных чисел обозначается א. Алеф א – первая буква еврейского алфавита, так обозначается наименьшая возможная для бесконечных множеств мощность. Множества, равномощные множеству натуральных чисел, называются счётными множествами. Пример 2 Множество натуральных чисел равномощно множеству нечётных чисел, так как между ними можно установить взаимно однозначное соответствие, например, по следующему правилу: 1 2 3... n... ↕ ↕ ↕ ↕ 1 3 5... 2 n – 1... Так как множество нечётных чисел является подмножеством натуральных чисел, то этот пример показывает, что бесконечное множество может быть равномощно своему подмножеству. Пример 3 Множество положительных рациональных чисел счётно. Действительно, если представить каждое рациональное число в виде несократимой дроби и записать его в следующую таблицу, а затем пронумеровать, как указано на рисунке, то окажется, что множество рациональных положительных чисел действительно счётно.
Пример 4 Любой отрезок [ a; b ] равномощен отрезку [0; 1]. Взаимно однозначное соответствие между ними устанавливает формула y = (b − a) · x + a, где x Пример 5 Множества A Существуют и другие бесконечные множества, мощность которых больше, чем мощность счётных множеств. Так, множество всех точек отрезка [0; 1] не равномощно множеству натуральных чисел Как было показано в примере 4, множество всех точек отрезка [0; 1] равномощно множеству точек отрезка любой длины. Легко показать равномощность множеств отрезка [ a; b ] и интервала (a; b), а также отрезка [ a; b ] и луча (a; +∞). Наконец, можно доказать равномощность множеств всех точек отрезка и квадрата. Мощность множества всех действительных чисел (или, что то же, множества всех точек числовой оси) обозначается символом c («континуум»). Поскольку множество всех действительных чисел несчётно, то א < c. Континуум – не самая большая из бесконечных мощностей. Так, мощность множества всех подмножеств точек числовой оси больше, чем мощность самого множества всех точек оси. Она обозначается 2 c и называется гиперконтинуумом.
Обратная функция. Теорема о существовании и непрерывности обратной функции. f−1(f(x))=f(f−1(x))=x.
Монотонные функции и их свойства. Теорема 2. Если функция y=f(x) строго возрастает (убывает) и непрерывна на промежутке I, то существует обратная функция x=f−1(y), которая определена на промежутке Ef=f(I) и является на Е, строго возрастающей (убывающей) и непрерывной. Покажем, что f−1 строго возрастает на Е. Пусть y1 и y2-- две произвольные точки из Е, такие, что y1<y2 и прообразами этих точек будут точки x1и x2. f−1(y1)=x1, и f−1(y2)=x2. Поскольку f - строго возрастающая функция, то неравенство y1=f(x1)<f(x2)=y2 возможно тогда и только тогда когда x1<x2 или тоже самое, когда f−1(y1)<f−1(y2). В силу произвольности y1 и y2 ∈E делаем вывод, что функция f−1 - строго возрастает на множестве Е. Что и требовалось доказать. 1. Гиперболическими синусом, косинусом, тангенсом и котангенсом называются функции:
ch(x± y)=chx · chy ± shx · shy, (1) sh(x± y)=shx · chy± chx · shy, (2) ch2x–sh2x=1, (3) ch2x=ch2x+sh2x, (4) sh2x=2shx · chx. (5) Тождества (2) и (5) аналогичны соответствующим формулам тригонометрии, а формулы (1), (3) и (4) отличаются от тригонометрических только знаком. Доказываются тождества (1) – (5) непосредственной проверкой. Более подробно о тождествах для гиперболических функций изложено в разделе III.
2. Рассмотрим уравнение гиперболы: Его можно записать в параметрическом виде, используя гиперболические функции (этим и объясняется их название). Обозначим y= b·sht, тогда х2 / а2=1+sh2t =ch2t. Откуда x=± a·cht.Таким образом мы приходим к следующим параметрическим уравнениям гиперболы:
x= ± a ·cht,у= в ·sht, –
Рис. 1. Знак ''+'' в верхней формуле (6) соответствует правой ветви гиперболы, а знак ''– '' - левой (см. рис. 1). Вершинам гиперболы А(– а; 0) и В(а; 0) соответствует значение параметра t=0. Для сравнения можно привести параметрические уравнения эллипса, использующие тригонометрические функции:x=а·cost,
2) (chx)'=shx (показывается аналогично).
4) Здесь так же прослеживается определенная аналогия с тригонометрическими функциями. Полная таблица производных всех гиперболических функций приведена в разделе IV. 6. Нетрудно вычислить вторые производные основных гиперболических функций: 1)
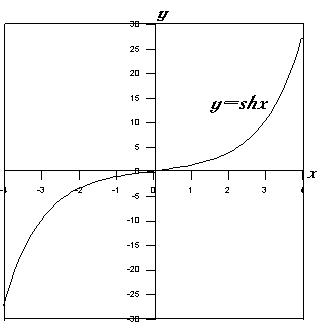
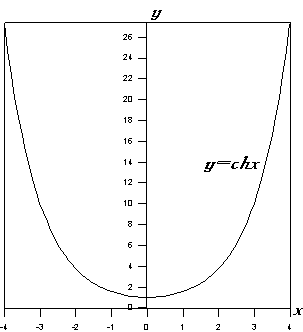
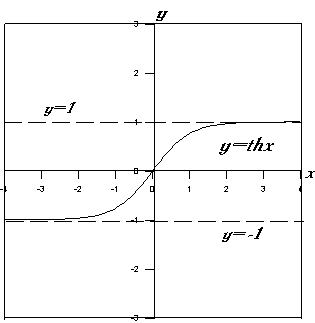
3) 7. Используя результаты п. 1-6, строим графики основных гиперболических функций:
Вопрос34. Числовая последовательность. Предел числовой последовательности (конечный и бесконечный). Геометрическая иллюстрация. Теорема о сходимости монотонной и ограниченной последовательности. Последовательность — это пздц (набор) элементов некоторого множества: для каждого натурального числа можно указать элемент данного множества; это число является номером элемента и обозначает позицию данного элемента в последовательности; для любого элемента (члена) последовательности можно указать следующий за ним элемент последовательности. Таким образом, последовательность оказывается результатом последовательного выбора элементов заданного множества. И, если любой набор элементов является конечным, и говорят о выборке конечного объёма, то последовательность оказывается выборкой бесконечного объёма. Последовательность по своей природе — отображение, поэтому его не следует смешивать с множеством, которое «пробегает» последовательность. В математике рассматривается множество различных последовательностей: числовые последовательности; временные ряды как числовой, так и не числовой природы; последовательности элементов метрического пространства последовательности элементов функционального пространства последовательности состояний систем управления и автоматов. Целью изучения всевозможных последовательностей является поиск закономерностей, прогноз будущих состояний и генерация последовательностей. Определение Пусть задано некоторое множество X элементов произвольной природы. Всякое отображение Образ натурального числа n, а именно, элемент xn = f (n), называется n -ым членом или элементом последовательности, а порядковый номер члена последовательности — её индексом. Связанные определения Подмножество Если взять возрастающую последовательность натуральных чисел, то её можно рассматривать как последовательность индексов некоторой последовательности: если взять элементы исходной последовательности с соответствующими индексами (взятыми из возрастающей последовательности натуральных чисел), то можно снова получить последовательность, которая называется подпоследовательностью заданной последовательности.
Предел числовой последовательности — предел последовательности элементов числового пространства. Числовое пространство — это метрическое пространство, расстояние в котором определяется как модуль разности между элементами. Поэтому, предел числовой последовательности — это такое число, что для всякой сколь угодно малой величины существует номер, начиная с которого уклонение членов последовательности от данной точки становится меньше заранее заданной величины. Понятие предела последовательности вещественных чисел формулируется совсем просто, а в случае комплексных чисел существование предела последовательности равносильно существованию пределов соответствующих последовательностей вещественных и мнимых частей комплексных чисел. Предел (числовой последовательности) — одно из основных понятий математического анализа. Каждое вещественное число может быть представлено как предел последовательности приближений к нужному значению. Система счисления предоставляет такую последовательность уточнений. Целые и рациональные числа описываются периодическими последовательностями приближений, в то время как иррациональные числа описываются непериодическими последовательностями приближений. [1] В численных методах, где используется представление чисел с конечным числом знаков, особую роль играет выбор системы приближений. Критерием качества системы приближений является скорость сходимости. В этом отношении, оказываются эффективными представления чисел в виде цепных дробей. Определение Число
В случае, если у числовой последовательности существует предел в виде вещественного числа
Кроме того, если все элементы неограниченной последовательности, начиная с некоторого номера, имеют положительный знак, то говорят, что предел такой последовательности равен плюс бесконечности.
Если же элементы неограниченной последовательности, начиная с некоторого номера, имеют отрицательный знак, то говорят, что предел такой последовательности равен минус бесконечности.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1544; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.61.16 (0.136 с.) |
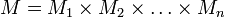 . Таким образом, каждый набор элементов множества M характеризуется либо как «истинный», либо как «ложный».Предикат можно связать с математическим отношением: если n -ка принадлежит отношению, то предикат будет возвращать на ней 1. В частности, одноместный предикат определяет отношение принадлежности некоторому множеству.Предикат — один из элементов логики первого и высших порядков. Начиная с логики второго порядка, в формулах можно ставить кванторы по предикатам.Предикат называют тождественно-истинным и пишут:
. Таким образом, каждый набор элементов множества M характеризуется либо как «истинный», либо как «ложный».Предикат можно связать с математическим отношением: если n -ка принадлежит отношению, то предикат будет возвращать на ней 1. В частности, одноместный предикат определяет отношение принадлежности некоторому множеству.Предикат — один из элементов логики первого и высших порядков. Начиная с логики второго порядка, в формулах можно ставить кванторы по предикатам.Предикат называют тождественно-истинным и пишут: если на любом наборе аргументов он принимает значение 1.Предикат называют тождественно-ложным и пишут:
если на любом наборе аргументов он принимает значение 1.Предикат называют тождественно-ложным и пишут: если на любом наборе аргументов он принимает значение 0.
если на любом наборе аргументов он принимает значение 0. , читается: «для всех…», «для каждого…» или «каждый…», «любой…», «для любого…»).
, читается: «для всех…», «для каждого…» или «каждый…», «любой…», «для любого…»).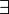 , читается: «существует…» или «найдётся…»).
, читается: «существует…» или «найдётся…»). .
.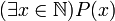 .Введение в понятие
.Введение в понятие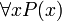 означает, что область значений переменной x включена в область истинности предиката P (x).
означает, что область значений переменной x включена в область истинности предиката P (x).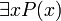 означает, что область истинности предиката P (x) непуста.
означает, что область истинности предиката P (x) непуста.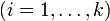 , для которой все пары (vi, vi + 1)
, для которой все пары (vi, vi + 1) 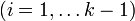 являются (ориентированными) рёбрами.Циклом называют путь, в котором первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют число составляющих его рёбер. Заметим, что если вершины u и v являются концами некоторого ребра, то согласно данному определению, последовательность (u, v, u) является циклом. Чтобы избежать таких «вырожденных» случаев, вводят следующие понятия.
являются (ориентированными) рёбрами.Циклом называют путь, в котором первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют число составляющих его рёбер. Заметим, что если вершины u и v являются концами некоторого ребра, то согласно данному определению, последовательность (u, v, u) является циклом. Чтобы избежать таких «вырожденных» случаев, вводят следующие понятия.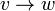 ведёт от вершины v к вершине w. Смешанный графСмешанный граф G — это граф, в котором некоторые рёбра могут быть ориентированными, а некоторые — неориентированными. Записывается упорядоченной тройкой G: = (V, E, A), где V, E и A определены так же, как выше.
ведёт от вершины v к вершине w. Смешанный графСмешанный граф G — это граф, в котором некоторые рёбра могут быть ориентированными, а некоторые — неориентированными. Записывается упорядоченной тройкой G: = (V, E, A), где V, E и A определены так же, как выше. . При этом, x область определения функции, а y - область значений. Эта функциональная зависимость между элементами множеств. х и y. функцию можно задать аналитически, как:
. При этом, x область определения функции, а y - область значений. Эта функциональная зависимость между элементами множеств. х и y. функцию можно задать аналитически, как: .
.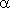 , тангенс которого равен k. Поэтому, коэффициент пропорциональности называется также угловым коэффициентом.
, тангенс которого равен k. Поэтому, коэффициент пропорциональности называется также угловым коэффициентом.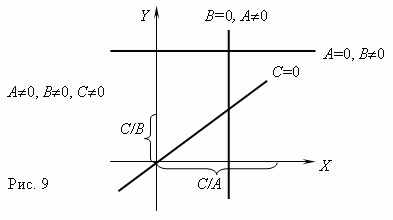
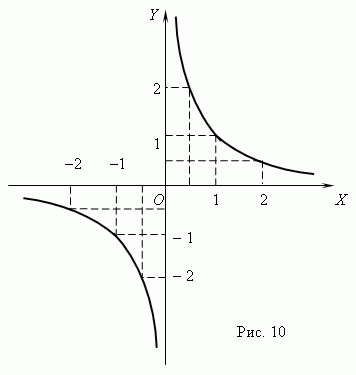 График обратной пропорциональности – гипербола. У этой кривой две ветви..
График обратной пропорциональности – гипербола. У этой кривой две ветви.. 0, область значений: y
0, область значений: y 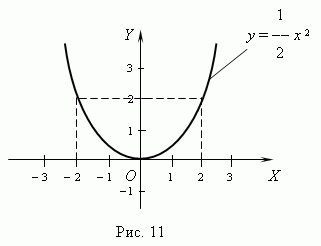 Квадратичная функция. Это функция: y = ax 2 + bx + c, где a, b, c - постоянные, a
Квадратичная функция. Это функция: y = ax 2 + bx + c, где a, b, c - постоянные, a 
 Основные характеристики и свойства квадратной параболы:
Основные характеристики и свойства квадратной параболы: < x +
< x +  R), а область
R), а область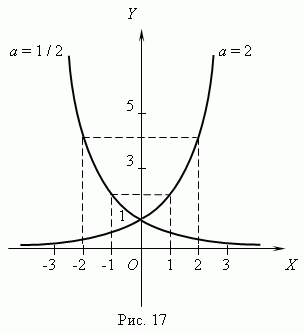 Показательная функция. Функция y = ax, где a - положительное постоянное число, называется показательной функцией. Аргумент x принимает любые действительные значения;
Показательная функция. Функция y = ax, где a - положительное постоянное число, называется показательной функцией. Аргумент x принимает любые действительные значения; Основные характеристики и свойства логарифмической функции:
Основные характеристики и свойства логарифмической функции: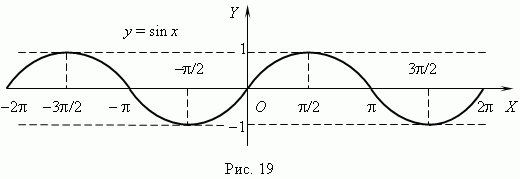
 /2
/2
 y
y  и
и 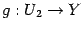 , где
, где 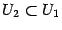 , то имеет смысл "сквозное отображение"
, то имеет смысл "сквозное отображение" 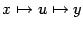 из
из  в
в  , заданное формулой
, заданное формулой 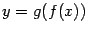 ,
,  , которое называется композицией функций
, которое называется композицией функций 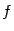 и
и 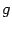 и обозначается
и обозначается 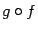 .
.
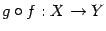 ,
, 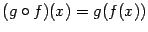 при всех
при всех 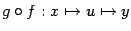 "сложено" из отображений
"сложено" из отображений  и
и  ).
). 1
1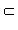 [0; 1], y
[0; 1], y 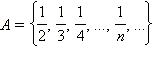 и
и 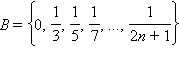 счётны и потому равномощны. В самом деле, установим взаимно однозначное соответствие между ними по следующему правилу:
счётны и потому равномощны. В самом деле, установим взаимно однозначное соответствие между ними по следующему правилу:

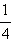 ...
... 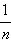 ... ↕ ↕ ↕ ↕ ↕ ↕ ↕ N 1 2 3... n... ↕ ↕ ↕ ↕ ↕ ↕ ↕ B 0
... ↕ ↕ ↕ ↕ ↕ ↕ ↕ N 1 2 3... n... ↕ ↕ ↕ ↕ ↕ ↕ ↕ B 0  ...
... 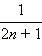 ...
... доказательство этой теоремы принадлежит немецкому математику Георгу Кантору.
доказательство этой теоремы принадлежит немецкому математику Георгу Кантору.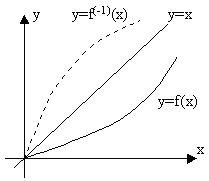
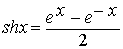 ;
; 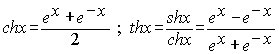 ;
; 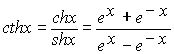 .
.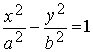
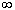 < t <
< t < 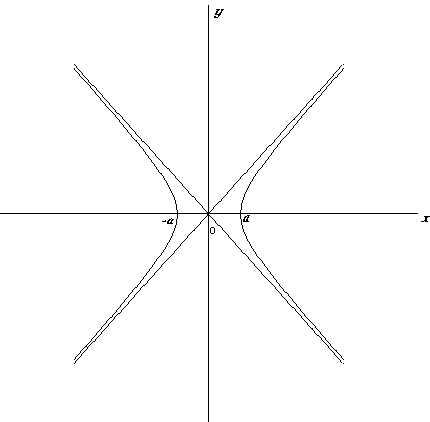
 t
t 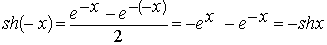 .
.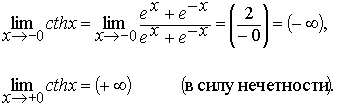
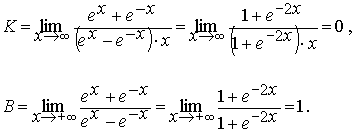
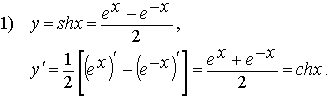
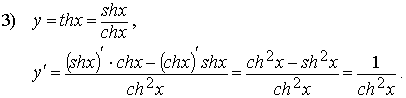

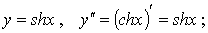 2)
2) 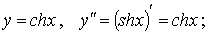
 4)
4) 

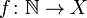 из множества натуральных чисел
из множества натуральных чисел 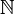 в заданное множество X называется последовательностью (элементов множества X).
в заданное множество X называется последовательностью (элементов множества X).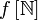 множества X, которое образовано элементами последовательности, называется носителем последовательности: пока индекс пробегает множество натуральных чисел, точка, «изображающая» последовательность, «перемещается» по носителю.
множества X, которое образовано элементами последовательности, называется носителем последовательности: пока индекс пробегает множество натуральных чисел, точка, «изображающая» последовательность, «перемещается» по носителю.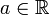 называется пределом числовой последовательности
называется пределом числовой последовательности 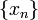 , если последовательность
, если последовательность 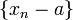 является бесконечно малой, т. е. все её элементы, начиная с некоторого, по модулю меньше любого заранее взятого положительного числа.
является бесконечно малой, т. е. все её элементы, начиная с некоторого, по модулю меньше любого заранее взятого положительного числа.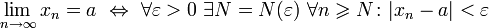
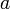 , её называют сходящейся к этому числу. В противном случае, последовательность называют расходящейся. Если к тому же она неограниченна, то её предел полагают равным бесконечности.
, её называют сходящейся к этому числу. В противном случае, последовательность называют расходящейся. Если к тому же она неограниченна, то её предел полагают равным бесконечности.