Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение прямой, проходящей через две различные точки на плоскости
Если прямая проходит через две точки A(x1, y1) и B(x2, y2), такие что x1 ≠ x2 и y1 ≠ y2 то уравнение прямой можно найти, используя следующую формулу
Вопрос 15 Вопрос 16 Уравнение прямой в отрезках Уравнение прямой линии, пересекающей ось
В этом виде невозможно представить прямую, проходящую через начало координат. Нормальное уравнение прямой
где Расстояние точки A (x 1, y 1) до прямой Ax + By + C = 0 есть длина перпендикуляра, опущенного из этой точки на прямую. Она определяется по формуле
Правило. Чтобы определить расстояние точки A (x 1, y 1) до прямой Ax + By + C = 0, нужно привести уравнение прямой к нормальному виду, взять левую часть полученного уравнения и подставить в нее вместо текущих координат координаты данной точки. Абсолютная величина полученного числа и даст искомое расстояние: Расстояние от точки до прямой есть всегда величина положительная. Кроме расстояния от точки до прямой, рассматривается еще так называемое отклонение точки от прямой. Отклонение Расстояние от точки до прямой есть абсолютная величина отклонения этой точки от прямой. Вопрос 17 Эллипс пересечение плоскости и кругового цилиндра или как ортогональную проекцию окружности на плоскость.
· · · · · ·
Каноническое уравнение Для любого эллипса можно найти декартову систему координат такую, что эллипс будет описываться уравнением (каноническое уравнение эллипса):
Оно описывает эллипс с центром в начале координат, оси которого совпадают с осями координат. Если же в правой части стоит единица со знаком минус, то получившееся уравнение:
описывает мнимый эллипс. Изобразить такой эллипс в действительной плоскости невозможно. Вопрос 18 Гипербола Гипербола — это плоская кривая второго порядка, которая состоит из двух отдельных кривых, которые не пересекаются.Формула гиперболы y = k/x, при условии, что k не равно 0. То есть вершины гиперболы стремятся к нолю, но никогда не пересекаются с ним. Гипербола — это множество точек плоскости, модуль разности расстояний которых от двух точек, называемых фокусами, есть величина постоянная. Основные понятия
1. Гипербола состоит из двух отдельных кривых, которые называют ветвями. 2. Ближайшие друг к другу точки двух ветвей гиперболы называются вершинами. 3. Кратчайшее расстояние между двумя ветвями гиперболы называется большой осью гиперболы. 4. Середина большой оси называется центром гиперболы. 5. Расстояние от центра гиперболы до одной из вершин называется большой полуосью гиперболы. Обычно обозначается a. 6. Расстояние от центра гиперболы до одного из фокусов называется фокальным расстоянием. Обычно обозначается c. 7. Оба фокуса гиперболы лежат на продолжении большой оси на одинаковом расстоянии от центра гиперболы. Прямая, содержащая большую ось гиперболы, называется действительной или поперечной осью гиперболы. 8. Прямая, перпендикулярная действительной оси и проходящая через её центр, называется мнимой или сопряженной осью гиперболы. 9. Отрезок между фокусом гиперболы и гиперболой, перпендикулярный к её действительной оси, называется фокальным параметром. o Расстояние от фокуса до асимптоты гиперболы называется прицельным параметром. Обычно обозначается b. o Каноническое уравнение гиперболы в декартовых координатах: x2 / a2 - y2 / b2 = 1 o Уравнение касательной к гиперболе, заданной каноническим уравнением, имеет вид: xox / a2 - yoy / b2 = 1 или y = yo + (b2xo)(x - xo) / (a2yo) o Уравнение нормали к гиперболе имеет вид: y = yo - (a2yo)(x - xo) / (b2xo) Некоторые типы гипербол
Гиперболу, у которой a = b, называют равнобочной. Равнобочная гипербола в некоторой прямоугольной системе координат описывается уравнением: xy = a2 / 2, при этом фокусы гиперболы располагаются в точках (a, a) и (−a,−a). Вопрос 19 Параболой называется геометрическое место точек в плоскости, равноудаленных от данной точки F, называемой фокусом и данной прямой, называемой директрисой. Каноническое уравнение параболы: У2=2рх, где р – расстояние от фокуса до директрисы (параметр параболы) Если вершина параболы С (α, β), то уравнение параболы (у-β)2=2р(х-α) Если фокальную ось принять за ось ординат, то уравнение параболы примет вид: х2=2qу Свойства параболы:1) Парабола имеет ось симметрии (ось параболы). Точка пересечения параболы с осью называется вершиной параболы. Если парабола задана каноническим уравнением, то ее осью является ось Ох, а вершиной – начало координат.2) Вся парабола расположена в правой полуплоскости плоскости Оху. Множество точек плоскости, для которых отношение е расстояния до некоторой фиксированной точки к расстоянию до некоторой прямой есть величина постоянная, представляет собой эллипс (при e <1), гиперболу (при e >1) или параболу (при е =1).
Вопрос 20. Матрица размеров mxn. Квадратная матрица. Частные случаи (треугольная, диагональная, скалярная, единичная матрицы). Линейные операции над матрицами (сложение и умножение на число) и их свойства. Умножение двух матриц. Свойства операции умножения матриц. Ответ: Любая прямая, перпендикулярная плоскости, называется нормалью к плоскости, а любой ненулевой вектор на такой прямой мы будем называть нормальным вектором плоскости. Из определения видно, что нормальный вектор у фиксированной плоскости определяется не однозначно. Все нормальные векторы одной плоскости коллинеарны друг другу и поэтому получаются один из другого умножением на число, отличное от нуля. Для того чтобы из параллельных плоскостей выбрать одну, достаточно задать точку, через которую проходит эта плоскость. Итак, если у плоскости известны нормальный вектор и точка, через которую она проходит, то плоскость определена однозначно. Ур.плоскости через нормальный вектор
3) Ax + By + D = 0 - параллельна оси Oz; 4) Cz + D = 0 - параллельна оси Oxy; 5) By + D = 0 - параллельна оси Oxz; 6) Ax + D = 0 - параллельна оси Oyz; 7) Ax + By + Cz = 0 - проходит через начало координат; 8) By + Cz = 0 - проходит через ось Ox; 9) Ax + Cz = 0 - проходит через ось Oy; 10) Ax + By = 0 - проходит через ось Oz; 11) z = 0 - плоскость Oxy; 12) y = 0 - плоскость Oxz; 13) x = 0 - плоскость Oyz. Векторное уравнение плоскостиПусть r -- радиус-вектор текущей точки 1) пересекаются 2) параллельны (но не совпадают) 3) совпадают Если плоскости заданы уравнениями 1)
Вопрос21 Уравнение плоскости, проходящей через данную точку, параллельно 2м неколлинеарным векторам. Уравнение плоскости, проходящей через 3 данные точки. Уравнение плоскости «в отрезках». Нормальное уравнение плоскости.
Уравнение плоскости по точке и двум неколлинеарным векторам В векторном виде
Уравнение плоскости в отрезках где a, b, c - величины отрезков, отсекаемых плоскостью на осях координат.
Приведение общего уравнения плоскости к нормальному виду:
Вопрос22 Различные виды уравнений прямой в пространстве (параметрические, канонические, через 2 точки, общие) Направляющий вектор прямой, заданной общими уравнениями. Уравнения прямой по двум точкам
Векторно-параметрическое уравнение прямой
|
|||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 534; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.140.5 (0.032 с.) |

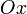 в точке
в точке  и ось
и ось  в точке
в точке  :
:

 — длина перпендикуляра, опущенного на прямую из начала координат, а
— длина перпендикуляра, опущенного на прямую из начала координат, а 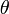 — угол (измеренный в положительном направлении) между положительным направлением оси
— угол (измеренный в положительном направлении) между положительным направлением оси 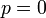 , то прямая проходит через начало координат, а угол
, то прямая проходит через начало координат, а угол  задаёт угол наклона прямой.
задаёт угол наклона прямой.




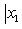


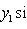


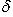 данной точки от данной прямой есть расстояние от этой точки до прямой, которому приписывается знак плюс, если точка и начало координат находятся по разные стороны от прямой, и знак минус, если точка и начало координат находятся по одну сторону от прямой.
данной точки от данной прямой есть расстояние от этой точки до прямой, которому приписывается знак плюс, если точка и начало координат находятся по разные стороны от прямой, и знак минус, если точка и начало координат находятся по одну сторону от прямой.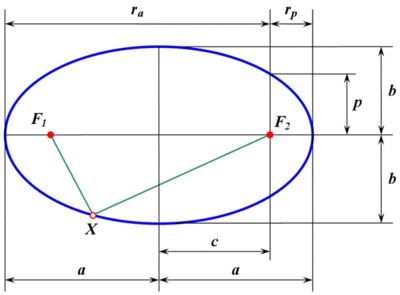
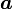 — большая полуось;
— большая полуось; — малая полуось;
— малая полуось; — фокальный радиус (полурасстояние между фокусами);
— фокальный радиус (полурасстояние между фокусами);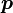 — фокальный параметр;
— фокальный параметр; — перифокусное расстояние (минимальное расстояние от фокуса до точки на эллипсе);
— перифокусное расстояние (минимальное расстояние от фокуса до точки на эллипсе);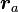 — апофокусное расстояние (максимальное расстояние от фокуса до точки на эллипсе);
— апофокусное расстояние (максимальное расстояние от фокуса до точки на эллипсе);


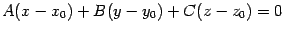 Общее уравнение плоскости
Общее уравнение плоскости Частные случаи общего уравнения плоскости: 1) By + Cz + D = 0 - параллельна оси Ox; 2) Ax + Cz + D = 0 - параллельна оси Oy;
Частные случаи общего уравнения плоскости: 1) By + Cz + D = 0 - параллельна оси Ox; 2) Ax + Cz + D = 0 - параллельна оси Oy; плоскости
плоскости  ,
, 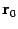 -- радиус-вектор точки
-- радиус-вектор точки  . Тогда уравнение (11.2) можно переписать в виде
. Тогда уравнение (11.2) можно переписать в виде  Такое уравнение обычно называют векторным уравнением плоскости
Такое уравнение обычно называют векторным уравнением плоскости  , то они:
, то они:


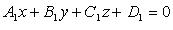 и
и 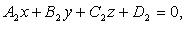 то случаи 1 - 3 имеют место, когда:
то случаи 1 - 3 имеют место, когда: 2)
2)  3)
3) 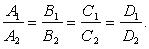
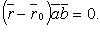 В координатах
В координатах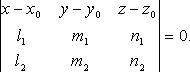 Уравнение плоскости по трем точкам В векторном виде
Уравнение плоскости по трем точкам В векторном виде  В координатах
В координатах  или
или 
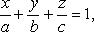
 где
где  - углы, образуемые нормальным вектором плоскости с осями координат; p - расстояние от начала координат до плоскости.
- углы, образуемые нормальным вектором плоскости с осями координат; p - расстояние от начала координат до плоскости. Здесь
Здесь  - нормирующий множитель плоскости, знак которого выбирается противоположным знаку D, если
- нормирующий множитель плоскости, знак которого выбирается противоположным знаку D, если 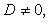 произвольно, если D = 0.
произвольно, если D = 0.
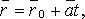 где
где  - фиксированная точка, лежащая на прямой;
- фиксированная точка, лежащая на прямой; 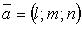 - направляющий вектор.Канонические уравнения прямой
- направляющий вектор.Канонические уравнения прямой