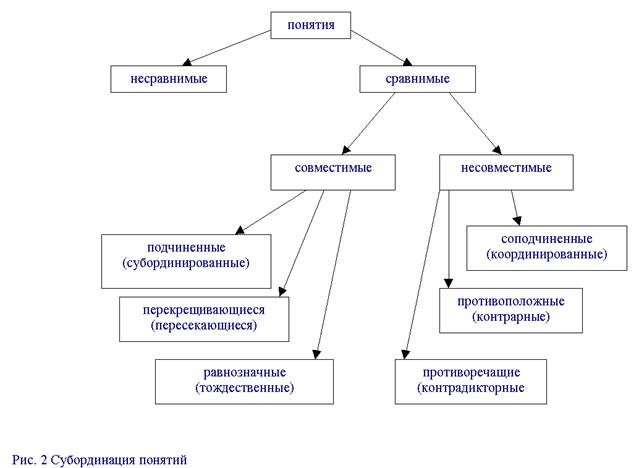
Типы отношений между понятиями

Логические операции, позволяющие делать определенные выводы и доказывать какие-то утверждения, основываются, как уже отмечалось ранее, на связях и отношениях разных понятий. Такие связи очень многообразны и на их изучение, в конечном счете, и направлена вся наука, вся познавательная деятельность человека вообще. Часть из них изучается только логикой и никогда не делается предметом специального внимания других наук. Сейчас речь пойдет именно о таких связях и отношениях; они могут быть обусловлены как содержанием понятий, так и их объемом. С некоторыми из них мы уже сталкивались.

Классификация понятий с точки зрения взаимоотношений между ними начинается с разделения их на сравнимые, которым свойственны чисто логические связи и отношения, и несравнимые, у которых таких связей нет вообще. К несравнимым относятся, например, "трамвай" и "треугольник", "осень" и "обратная сторона Луны", "алмаз" и "паровозный гудок"; их отличительная черта состоит в том, что ни в их содержании, ни в их объеме нет общих элементов. Поэтому, зная что-то об одном из них, нельзя делать выводы о другом - отсутствие логических связей не позволяет проложить переход между ними. Следует, правда, помнить, что в целом ряде случаев и близкие по смыслу понятия несравнимые. Так, зная скорость, легко определить пройденное расстояние, а по цене можно определить прибыль. Однако для получения таких выводов понадобится к правилам и законам логики прибавить законы других наук - в данном случае механики и экономики, - а также знание некоторых конкретных условий: времени движения и, соответственно, количества проданного товара. Без этого нельзя было бы умозаключать от скорости к пройденному пути и от цены к прибыли. Несравнимыми понятия становятся из-за отсутствия чисто логических связей и отношений, и сейчас речь идет только о них. Они обязательно имеются у сравнимых понятий, потому что у них есть общие элементы в объеме и (или) содержании. И делать умозаключения относительно их можно, опираясь на одни лишь формальные особенности, взятые из их определений. Мы уже не раз встречались с ними, например, когда говорили о законе исключенного третьего. Если нам удалось доказать, что, допустим, примененное на полях удобрение не является органическим, то тогда мы в состоянии уверенно отнести его к числу минеральных.

Сравнимые понятия подразделяются на два вида - совместимые и несовместимые, а каждый из этих в свою очередь распадается еще на три разновидности. Начнем с понятий совместимых. К ним относятся: равнозначные (тождественные), перекрещивающиеся (пересекающиеся) и подчиненные (субординированные) понятия.

Отношение равнозначности (тождества). Равнозначные понятия имеют одинаковый объем, но разное содержание; ими охватываются одни и те же предметы, но задаются эти предметы через разные признаки. Так, если мы сначала будем говорить о равносторонних треугольниках, а потом обратимся к равноугольным треугольникам, то ясно, что предмет обсуждения не изменится, просто мы будем его иначе называть. Графически равнозначность изображается в виде двух кругов, слившихся в один (см. рис. 2).

Отношение перекрещивания (пересечения). Перекрещивающиеся понятия имеют разное содержание, но объемы их частично совпадают и в то же время частично не совпадают. Понятия "домашнее животное" и "коза" именно таковы: с одной стороны, козы бывают не только домашними, и среди домашних животных, с другой стороны, имеются не только козы. Название "перекрещивающиеся" объясняется тем, что изображающие их круги частично накладываются; общий для обоих кругов сектор означает, что есть животные, которые входят в оба понятия, каковыми в нашем примере являются домашние козы (см. рис. 2).

Отношение подчинения (субординации). Понятия, находящиеся в отношении подчинения, имеют одинаковые элементы в содержании, а объем одного (подчиненного) полностью входит в объем другого (подчиняющего). В принципе это то же самое, что и отношение ограничения (обобщения), но только здесь рассматривается обычно не более двух понятий. В теории определения подчиняющее понятие называют также родовым или родом, подчиненное - видовым или видом, а признак, по которому вид выделяется из рода, - видообразующим. В качестве примера назовем "инструмент" и "молоток". При графическом изображении видовое понятие помещается внутри родового (см. рис. 2).

 

 

К несовместимым понятиям относятся противоречащие (контрадикторные) противоположные (контрарные) и соподчиненные (координированные) понятия. В содержании таких понятий имеются отдельные общие признаки, но они соединяются в каждом из них так, что делают соответствующие понятия взаимоисключающими.

Отношение противоречия (контрадикторности). В разделе о законах логики уже говорилось об отношении противоречия и противоположности между высказываниями. Такие отношения возможны и между понятиями. Противоречащими называются понятия, когда у одного из них имеется тот или иной признак, а у другого он отрицается (признак вообще-то отмечается в содержании того и другого, но по-разному). Например, "белый" - "небелый", "добрый" - "недобрый". Для них характерно, что они делят весь массив родственных предметов и явлений строго на две части: на тех, что обладают данным признаком, и тех, которые его не имеют; ничего промежуточного между ними, как легко догадаться, не бывает. Именно поэтому их отношения регулируются законом исключенного третьего (см. раздел об основных законах логики). Круговые схемы для несовместимых понятий требуют изображать родовое понятие (хотя оно может не быть даже упомянуто). В нашем примере такой круг обозначает цвет (поступок) вообще, а каждой из половинок соответствует одно из противоречащих понятий (см. рис. 2). Само собой, очевидно, что разделение круга пополам не означает, будто число белых и небелых вещей в природе одинаково. Такая количественная характеристика вообще не получает выражения при использовании кругов Эйлера. Ими отмечается только, что противоречащих понятий всего два и нет иных.

Отношение противоположности (контрарности). Противоположные понятия являются видами одного и того же рода, но одно из них обладает каким-то признаком, а другое не только не обладает им, но и имеет сверх того еще и признак, несовместимый с данным, направленный против него. Таковы "белое" и "черное", "добро" и "зло". Предметов, явлений или поступков, относимых одновременно к тому и другому, не бывает. Однако в отличие от отношения противоречия могут быть такие объекты, которые не входят ни туда и ни сюда. Если общее родовое понятие означает цвет вообще, то тогда в отображающем его круге выделяются два сектора; они расположены друг против друга и соответствуют понятиям белого и черного, оставшийся промежуток отображает все остальные цвета (см. рис. 2).

Отношение соподчинения (координации). Соподчиненные понятия имеют в содержании общие элементы, благодаря которым все вместе входят в родовое понятие, но общих элементов в их объемах нет. Скажем, дуб, ель, береза - разновидности дерева, изображающие их круги должны помещаться внутри круга, изображающего объем понятия "дерево", но они ни в коем случае не могут пересекаться, потому что не существует деревьев, которые были бы и дубом, и елью, и березой одновременно (см. рис. 2). В графическом изображении соподчинения есть некоторое сходство с противоположностью. Так, "утро" и "вечер" противоположны, но их можно рассматривать и в качестве соподчиненных, охватываемых наряду с "днем" и "ночью" родовым для них понятием "время суток". Все они могут быть изображены четырьмя кругами, внесенными в один общий, и это будет правильно. Однако в этом случае не получит выражения наличие у них попарной противоположности. Конечно, когда от нее можно отвлечься, то прибегать к такому изображению противоположных понятий не будет ошибкой. Если же пренебрегать ею при анализе мысли нельзя, то тогда надо брать круговые схемы для противоположных понятий. Правда, и в этом случае выигрыш в одном отношении обернется упрощением с другой точки зрения: средний участок между противоположными секторами будет представлять множество (возможно несовместимых, соподчиненных) понятий (в нашем примере "день" и "ночь" станут неразличимыми).

Вообще, используя круговые схемы, следует помнить: содержательная характеристика понятий при этом способе придавать наглядность отношениям понятий получает очень слабое выражение. Круги Эйлера удобны для изображения соотношений по объему. Несмотря на внешнюю простоту и незатейливость, при анализе сложных и запутанных высказываний, они оказываются порой просто незаменимыми. Да и уяснение теоретических вопросов в самой логике существенно упрощается.

Определение понятий

В научной литературе определение иногда называют также дефиницией. Определение предназначено для того, чтобы сформулировать в явном виде и зафиксировать содержание понятия, назвать те признаки или свойства предмета, которые станут объектом внимания в рассуждении и как бы заменят на время сам предмет. Ведь вообще все признаки любой вещи нельзя даже перечислить, не говоря уже о том, чтобы внести их все в определение. Не всегда предмет обсуждения задается в отчетливой форме. Иногда предполагается, что читатель или собеседник в состоянии сам догадаться, какие черты и особенности обсуждаемых явлений затронуты при рассмотрении. Правда, история науки знает несчетное множество примеров того, как обманчива бывает такая самоочевидность. Порой многие поколения ученых, введенные ею в заблуждение, либо бесплодно ищут там, где ничего нет, либо, наоборот, долго не замечают того, что лежит перед глазами.

Наверное, самый поучительный в этом отношении урок доставили многовековые стремления математиков доказать постулат о параллельных, закончившиеся созданием неевклидовых геометрий. Уже после того, как была позади долгая стадия поисков и сомнений, и предстояло осмысливать достигнутые необычные результаты, неожиданно обнаружилось, что в доказательствах не было самого главного - определения того, о чем шла речь в первую очередь, то есть определения прямой линии. И поскольку это так, в него автоматически превратились аксиомы, на которые опиралось доказательство: 1) между двумя точками можно провести прямую линию и притом только одну, 2) прямая - кратчайшее расстояние между точками. Все причудливые построения, допускающие несколько параллельных прямых, проходящих через одну и ту же точку (пространство Лобачевского), или, наоборот, не допускающие ни одной (пространство Римана), в логическом отношении совершенно безупречны, но они, оказывается, относятся не к прямой в обычном смысле этого слова, а к кратчайшей линии между двумя точками, которую можно провести между ними только одну. Иными словами, неевклидовы геометрии говорят о пространствах, в которых линии обладают только этими двумя свойствами и не имеют больше никаких иных. Очистить наши представления о линиях от наслоений чувственного опыта и провести строгую дедукцию с такими искусственно созданными понятиями могли лишь гениальные математические умы, настоящие титаны мысли. Однако в дальнейшем обнаружилось, что полученные результаты имеют простое наглядное представление. Линии, удовлетворяющие только названным выше аксиомам, скажем, на шаре представляют собой всем известные меридианы, и среди них действительно нет и не может быть таких, которые не пересекаются (нет параллельных, как этого и требует геометрия Римана). А на так называемой псевдосфере такие же линии могут, наоборот, не пересекаться вообще (у каждой есть много параллельных - геометрия Лобачевского).

Неевклидовы геометрии - не единственный случай, когда побочный результат научных поисков стал главным достижением. Но факт остается фактом: появились они из-за того, что не было и нет определения прямой и точки. Более того, такие определения невозможно сформулировать, так как не существует ничего более простого, чем они.

Разумеется, далеко не всегда отсутствие определения может столь радикально обогатить наши привычные представления. Гораздо чаще нежелание обстоятельно продумать и сформулировать точную дефиницию порождает бестолковое топтание на месте. Во избежание недоразумений, для достижения точности и полной ясности в рассуждениях, выводах, доказательствах, при анализе высказываний и тем более в спорах определения совершенно необходимы. Они вообще представляют собой один из атрибутов научного знания. Нельзя было бы создать ни одной теории без строго определенных понятий и категорий. Ими обязательно пользуется каждая наука. Однако теория самого определения разрабатывается только в логике. В ней формулируются правила определения понятий и указываются возможные ошибки, когда эти правила не соблюдаются. Кроме того, логика выявляет виды определения и тех приемов, которые могут его заменить, когда строгая формулировка затруднительна или вообще невозможна.

Наиболее совершенным является определение через ближайший род и видовое отличие. При его формулировании сначала указывается понятие более широкое (род), чем то, которое надо определить (вид), затем называют отличительный признак (видовое отличие), с помощью которого определяемый вид предметов выделяется среди других, входящих в тот же род. Например, если мы определим столицу как город, в котором находятся правительственные учреждения страны, то тогда родом для "столицы" будет "город", а видовым отличием, то есть признаком, по которому главный город в государстве можно отличить от остальных городов, будет служить то обстоятельство, что он является местом пребывания правительственных органов управления страной.

В определениях через ближайший род и видовое отличие очень четко задаются соотношения понятий по объему. Благодаря этому с ними легче всего совершать логические операции и процедуры. Вообще всякая наука стремится к тому, чтобы скомпоновать всю совокупность своих понятий в единую систему, составленную из нескольких последовательно нисходящих родовидовых ярусов: самые фундаментальные понятия разветвляются на некоторое число видов, те в свою очередь дробятся на подвиды и так далее. Обычно это удается достигнуть в более или менее полной форме в относительно законченных разделах научного знания, когда выявлены существенные необходимые связи, пронизывающие всю толщу изучаемых явлений, процессов, а также взаимодействий и взаимовлияний между ними, в которых они участвуют. В этом случае каждое из изучаемых данной наукой явлений вписано в общую картину в качестве всесторонне изученного фрагмента, становится понятным и прогнозируемым: известны факторы, под влиянием которых оно преобразуется, и одновременно точно установлены и легко прослеживаются следствия, которые вызывает само данное явление.

Близким по удобству использования к предыдущему является генетическое определение. В нем указывается способ создания или путь возникновения того или иного явления. Иногда заданные таким образом черты и особенности могут служить видообразующими признаками, и тогда создается та же самая родовидовая дефиниция. Например, оксиды в химии определяют как сложные вещества, возникающие в результате соединения атомов кислорода с атомами другого вещества. О возникновении здесь хотя и говорится, но указание на него не имеет принципиального характера с точки зрения логической теории определения: в нем все равно задается более широкое понятие сложного химического вещества и отмечается видообразующий признак - соединение атомов кислорода с другими атомами, по которому оксиды могут быть отличены от остальных сложных химических веществ. Выделяемые таким способом вещества существуют не только в процессе возникновения, и их определения при желании можно дать без упоминания процесса возникновения, просто отметить наличие того и другого атома в составе оксида и все.

О чисто генетических определениях, строго говоря, можно вести речь лишь применительно к процессам или же к таким их результатам, которые как бы сохраняют в себе свою прошлую историю. Так лавой в геологии называют огненно-жидкий поток расплавленных горных пород, изливающихся из глубинных зон Земли во время вулканических извержений. Формально выражаясь, можно, конечно, и здесь найти базовое родовое понятие - расплавленные глубинные горные породы. Но лава не отделяется под землей от остального расплава; она становится таковой в момент выхода на поверхность и перестает ею быть после того, как остынет и окаменеет.

Наш мир, как известно, наполнен процессами. Одни из них скоротечны, как, например, шаровая молния или набухающая почка. Другие протекают медленно. Указание на происхождение может иметь немаловажное познавательное значение и для не изменяющихся объектов тоже. Это бывает тогда, когда прошлые этапы сказались на существующих свойствах, и определяют облик носящих эти свойства явлений. К примеру, в ряде языков имеются так называемые субстантивированные прилагательные - существительные, возникшие из прилагательных, - "столовая", "парикмахерская", "портной" и множество других. Хотя ими обозначают предметы, а не свойства, и с этой точки зрения они относятся к существительным, оставаясь к тому же неизменными в качестве таковых, тем не менее, их происхождение запечатлелось на их грамматических особенностях, они по-прежнему подчиняются правилам для прилагательных. Поэтому выделение таких слов в особую грамматическую категорию через указание на их генезис оправдано и характеризует их с существенной стороны. Вообще этимология слова, обозначающего понятие, всегда является полезной дополнительной информацией к определениям и широко используется далеко за пределами языкознания.

В целом ряде случаев, как уже говорилось ранее, нет необходимости и не требуется строго задавать анализируемые явления. Иногда достаточно всего лишь надежно отделить их от всего остального, обозначив тем или иным способом какие-либо неотъемлемые признаки, чтобы исключить путаницу с другими явлениями. Тогда используют так называемые приемы, сходные с определением. Среди таковых можно выделить контекстуальные и остенсивные определения, объяснения, характеристики, описания.

При контекстуальном задании не дается специально сформулированной дефиниции, но из сообщения, сделанного письменно или устно, все равно ясно, что подлежит обсуждению. Так, описывая поведение того или иного человека в стрессовой ситуации, тем самым попутно задают и склад его характера, и особенности психики. Собирать такие, разбросанные, может быть, по тексту характеристики и делать из них выводы вполне допустимо и делается это часто. Только надо помнить, что фрагментарное изложение, не продуманное специально в отношении деталей, все-таки чревато неточностями и искажениями. Поэтому безупречные с логической точки зрения выводы, полученные на основе таких определений, могут оказаться ошибочными из-за шаткой почвы, на которой они покоятся.

Иногда удобно пользоваться так называемыми остенсивными определениями. В этом случае вместо выявления существенных признаков определяемого явления указывают на само явление как на образец. Многие, наверное, знают, как иногда объясняют слово "сенсация" - когда человек покусал собаку, а не собака человека. Поначалу остенсивным определением назывался прием, к которому вынуждены прибегать люди, говорящие на разных языках. Не понимая слов, они используют жестикуляцию, показывая руками на предметы и одновременно называя их.

Есть много вещей, которые невозможно определить. Так, часто говорят, что нет возможности дать строгое определение произведению искусства. И действительно, никто не в состоянии указать формальные признаки, по которым любой мог бы уверенно сказать, является ли данное произведение подлинным шедевром или его надо считать посредственным. Юристы порой сталкиваются с ситуацией, когда надо точно определить, что такое порнография, но из попыток дать дефиницию ничего не получается. Надо сказать, в искусствознании вообще довольно часто образец произведения какого-либо рода нельзя заменить его определением. Но и в науке такие обстоятельства тоже могут иметь место. В философско-методологической литературе иногда используют понятие "парадигма". Ему давали много разных определений. По своему смысловому значению оно близко к тому, что называют остенсивным определением. Этот термин встречается уже у Аристотеля. Он называет парадигмой обобщения, делаемые на основе только одного, но очень, так сказать, яркого в своем роде явления. В настоящее время под парадигмой имеют в виду такое единичное явление, которое концентрирует в себе родовые признаки, тем самым рельефно высвечивая в единичном общее. Оно становится как бы шаблоном или моделью, по которой можно судить об остальных представителях того же класса явлений, процессов, действий.

Одним из приемов, сходных с определением, является объяснение. Оно может не столько заменять определение того или иного явления, сколько дополнять его или делать его понятным. Это достигается за счет того, что незнакомые широкой публике термины выражают через другие, известные всем. Возьмем термин "гипостазирование". Он станет понятен, если мы скажем: этим словом обозначают ошибку мышления, заключающуюся в том, что оно принимает чисто мыслимые сущности за реально существующие, подобно тому, как Платон наделял самостоятельным бытием любое общее понятие.

Методов объяснения очень много - от указания причин и создания моделей до проведения аналогий. Этими методами занимается специальная теория объяснения. То, что предстоит объяснить, в ней называют экспланандом, совокупность же объясняющих положений - экспланансом. Очень часто составители толковых словарей заменяют строгие научные определения терминов своими, объяснительными. Может, например, удивить, что в известном словаре С.И. Ожегова при определении, допустим, хлопчатника, вместо отнесения его, как делается в ботанике, к многолетней разновидности растений семейства мальвовых, отмечается, что это - растение, семена которого покрыты пушистыми волосками, дающими хлопчатник. В этом нет отступления от научности. Данные определения являются объяснительными. Их назначение в том, чтобы сделать термины понятными неспециалистам.

В тех случаях, когда нет возможности или необходимости дать точное определение, может использоваться также и характеристика. С ее помощью указывают на черты или особенности предмета, важные в каком-либо отношении. Ознакомление с предметом через них может быть достаточно полным и всесторонним, несмотря на то, что такие способы не вполне удовлетворяют требованиям, предъявляемым к определениям. Характеристики дают как целым классам вещей, так и отдельным явлениям и процессам. Такой способ ознакомления может не заменять определение, а дополнять и углублять его. Широко распространены характеристики, даваемые людям. В них отмечаются их должностные или профессиональные достоинства, компетентность и прочее. Важнейшее требование к характеристикам состоит в том, что они должны быть объективны.

Много сходного у характеристики и с описанием. Обыкновенно оно дается индивидуальным предметам, для которых нельзя указать родовидовые признаки. Бывают описания редких драгоценностей. При введении государственной символики, а также учреждении новых медалей и орденов им принято давать описания. Существуют описания государственных границ и различных географических точек. До изобретения фотографии широко использовались приметы, с помощью которых описывали разыскиваемых лиц.

Описание выиграет, если перечисленные в нем признаки будут систематизированы и изложены последовательно. Как при характеристике, так и при объяснении обязательно используются сравнения и различения. Надо сказать, эти два последних метода ознакомления с вещами и предметами вообще неотъемлемы для всей познавательной деятельности в целом и, в частности, для теории определения. Их тоже иногда называют разновидностями приемов, сходных с определением.

§9. (1) Правила определения понятий

Поскольку понятие - элементарная клетка логической мысли, то его правильное определение представляет собой одно из первых условий безошибочного рассуждения. И всякий разбор высказанных мыслей должен начинаться с определения входящих в них понятий. Существует несколько правил для задания определений, без соблюдения которых нельзя сделать мышление последовательным и определенным, а получаемые им выводы обоснованными.

1. Определение должно быть точным и ясным. Само по себе это требование достаточно банально. Нет наверно ни одной отрасли знания или области деятельности, где ясность и точность не были бы обязательными. Однако именно при образовании понятий нарушение этого правила дает себя знать непосредственнее и сильнее всего, потому что определение создает первокирпичики мышления. Несоблюдение этого правила может быть непреднамеренным, проистекающим просто из-за того, что не подумали над своими собственными словами или, может быть, вообще не придали значения определению, положившись на то, что смысл используемых понятий достаточно точно задан в контексте, то есть хорошо угадывается из общего хода изложения. Однако бывает (и не так уж редко), когда нарушение этого требования является умышленным. В политике и судебно-следственной практике это даже скорее заурядное явление. Иные лидеры сознательно прибегают к туманным, расплывчатым выражениям, когда дают обещания или рассказывают о своих целях, в результате чего невозможно понять, как увязать их слова с их делами, можно ли сделать вывод о том, что одно соответствует другому, или нет. Без точно сформулированных определений мысль не может быть логически правильной.

2. Определение должно быть соразмерным. Объемы определяющего и определяемого понятий должны быть одинаковыми. Ранее уже говорилось, что, когда у понятий один и тот же объем, но они задаются через разные признаки, то тогда такие понятия равнозначны. Совершенно очевидно, что определяющее и определяемое понятия должны быть именно таковыми. Только в этом случае знание об одном из них можно переносить на другое и при этом, с одной стороны, не произойдет переноса сделанных утверждений на лишние, не входящие в соответствующий объем, предметы, с другой стороны, и упущено ничего не будет.

Нарушение этого правила ведет к трем разновидностям ошибок. Одна из них - слишком узкое определение, когда объем определяющего понятия уже, чем определяемого. Возьмем такие выражения: "Верблюд - двугорбое животное" и "Хоботные - это слоны". На первый взгляд они кажутся правильными, но на деле верблюды бывают не только двугорбые, что же касается хоботных, то только современные хоботные исчерпываются семейством слонов, вообще же этот отряд животных включает в себя и другие семейства, например мастодонтов. Если бы мы рассматривали эти высказывания как определения, то, конечно же, пришли к ложным выводам: часть животных выпадет из рассмотрения и полученные обобщения, если бы мы стали их делать, оказались бы ограниченными.

Бывают также слишком широкие определения. В качестве примера можно указать такие: "Кража - это уголовно наказуемое преступление" и "Характер - это основа поведения человека". В них определяющие понятия являются более емкими, чем определяемые. К уголовно наказуемым деяниям относятся не только кражи. Чтобы отделить ее от остальных правонарушений, надо указать еще и на похищение имущества, причем, сделав оговорку о тайном похищении. Только тогда этот вид преступления не будет спутан, скажем, с разбоем или с ограблением. И точно так же основа поведения человека создается не только его характером, но и многим другим: мировоззрением, воспитанием, условиями жизни и т.п. В качестве характеристик приведенные высказывания возможны. Но они не могут служить определением в полном смысле этого слова. Нельзя с их помощью правильно квалифицировать преступления или дать верную оценку поведения человека.

Могут быть определения, слишком широкие в одном отношении и слишком узкие в другом. Например, предложение "Хвойное дерево - живой организм, произрастающий в тайге", содержит именно такую ошибку, если на него смотреть как на определение, поскольку в нем в качестве родового вместо растения указано более широкое понятие "живой организм". Тем самым целый ряд признаков, специфичных только для растений, отбрасывается. В то же время отнесение места произрастания хвойных деревьев только к тайге заузит определение.

3. Определение не должно быть тавтологичным (не должно образовывать круга). Тавтологичными являются всем известные бессодержательные выражения вроде "масло масляное". В них вместо объяснения или определения нужных нам явлений дается ничего не говорящая фраза, в которой просто повторяется то, что уже и без того известно или даже прямо выражено в названии.

Как отмечал в свое время Гегель, если на вопрос, что такое Бог, отвечают: Бог есть Бог, то каждый с этим соглашается, однако, тем не менее, совершенно очевидно, что этим ничего не сказано. При определении данное понятие надо выражать обязательно через другие, отличающиеся от него, точно так же, как при извлечении выводов надо получать содержательно новые высказывания, а не повторять прежние в новых выражениях.

Причем помимо прямых и явных тавтологий бывают и скрытые, так называемый логический круг. Он возникает тогда, когда определяющее понятие, хотя и отличается от определяемого, однако его задание само требует обращения к этому определяемому. Из-за этого, в конечном счете, все сводится к повторению одного и того же. Так, вращение определяют обычно как движение вокруг оси, а ось, в свою очередь, определяют как центр вращения. Получается: земля на ките, кит на воде, вода на земле.

Правда, у этого правила есть исключение. Оно относится к соотносительным понятиям (см. виды понятий). При их определении избежать логического круга невозможно. Попробуйте определить, что такое, скажем, верх. В обыденной жизни нам не приходится над этим задумываться, а коль понадобится, мы тут же можем указать пальцем, где он находится. Но при попытке выразить это понятие теоретически, то есть через другие понятия, сразу же обнаруживается, что у нас нет иного выхода, кроме указания на противоположность низу: верх есть то, что не есть низ. А низ, в свою очередь, тоже есть то, что не является верхом.

Соотносительных понятий, как уже отмечалось, довольно много: причина и следствие, материя и сознание, добро и зло и многое другое. Разъясняя трудности определения материи, Ленин подчеркивал: при формулировании этого понятия приходится ограничиваться указанием отношения между материей и сознанием, так как нет более широких понятий ни в сфере бытия, ни в сфере идеального. В итоге получается, что сознание есть свойство материи, а материя - то, что существует вне сознания.

4. Определение не должно быть отрицательным. В отрицательных определениях вместо задания признаков, составляющих содержание понятия, указывают, какой признак отсутствует. "Флейта - это не паровозный гудок" - как раз такое предложение; оно является, хотя и истинным, но никак не может рассматриваться определением, поскольку ни содержание, ни объем понятия "флейта" в нем не задаются. Формально говоря, если бы мы стали смотреть на такое высказывание как на определение, то оно оказалось бы слишком широким - в объем определяющего понятия входит абсолютно все, кроме паровозного гудка. Ограничиваясь отрицаниями относительно чего бы то ни было, можно дать верную характеристику предмету, но, как правило, содержание его полностью не раскрывается и не задается объем. Определение в строгом смысле этого слова таким путем не создается.

Однако и у этого правила тоже бывают свои исключения. Скажем, понятия "невменяемый", "несовершеннолетний" являются отрицательными и по названию, и по содержанию: не несущий ответственности за свои поступки, не достигший определенного возраста. Причем с такими понятиями можно работать, совершать над ними логические операции, применять к ним логические законы точно так же, как и по отношению к понятиям, заданным через ближайший род и видовое отличие. Надо сказать, такие понятия имеются в разных науках и образуют целый устойчивый класс. Иногда их даже указывают среди видов понятий как их особую разновидность.

Отрицание признака может однозначно задать объем и содержание тогда, когда признак, который отрицается, является универсальным в своем роде, присущ всем предметам, о которых идет речь. В этом случае отсутствие данного признака становится примечательной особенностью, подобно тому, как выделяется белая ворона среди всех остальных ворон. Чаще всего отрицание играет роль характеристики: материя - нечто несотворимое и неуничтожимое; свобода слова - неотъемлемое право каждого гражданина в демократическом обществе. Но в некоторых случаях через отрицание задаются и фундаментальные научные понятия. Так, атом определяют как неделимую частицу химического вещества. Само собой разумеется, делимость присуща абсолютно всему; атом же отчетливо выделяется среди всего остального благодаря тому, что его раздробление ведет к исчезновению химических свойств у вещества, и в этом смысле он неделим. Отрицательным является и определение параллельных как непересекающихся прямых, лежащих в одной плоскости. И здесь тоже легко проводить только пересекающиеся линии. А для того, чтобы они легли параллельно друг другу, надо прибегнуть к специальным приемам. Так что отсутствие пересечения является признаком, выделяющим параллельные линии достаточно однозначно.