Распределенность терминов в суждении

Свойства суждений определяются еще одним важным показателем - распределенностью их терминов, который играет большую роль в правилах умозаключений. Оно отображает полноту выраженных в суждении знаний о тех предметах, явлениях, свойствах, которые входят в объемы понятий субъекта и предиката, то есть об упоминаемых в суждении вещах и их свойствах. Одни из них характеризуются прямо, другие же лишь косвенно. Например, суждение "Передвижники являлись русскими художниками", с одной стороны, дает сведения непосредственно о членах Товарищества передвижных художественных выставок (все они русские художники), с другой стороны, окольным путем характеризует и русских художников того времени (часть из них была передвижниками). Точно также и суждение, допустим, "Невменяемые не привлекаются к ответственности" дает информацию как о невменяемых, о так и привлекаемых к ответственности: все невменяемые не принадлежат к числу тех, кого привлекают к ответственности, и все привлекаемые к ответственности не являются невменяемыми.

Оба термина суждения характеризуются, следовательно, и в качестве свойства предмета, и в качестве самого предмета. Но надо помнить, что характеристика такого рода зависит от многих обстоятельств и может не в одинаковой мере затрагивать оба термина.

Градаций распределенности всего две: либо мы получаем сведения обо всем объеме, либо только о части; это соответствует и делению суждений по количеству на общие и частные.

Термин суждения является распределенным, если он взят в нем во всем объеме, то есть из суждения видно, что все предметы его объема обладают (не обладают) каким-то свойством.

Термин суждения является нераспределенным, если он берется не во всем объеме - лишь часть предметов его объема обладает (не обладает) каким-то свойством.

Для распределенности имеет значение только полнота знаний об объеме. Характеризуется ли термин в утвердительной форме (ему приписывается свойство) или в отрицательной (отрицается таковое у него), не играет роли. Когда про объем понятия известно, что все его предметы не обладают таким-то свойством, то он все равно является так же распределенным, как если бы было известно, что все они обладают им. Правда, для одного и того же суждения распределенность должна иметь один и тот же смысл: характеризуется один из терминов как распределенный в качестве обладающего тем или иным свойством, тогда и другой термин тоже должен оцениваться на распределенность по признаку именно обладания свойством.

Нам осталось только рассмотреть все виды суждений и отметить распределенность терминов в каждом из них. Для этого полезно будет обращаться к рисункам 3-6, на которых воспроизводятся объемные соотношения между понятиями, играющими роль терминов в суждении.

В общеутвердительном суждении субъект всегда распределен. На это указывает квантор. Обычно стоящее на месте предиката понятие шире по объему, чем то, которое стоит на месте субъекта (рис. 3), как, например, в суждении "Каждый поэт - литератор". Предикат же, как правило, не распределен. В данном случае это видно из того, что не все литераторы поэты. Но могут быть и исключения, когда субъект (S) и предикат (P) образуют равнозначные понятия и тогда оба термина - и S, и P - распределены. Таковы суждения "Правительство - кабинет министров" и "Клептомания - болезненно навязчивое стремление к воровству". Поскольку понятия в них равнозначны, то значит, всякий кабинет министров является правительством и всякое болезненно навязчивое стремление к воровству есть клептомания. Правда, для логики, которая создает правила оперирования понятиями на основе только формы высказываний (не обращаясь к содержанию), такие исключения не имеют принципиального значения. Потому что их можно учесть лишь при знании материала, затронутого в данном суждении. Сама же форма общеутвердительного суждения твердо гарантирует только то, что часть предметов, о которых говорится в предикате, обязательно обладает свойством S. Мы будем считать, поэтому субъект общеутвердительного суждения всегда распределенным, а предикат нераспределенным.

В общеотрицательном суждении оба термина всегда распределены. Раз в нем прямо отрицается принадлежность всех предметов одного класса к предметам другого, то тем самым отрицается и принадлежность всех предметов второго к первому (рис. 4). Из-за того, что никакой кит не является рыбой, мы легко придем к выводу, что никакая рыба не является китом. Значит, в общеотрицательных суждениях оба термина характеризуются в полном объеме как не принадлежащие к какому-то классу предметов.

Частноутвердительное суждение всегда имеет нераспределенный субъект; на это указывает квантор "некоторые". Предикат тоже чаще всего не является распределенным, как в суждении "Некоторые музыканты - филателисты"; эти два понятия относятся к числу пересекающихся, поэтому часть людей одной категории обладает свойством другой, а часть нет (рис. 5). Но здесь тоже бывают исключения. Они относятся к тем случаям, когда между S и P отношения подчинения и S подчиняет себе P. Так, в суждении "Некоторые музыканты скрипачи" понятие скрипачей полностью входит в понятие музыкантов. Следовательно, термин, стоящий на месте предиката в таком суждении оказывается распределенным. Тем не менее, для полной достоверности выводов с такими суждениями надо полагаться на самый худший вариант: всегда и во всех случаях лишь часть предметов из объема P обладает свойством (или входит в объем) S. Таким образом, субъект и предикат частноутвердительного суждения всегда выступают нераспределенными.

У частноотрицательного суждения субъект тоже всегда не распределен по тем же причинам, что и в суждении частноутвердительном: часть предметов из объема S обязательно не обладает свойством, составляющим содержание P. С предикатом дело, однако, обстоит сложнее для понимания, так как этой категории суждений соответствует целых три разных варианта соотношений по объему между S и P (рис. 6). Поэтому понятие-предикат характеризуется очень различно с точки зрения необладания свойством, и спектр различия колеблется в крайних пределах: ни один не обладает свойством - все обладают им. Например, суждение "Некоторые альпинисты не являются горноспасателями" будет истинным как в том случае, если круг лиц, обозначаемых понятием "альпинист", совершенно не соприкасается с кругом "горноспасателей", так и при условии, что часть лиц входит и туда, и сюда, и даже если весь объем "горноспасателей" входит в объем "альпинистов"; ложным это суждение было бы только в одном случае: все альпинисты - горноспасатели.

Однако в теории умозаключений, где, прежде всего, используется распределенность терминов, как и в предыдущих видах суждений, оказывается достаточно учесть один предельный случай - все предметы из объема P не обладают свойством, о котором говорится в S. Если же окажется, что только часть предметов, охваченных понятием-предикатом, не обладает соответствующим свойством, то все правила умозаключений относительно распределенности сохраняют силу и тут тоже. Мы поэтому не придем к ошибочным выводам, если всегда будем считать распределенным понятие, образующее предикат частноотрицательного суждения, а субъект нераспределенным.

Итак, субъект всегда распределен в общих суждениях и не распределен в частных. Предикат всегда распределен в отрицательных суждениях и не распределен в утвердительных.

Логический квадрат

Благодаря количественным и качественным характеристикам даже суждения с одними и теми же субъектами и предикатами могут различаться между собой. Их называют суждениями с одинаковой материей, потому что в них речь идет об одних и тех же предметах и об тех же самых их свойствах, только в утвердительных суждениях эти свойства приписываются, а в отрицательных - отрицаются, в частных говорится о некоторых из предметов, в то время как в общих речь идет обо всех. Между суждениями этого рода устанавливаются определенные твердые соотношения по их истинностным значениям. Так, если мы возьмем общеотрицательное суждение "Ни один из киосков в этом квартале не торгует цветами" и если оно истинно, то тогда ни в коем случае не может быть истинным частноутвердительное суждение о том же - "Некоторые из киосков в этом квартале торгуют цветами". Точно так же, если бы второе было истинным, то в таком случае обязательно ложным было бы первое. Отношения между другими парами суждений с тем же субъектом и таким же предикатом выглядят иначе, но главное, что они существуют и их можно выявить.

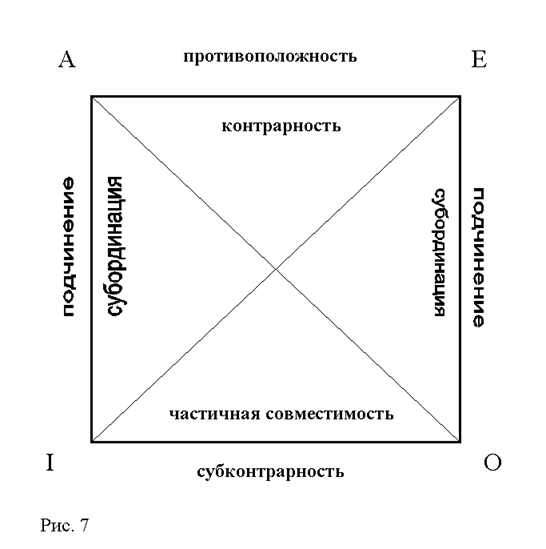
Всю систему взаимообусловленности истинностных значений суждений с одинаковой материей удобно изобразить графически с помощью так называемого логического квадрата.

Буквы на его углах символизируют различные виды суждений - A, E, I, O (см. рис. 7). А его стороны и диагонали выражают всю совокупность возможных отношений между ними. Линия AE образует отношение противоположности или, иначе, контрарности. Пары этих суждений никогда не могут быть одновременно истинными; в нашем примере истинность того и другого означала бы, что верно как утверждение о том, что все киоски в этом квартале торгуют цветами, так и о том, что ни один из них ими не торгует. Очевидно, такое невозможно. Другие же сочетания значений для пары S a P и S e P допустимы: могут быть оба ложны, и может одно быть истинным, а другое ложным. Отсюда получается правило: когда одно из противоположных суждений (S a P или S e P) истинно, то можно уверенно делать вывод, что противоположное ему истинным не является, когда же одно ложно, то никаких выводов о противоположном делать нельзя, оно может быть и тем, и другим.

Две расположенные по диагонали пары AO и EI составляют отношение противоречия или контрадикторности. Их истинностные соотношения легче всего запомнить: они не бывают ни одновременно истинными, ни одновременно ложными. Следовательно, их истинностные значения регулируются законом исключенного третьего: когда одно истинно, другое обязательно ложно и наоборот. Это значит, установив истинностное значение одного из членов пары, каким бы оно ни было, мы тем самым однозначно установили значение лежащего против него по диагонали.

Нижняя сторона квадрата IO выражает отношение частичной совместимости, или, иначе, субконтрарности. В отличие от противоположных суждений эта пара никогда не бывает одновременно ложной. В принципе можно рассматривать данное обстоятельство как следствие, обусловленное первыми двумя отношениями. В самом деле, попробуем воспользоваться теми соображениями, которые были высказаны о противоположных и противоречащих суждениях, предположив сначала, что S i P ложно, и определив значение S o P в таком случае, затем проделаем то же самое, отправляясь от того, что ложно S o P. Итак, допустим, что S i P ложно. Тогда противоречащее ему суждение S e P истинно (ибо лежащие по диагонали пары не могут быть вместе ни истинными, ни ложными); отсюда следует, что противоположное S e P суждение S a P должно быть ложным (так как из противоположных пар суждений истинным может быть только одно); но, установив ложность S a P, мы обязаны признать истинным противоречащее ему суждение S o P. Совершенно аналогично, допустив ложность S o P, мы обратным порядком придем к утверждению, что S i P в таком случае должно быть истинно. Однако при других истинностных значениях их взаимообусловленность отсутствует. Предположив, что S i P (S o P) истинно, мы сможем, правда, прийти к выводу о ложности противоречащего ему суждения S e P (S a P), но дальше рассуждение оборвется, так как при ложности одного из противоположных понятий другое может иметь любое из двух возможных значений, а значит и лежащее против него по диагонали противоречащее (и одновременно субконтрарное относительно S i P) суждение S o P может быть как истинным, так и ложным. Таким образом, получается правило в отношении субконтрарных суждений: когда одно из них ложно, другое обязательно истинно, но когда одно из них истинно, то о другом ничего сказать нельзя.

Стороны квадрата AI и EO выражают отношение подчинения или субординации. В какой-то мере его можно было бы уподобить отношению части и целого: истинность общего суждения (и утвердительного S a P, и отрицательного S e P) означает одновременно истинность частного (S i P и соответственно S o P). Если мы знаем, что все металлы электропроводны, то тем более верно говорить это о некоторых из них. Однако когда общее суждение ложно, то о частном сказать ничего нельзя; к примеру, отрицание того, что все представители данной философской школы - идеалисты, может означать как то, что их там только часть, так и то, что их там вообще нет. При движении же от частного к общему все обстоит наоборот. Лишь когда частные суждения ложны, можно делать вывод о том, что подчиняющее его суждение тоже ложно (если неверно, что часть предметов обладает (не обладает) каким-то свойством, то тогда тем более неверно сказать то же самое про все). Но если частное суждение истинно, то это оставляет нас в неведении относительно истинности или ложности общего суждения. Мы можем, например, узнать, что некоторые медведи в данной географической зоне бурые; это обстоятельство, однако, не позволит нам узнать, есть ли там еще и другие медведи или они все там бурые. Итак, основываясь на выводах об истинности общего суждения S a P и S e P, можно прийти к заключению об истинности подчиненных им суждений S i P и соответственно S o P, а от ложности частного суждения S i P и S o P можно прийти к утверждению о ложности соответствующих подчиняющих суждений S a P и S e P. При ложности же общих и истинности частных суждений никакие выводы по линии подчинения невозможны.

 

И это правило тоже можно получить в качестве следствия из отношений противоречия и противоположности. Так, если общее суждение S a P (S e P) истинно, то тогда обязательно ложно противоположное ему суждение S e P (S a P), а отсюда по линии противоречия получим, что истинно подчиненное по отношению к S a P (S e P) суждение S i P (S o P). И таким же путем, предположив ложность частных суждений, мы придем к выводу о ложности подчиняющих их общих. При других исходных значениях рассуждения не получатся из-за того, что при ложности общих суждений не допускаются выводы по линии противоположности.

Необходимо помнить о том, что теория логического квадрата построена только для неопределенно-частных суждений, когда под словом "некоторые" подразумевается "как минимум некоторые, а может быть и все". На определенно-частные, или выделяющие суждения с квантором "только некоторые", она не распространяется. Система отношений истинностных значений для этого случая не укладывается в квадрат, но зато она выглядит проще. 1) Когда истинно одно из общих суждений, то все остальные обязательно ложны; обратное тоже верно. 2) Частные суждения либо оба вместе истинны (и тогда оба общих ложны), либо оба вместе ложны (и тогда одно из общих истинно, а одно ложно).

Законы логического квадрата, как и остальные логические законы, не зависят от содержания высказываний. О чем бы ни шла речь, все отмеченные правила действуют неукоснительно. Даже если нам непонятно содержание, то все равно, опираясь на одну только логическую форму, можно сделать правильные выводы или проверить, верно или нет построено то или иное рассуждение с использованием суждений одинаковой материи.

Допустим, перед нами такой текст: "Неправильно говорить, что (1) некоторые целлы представляют собой наосы, и еще более ошибочно считать, будто (2) никакие целлы не являются наосами". Чтобы разобраться с содержанием этих мало кому известных понятий, надо сначала решить, каковы эти суждения по качеству и количеству и какое между ними отношение. Первое из них частноутвердительное - S i P, второе - общеотрицательное - S e P. Следовательно, они расположены по диагонали квадрата EI и между ними отношение противоречия (не могут быть вместе как истинными, так и ложными). Высказывание же объявляет их оба ложными. Отсюда мы можем заключить, что первое суждение может быть только определенно-частным и означает: "Только некоторые целлы есть наосы", которое объявляется ложным вместе с общеотрицательным суждением (2). Из истинностных соотношений для суждений с таким квантором следует, что частные суждения бывают ложными лишь одновременно. Тогда значит и суждение частноотрицательное тоже надо признать ложным. Истинным остается только общеутвердительное суждение S a P: "Все целлы - наосы" (то и другое представляет собой название главного помещения в древнегреческом храме, то есть эти слова синонимы).

Овладение правилами логического квадрата требует обязательной проработки всех относящихся к нему упражнений и задач. Его простые по отдельности истинностные соотношения в своей совокупности образуют довольно громоздкую и сложную систему.

Модальные суждения

До сих пор нами рассматривались суждения, в которых отмечается только отношение между предметом и его свойством. Это очень распространенная форма высказывания, поэтому она и является объектом внимания науки о законах мышления. Однако она не является единственной. Не менее, а может быть и более широкое хождение в рассуждениях и сообщениях имеют высказывания, в которых, помимо указания на связь между субъектом и предикатом, отмечается также характер этой связи: случайно принадлежит свойство субъекту или в силу необходимости, уверены мы в знании содержания высказывания или же сомневаемся, какова зависимость сделанных утверждений, скажем, от принятых в обществе ограничений и запретов, когда речь идет о нормах морали и права. Такого рода и еще многие другие дополнительные характеристики называют модальностями, а включающие их в себя суждения - модальными.

Суждения называют модальными, когда в них отмечается не только связь между субъектом и предикатом, но и дается характеристика этой связи или выражается отношение к ней автора суждения.

Слова, указывающие на характер связи, называются модальными операторами. Иногда они не высказываются прямо, но из контекста видно, что их подразумевают.

В традиционной логике наиболее полно изучены так называемые атлетические модальности (от греч. aletheia - истина, т.е. истинные, подлинные), в которых отмечается степень нерасторжимости, непреложности обязательности связи между субъектом и предикатом: иногда она может быть необходимой, иногда - только возможной, в иных же случаях суждение отмечает просто фактическую связь предмета и его свойства без дальнейших уточнений.

Так, прямоугольный ромб обязательно во всех случаях является квадратом, следовательно, суждение "Прямоугольный ромб есть квадрат" является суждением необходимости или аподиктическим; таковы же, как правило, вообще все высказывания математики и точных наук. Именно поэтому здесь чаще всего не оговаривают специально необходимый характер суждений и не вводят модальных операторов, хотя суждения являются аподиктическими. Наряду с ними имеются суждения действительности, или ассерторические; именно они рассматривались на предыдущих страницах, хотя такого названия и не употреблялось. И еще одна категория - суждения возможности, или проблематические. Они встречаются всюду, где обсуждаются перспективы предстоящих изменений и делаются предположения: "Возможно, вирус СПИДа не существовал прежде", "Возможно месторождение окажется перспективным".

Исследование атлетической модальности началось еще Аристотелем, так как его философия отводит очень большую роль категории возможности в ее противопоставлении действительности. В возможном бытии, говорит древний мыслитель, очень много специфического, например, там не действует запрет на противоречие; спектр заключенных в любой вещи возможностей колеблется с размахом от одной противоположности до другой, так что в возможности вещь является одновременно и той, и не той: медь как материал, возможно, станет шаром, но возможно и не шаром. Необходимые же связи, наоборот, избирательны, не допускают варьирования. Равносторонний треугольник всегда является равноугольным и не может быть иным. Нас, впрочем, сейчас интересует не различие этих модальных категорий, а, наоборот, связь их между собой.

Позднее в логике стали изучаться и неатлетические модальности. Обычно в каждой из них выделяются, как и в атлетической, по три категории суждений - две противоположные в каком-либо отношении и одна нейтральная. Например: "раньше", "одновременно", "позже". Мы ограничимся здесь лишь перечислением этих видов модальных суждений.

Аксиологические модальности (от греч. axios - ценный). Она объединяет суждения, в которых дается оценка тех или иных явлений: "хорошо", "безразлично", "плохо". Эту модальность иногда называют также ценностной. Высказывания вроде: "Хорошо, что университет находится в центре города", "Плохо, что цены возрастают" - относятся к этой разновидности. Само собой понятно, что в языковых выражениях в качестве операторов выступают и другие слова тоже: "полезно", "вредно", "радует", "огорчает", "мило", "отвратительно" и др. Может быть эта модальность выражена и в сравнительной форме. Тогда ее модальные операторы выглядят иначе: "лучше", "равноценно", "хуже". Учение о ценностях в философии называют аксиологией. Ее задача - вскрыть основные человеческие ценности, показать историю их возникновения, определить их возможности, перспективы и место в жизни общества.

Деонтическая модальность (от греч. deontos - нужное, должное). В ней охватываются высказывания, описывающие различного рода предписания (запреты) и, прежде всего, морально-правовые нормы, могут быть сюда отнесены медицинские, технические и прочие рекомендации, ограничения, запреты. Модальными операторами для это служат: "обязательно" ("подлежит исполнению"), "безразлично", "запрещено"; к этим трем обычно добавляют еще один дополнительный оператор - "разрешено". Существует раздел этики, называемый деонтологией, в котором рассматриваются проблемы долга и должного. Деонтологией называют также врачебную этику, предписывающую нормы поведения медицинского персонала и его взаимоотношения с пациентами.

Временные модальности. Их название говорит само за себя. Подобно аксиологическим, они распадаются на две разновидности - абсолютную и относительную. Первая из них задается операторами: "всегда", "временами", "никогда". Вторая: "раньше (чем что-либо)", "одновременно", "позже (чем что-либо)".

Эпистемические модальности (от греч. episteme - знание). Эпистемологией в западной философской литературе называют теорию познания. Поэтому данную разновидность модальных суждений можно было бы называть еще и теоретико-познавательной. Здесь отмечается степень изученности явлений, о которых говорится в высказываниях. В зависимости от того, идет ли речь об уровне знания или об уровне убежденности, различают две разновидности эпистемической модальности. Одна из них выражается операторами: "доказуемо" ("верифицируемо"), "неразрешимо", "опровержимо" ("фальсифицируемо"). Для другой операторами служат: "отстаивает" ("убежден"), "сомневается", "отвергает".

Глава 4. Умозаключение

Из суждений составляется более сложная и важная в теоретическом отношении форма логического мышления - умозаключение. Иногда к ним прилагают название "силлогизм", хотя, строго говоря, силлогизм - только одна из разновидностей умозаключения, правда, наисложнейшая и, пожалуй, самая распространенная. С помощью умозаключения мысли, выражаемые через суждения, связываются между собой, образуя новую мысль, которую можно рассматривать результатом их сцепления, взаимодействия. Возьмем для наглядности такое рассуждение:

 

Если число 64 делится на 3 и на 4, то оно делится на 12.

Число 64 не делится на 12.

Следовательно, число 64 не делится на 3 или на 4.

 

Это так называемая усложненная контрапозиция. При такой схеме рассуждения из высказываний, составляющих первые две строчки, с необходимостью вытекает третье (третья строчка). Мы могли бы взять и какие-то другие явления, связанные подобным же образом, например: если дует сильный ветер и падает снег, то значит на улице пурга; но пурги нет; следовательно, на улице не падает снег или нет ветра.

Умозаключение - это форма мышления, позволяющая из одного или нескольких суждений, называемых посылками, извлекать с помощью правил логики новое суждение - заключение.

Когда исходные высказывания в правильно построенном умозаключении истинны, то и вывод его тоже обязательно будет истинным суждением.

Понятия и суждения как формы мышления формируются большей частью за пределами логики, которая берет их уже готовыми. Умозаключение же формируется из суждений именно по логическим правилам.

На стадии умозаключения о вещах можно рассуждать, не обращаясь к ним самим. Достаточно иметь о них несколько верных высказываний. По этой причине, опираясь на правила умозаключения, наука получает возможность рассуждать о природных явлениях теоретически, постигать те их стороны, которые скрыты за внешней, доступной наблюдению поверхностью, проникать в недоступные природные глубины, обращаться мыслью в такие запредельные дали, которые можно изучать лишь умозрительно. Палеонтологам иной раз хватает одной кости для воссоздания всего облика давно вымерших животных. Сходные достижения имеются во всех других науках. Например, Демокрит догадался о существовании атомов, наблюдая, как истираются со временем каменные ступени храма. Много великих и малых тайн природы разгадано благодаря тонким и сложным рассуждениям. Цепь умозаключений выстраивается порой в целые обширные теории.

Всю совокупность известных логике умозаключений принято классифицировать по двум основаниям: во-первых, по числу посылок, во-вторых, по направлению движения мысли. Что касается числа посылок, то с этой точки зрения весь их массив распадается на две неравновесные части, те, у которых посылка всего одна, и остальные. Первые называются непосредственными умозаключениями. Они относятся к наиболее простым их разновидностям. В них происходит простая смена логической формы того или иного высказывания, содержание же остается неизменным. Помимо самой посылки в таком преобразовании участвуют также и логические законы мышления. Во вторых, опосредствованных, умозаключениях посылок более одной, они сложнее и многообразнее первых.

По другому основанию умозаключения делят на дедуктивные, в которых мышление движется от общих положений к частным выводам, индуктивные, делающие обобщения из частных наблюдений, и такие, у которых уровень общности посылок и заключения одинаков; к ним, прежде всего, относится аналогия и некоторые суждения с отношениями; иногда последнюю группу объединяют под названием традуктивные умозаключения.