
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Генеральная совокупность и выборка
Согласно закону больших чисел, статистическая устойчивость результатов наблюдений имеет место при достаточно большом числе измерений. Однако на практике обычно имеют дело лишь с небольшим числом наблюдений, т. к. рассмотрение всей совокупности объектов во многих случаях невозможно и нецелесообразно. Например, анализ среднего дохода населения крупного административного центра предполагает наличие достоверной информации о каждом жителе города в конкретный момент времени. Получение такой информации весьма затруднительно. Проверка качества многих промышленных товаров связана с проведением механических и климатических испытаний, воздействием химических факторов, электрических и магнитных полей, что приводит к полной или частичной утрате исследуемых объектов [11,16]. Естественно, что характеристики СВ, определенные по малому числу наблюдений, могут не совпадать с теми же величинами, вычисленными по большому (в пределе – бесконечно большому) числу наблюдений, выполненных в тех же условиях. Поэтому, чтобы оценить соответствующие различия, в математической статистике вводят понятие абстрактной генеральной совокупности, представляющей собой множество всех теоретически возможных значений СВ, реализуемых в данных условиях, и выборки (выборочной совокупности), состоящей из ограниченного числа значений (наблюдений) и представляющей собой часть генеральной совокупности, отобранную для изучения. В соответствии с этим различают выборочные характеристики СВ, найденные по ограниченному числу наблюдений и зависящие от этого числа, и соответствующие характеристики генеральной совокупности, не зависящие от числа наблюдений. При этом выборочные характеристики рассматриваются как оценки соответствующих генеральных характеристик. Основная задача выборочного метода в математической статистике состоит в исследовании свойств выборки и обобщении этих свойств с наибольшей надежностью на генеральную совокупность. Согласно закону больших чисел можно утверждать, что выборка будет репрезентативной, т. е. достаточно полно отражать пропорции генеральной совокупности, если отбор объектов для исследования будет носить случайный характер.
Способы представления статистических данных
И выборочные характеристики
При анализе какого-либо экономического показателя Х в фиксированный момент времени (либо без учета фактора времени) наблюдаемые его выборочные значения х 1, х 2, …, хn обычно упорядочивают по возрастанию. Разность между максимальным и минимальным значением СВ Х называется размахом выборки. Пусть количество различных значений в выборке равно k (k £ n). Значения xi, i = 1, 2, …, k называются вариантами выборки. При этом х 1 < x 2 < … < xk. Если значение хi встретилось в выборке ni раз, то число ni называется абсолютной частотой значения хi, а величина
Таблица 1.1
При этом По вариационному ряду можно построить эмпирическую функцию распределения для СВ Х. Эмпирической (выборочной) функцией распределения Fn (x) будем называть относительную частоту (статистическую вероятность) появления события, заключающегося в том, что СВ Х примет значение, меньше указанного х, т. е.: Fn (x) = ω(X < x). (1.29) По определению Fn (x) обладает следующими основными свойствами: 1. 0 £ Fn (х) £ 1. 2. Fn (x) = 0 при Х £ х 1; Fn (x) = 1 при X > xk. Эмпирическая функция распределения Fn (x) является оценкой функции F (x) = P (X < x), которую в этом случае следует называть теоретической функцией распределения. Пример 1.2. Анализируется прибыль Х (%) предприятий отрасли. Обследованы n = 100 предприятий, данные по которым занесены в следующий вариационный ряд [11]:
Необходимо определить эмпирическую функцию распределения Fn (x) и построить ее график.
Рис. 1.7.
При большом объеме выборки ее элементы могут быть сгруппированы в интервальный вариационный ряд. Для этого n наблюдаемых значений выборки х 1, х 2, …, хn разбивают на k непересекающихся интервалов равной ширины h (h – шаг разбиения). Пусть ni – количество наблюдаемых значений СВ Х, попадающих в i -й интервал;
Таблица 1.2
Интервальный вариационный ряд наглядно может быть представлен в виде гистограммы – графика, где по оси абсцисс откладываются интервалы, на каждом из которых строятся прямоугольники с высотой и площадью, пропорциональной относительной частоте попадания СВ Х в данный интервал. На i -м интервале строится прямоугольник высотой Задача (гипотеза) о соответствии теоретического и статистического распределения обычно рассматривается с помощью статистического критерия Пирсона [16], основанного на распределении Поскольку на практике обычно работают с выборкой, нас будут интересовать выборочные числовые характеристики, которые являются оценками соответствующих генеральных характеристик. Если в формуле для математического ожидания дискретной СВ (1.4) положить равными вероятности каждого исхода pi = 1/ n, то получим выборочное среднее арифметическое наблюдаемых значений выборки для СВ Х:
При задании выборки в виде вариационного ряда
Соответственно, для выборочной дисперсии получим формулы:
или (1.32)
Зачастую для вычисления Dв (Х) удобно использовать выражение:
Выборочное среднее квадратическое отклонение определяется как
При задании выборки в виде интервального вариационного ряда в формулах (1.31), (1.32) вместо xi рассматривается среднее значение i -го интервала Выборочный коэффициент вариации Vв будет определяться процентным отношением выборочного среднего квадратического отклонения к выборочному среднему:
Коэффициент вариации – безразмерная характеристика, удобная для сравнения величин рассеивания двух выборок, имеющих различные размерности. Наиболее распространенными характеристиками взаимосвязи двух СВ являются меры их линейной связи – ковариация и коэффициент корреляции (см. раздел 1.4). Их оценками являются выборочная ковариация Covв (X, Y) и выборочный коэффициент корреляции rxy.
Здесь Известно, что если величины X и Y независимы, то выборочный коэффициент корреляции равен нулю; если rxy равен Для нахождения выборочных ковариации и коэффициента корреляции необходимо иметь выборку объема n из двумерной генеральной совокупности (Х, Y), где рассматриваются пары значений xi, yi (i = 1, 2, …, n) в ряду наблюдений. Выборочные оценки числовых характеристик генеральной совокупности обладают теми же основными свойствами, что и их теоретические прототипы.
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 336; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.255.134 (0.013 с.) |
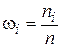 – относительной частотой значения хi. Тогда наблюдаемые выборочные значения можно представить в виде вариационного (статистического) ряда (табл. 1.1).
– относительной частотой значения хi. Тогда наблюдаемые выборочные значения можно представить в виде вариационного (статистического) ряда (табл. 1.1).

 …
… 
 ,
,  .
.



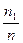


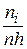 . На основании гистограммы обычно выдвигают предположение о виде закона распределения исследуемой СВ Х.
. На основании гистограммы обычно выдвигают предположение о виде закона распределения исследуемой СВ Х. (Приложение 6).
(Приложение 6). . (1.30)
. (1.30) . (1.31)
. (1.31)
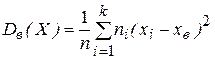 .
. . (1.33)
. (1.33) . (1.34)
. (1.34) .
. . (1.35)
. (1.35) , (1.36)
, (1.36)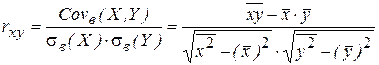 . (1.37)
. (1.37) .
. , то Y и X связаны линейной функциональной зависимостью [16].
, то Y и X связаны линейной функциональной зависимостью [16].


