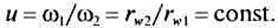Основы теории зубчатого зацепления

Профили зубьев пары колес должны быть сопряженными, т. е. заданному профилю зуба одного колеса должен соответствовать вполне определенный профиль зуба другого колеса. Чтобы обеспечить посто­янство передаточного числа, профили зубьев нужно очертить такими кривыми, которые удовлетворяли бы требованиям основной теоремы зацепления.

Основная теорема зацепления. Для доказательства теоремы рассмот­рим пару сопряженных зубьев в зацеплении (рис. 11.6). Профили зубьев шестерни и колеса касаются в точке S, называемой точкой зацепления. Центры вращения О, и 0₂ расположены на неизменном расстоянии а„ друг от друга. Зуб шестерни, вращаясь с угловой скоростью со,, ока­зывает силовое действие на зуб колеса, сообщая последнему угловую скорость ω₂. Проведем через точку S общую для обоих профилей ка­сательную ТТ и нормаль NN. Окружные скорости точки S относитель­но центров вращения О₁ и 0₂

Разложим v₁ и v₂ на составляющие v\ и v'₂ по направлению нормали NN и составляющие v"₁ и v"₂ по направлению касательной ТТ. Для обеспечения постоянного касания профилей необходимо соблю­дение условия V₁ = v₂, в противном случае при v, < v₂ зуб шестер­ни отстанет от зуба колеса, а при v\ > v'₂ произойдет врезание зубь­ев. Опустим из центров О₁ и 0₂ перпендикуляры 0₁В и 0₂С на нор­маль NN.

Нормаль NN пересекает линию центров 0₁ 0₂ в точке П, называ­емой полюсом зацепления. Из подобия треугольников 0₂ПС и 0,ПΒ

0₁C/O_lB=0₁n/O_ln = r_w2/r_wl. Сравнивая отношения (11.1) и (11.2), получаем

Таким образом, основная теорема зацепления формулируется так: для обеспечения постоянного передаточного числа зубчатых колес профи­ли их зубьев должны быть очерчены по кривым, у которых общая нормаль NN, проведенная через точку касания профилей, делит расстояние между центрами 0₁ 0₂ на части, обратно пропорциональные угловым скоростям.

Полюс зацепления П сохраняет неизменное положение на линии центров 0₁ 0₂, поэтому радиусы r_w1 и r_w2 также неизменны.

Окружности радиусов r_w1 и r_w2 называют начальными. При вращении зубчатых колес начальные окружности перекатываются друг по другу без

скольжения, о чем свидетельствует равенство окружных скоростей со,г_ю, = aty^, полученное из формулы (11.3).

Из множества кривых, удовлетворяющих требованиям основной теоремы зацепления, практическое применение в современном маши­ностроении получила эвольвента окружности, которая:

а) позволяет сравнительно просто и точно получить профиль зуба
в процессе нарезания;

б) без нарушения правильности зацепления допускает некоторое
изменение межосевого расстояния а_w (это изменение может возник­
нуть в результате неточностей изготовления и сборки, деформаций
деталей передачи при работе).

Эвольвента окружности (рис. 11.7). Эвольвентой окружности называют кри­вую, которую описывает точка S пря­мой NN, перекатываемой без скольже­ния по окружности радиуса r_ь. Эту ок­ружность называют эволютой или основ­ной окружностью, а перекатываемую прямую NN— производящей прямой.

Характер эвольвентного зубчатого зацепления определяется свойствами эвольвенты (см. рис. 11.7):

1. Производящая прямая NN являет­
ся одновременно касательной к основ- ^Рис- "-⁷- ^Схема образования

эвольвенты нои окружности и нормалью ко всем

производимым ею эвольвентам.

2. Две эвольвенты одной и той же основной окружности эквиди-станты (т. е. расстояние между эвольвентами в направлении нормали везде одинаковое).

3. С увеличением радиуса r_h основной окружности эвольвента ста­новится более пологой и при r_ь -> °° обращается в прямую.

4. Радиус кривизны эвольвенты в точке S₂ равен длине дуги S₀B основной окружности. Центр кривизны эвольвенты в данной точке находится на основной окружности.

Образование эвольвентного зацепления

Пусть заданы межосевое расстояние a_w и передаточное число и зубчатой передачи (рис. 11.8). При известных a„ = r_wl + r_w2 и u = r_w2/r_wl определим радиусы начальных окружностей r_vl = a_w/(u+l), r_vl-ur_M и отметим на линии центров О_х0₂ положение полюса зацепления П.

Из центра О, опишем некоторым радиусом г_м основную окруж­ность и, произведя ее развертку, получим эвольвентный профиль А₁ зуба шестерни. На основании основной теоремы зацепления и первого свойства эвольвенты проведем через полюс П нормаль NN, которая определит точку зацепления S сопряженных профилей. Опустим из центра 0₂ перпендикуляр 0₂С на нормаль NN и радиусом r_h2-0₂C

и конце зацепления

опишем основную окружность, развертка которой даст эвольвентный профиль А₂ зуба колеса. Построенные профили — сопряженные, так как, касаясь в точке S, они имеют общую нормаль NN. Эта нормаль каса­ется обеих основных окружностей и является производящей прямой эвольвент обоих профилей.

При вращении колес точка зацепления S эвольвентных профилей перемещается по общей нормали NN (рис. 11.9) — геометрическому месту точек зацепления сопряженных профилей, называемому линией зацепления. Линия зацепления NN является одновременно линией дав­ления, так как сила давления профиля зуба шестерни на профиль зуба колеса (в предположении отсутствия сил трения) действует по общей нормали NN к обоим профилям.

Угол oc_w, образованный линией зацепления NN (см. рис. 11.8) и общей касательной ТТ к начальным окружностям, называют углом зацепления.

Из формулы (11.3) следует

т. е. отношение угловых скоростей двух сопряженных эвольвентных про­филей обратно пропорционально радиусам основных окружностей и не зависит от расстояния a_w между центрами этих окружностей.

 

 

Рис. 11.10. Схема к доказательству независимости и от о„

Независимость передаточного числа и от изменения межосевого расстояния а„ можно проследить на следующем примере.

Пусть на рис. 11.10, а изображено зацепление при заданном a_w и передаточном числе и. Изменим межосевое расстояние этого зацепле­ния до a_w + Aa_w (рис. 11.10,6). Сопоставляя рисунки, видим, что в за­цеплении с расстоянием a_w + Aa„ возникли новые начальные окружно­сти с радиусами r'_п1 и r'_w2- Радиусы основных окружностей не измени­лись, так как не изменились профили зубьев, они остались очерчен­ными теми же эвольвентами. Из подобия треугольников 0₂СП и 0,6П (рис. 11.10,6)

Таким образом, правильность эвольвентного зацепления не наруша­ется при изменении межосевого расстояния а„. Это свойство является важным преимуществом эвольвентного зацепления перед циклоидаль­ным, весьма чувствительным к изменению расстояния а„.

Образование цилиндрического зубчатого колеса

Реальные зубчатые колеса характеризует ширина зубчатого венца (обода). В зацеплении участвуют не профили, а поверхности зубьев, следовательно, касанию плоских профилей в точке соответствует ка­сание поверхностей по линии контакта. Основным окружностям колес соответствуют основные цилиндры колес, начальным окружностям — начальные цилиндры, окружностям вершин — цилиндры вершин, окружностям впадин — цилиндры впадин.

На рис. 11.11 изображен основной цилиндр радиуса г_ь и каса­тельная к нему плоскость N, на поверхности которой на определен­ных расстояниях нанесены прямые ВС, DF,..., параллельные обра-

 

 

Рис. 11.11. Образование цилиндрического зубчатого

зующей цилиндра. При перекатывании спра­ва налево плоскости Л" прямая ВС описыва­ет в пространстве правую эвольвентную по­верхность зуба. Левую поверхность образует прямая DF при перекатывании плоскости N в обратном направлении. Образовав анало­гичным способом боковые поверхности ос­тальных зубьев и ограничив их высоту ци­линдрами вершин и впадин, получим венец эвольвентного цилиндрического прямозубо­го колеса.