Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зведення мережевої транспортної задачі до матричної форми ⇐ ПредыдущаяСтр 4 из 4
Методом Ордена
Рис. 4.3. Розв'язання мережевої ТЗ без обмежень на пропускні здатності за допомогою Excel-таблиці Другий спосіб – спосіб Вагнера Ш.М. Він зручніший для мереж з обмеженнями пропускної здатності. Така мережа зображена на рис. 4.2, де представлений також і оптимальний план перевезень. У табл. 4.2 показано приведення цієї мережі до матричної форми. Таблиця 4.2 Зведення мережевої задачі до матричної форми методом Вагнера
Для дуг тут відведені рядки, а для вершин стовпці. У верхньому лівому куті клітинки таблиці зазначена вартість перевезення по дузі. Там, де в клітинках немає цифр, передбачається їхнє блокування більшим числом М. числами (у табл. 4.2 це незаповнені клітинки).
Обсяг виробництва дорівнює пропускній здатності дуги, тобто Обсяг споживання для виробляючих вершин мережі визначають за формулою:
для вершин, які споживають вантаж за формулою:
для транзитних вершин за формулою:
Таким чином, для вершини 1 обсяг споживання дорівнює 1+5+2–7=1, для вершини 7 –7+100+6=113, а для вершини 2 –1+5+3=9. У табл. 4.2 також показано остаточний результат розв’язання задачі – оптимальний план перевезень вантажу поданий у вигляді виділених курсивом значень, що відповідає потокам на рис. 4.2, а на рис. 4.4 – результат розв'язання за допомогою Excel-таблиці У клітинках з вартістю, рівною нулю, потік є доповненням до пропускної здатності, тобто фіктивним.
Рис. 4.4. Розв'язання мережевої ТЗ з обмеженнями на пропускні здатності за допомогою Excel-таблиці
ЛАБОРАТОРНА РОБОТА № 5. РОЗВ'ЯЗАННЯ СІТЬОВИХ ТРАНСПОРТНИХ ЗАДАЧ. ЗадачІ про найкоротший шлях ТА максимальний потік НА мережі ЗАВДАННЯ ДО ЛАБОРАТОРНОЇ РОБОТИ
1. Знайти найкоротший шлях на транспортній мережі (див. рис. 5.1) за допомогою Excel-таблиці (добавив додатковий транспортний вузол з наведеної нижче карти), одержати оптимальний план перевезень за допомогою “EXCEL -2003”. Проаналізувати результати. 2. Знайти максимальний потік на транспортній мережі (див. рис. 5.1) за допомогою Excel-таблиці (добавив додатковий транспортний вузол з наведеної нижче карти), одержати оптимальний план перевезень за допомогою “EXCEL -2003”. Проаналізувати результати. ВАРІАНТИ ЗАВДАНЬ
Додати до структури транспортної мережі (рис. 5.1) транспортний вузол з наведеної нижче карти.
МЕТОДИЧНІ ВКАЗІВКИ ДО ВИКОНАННЯ ЛАБОРАТОРНОЇ РОБОТИ Класичними задачами на графах є задачі про побудову найкоротших шляхів та їх сукупностей у вигляді відповідних дерев чи контурів. Однією з таких задач є пошук найкоротшого шляху між двома заданими вузлами: s (джерелом) і t (стоком). Розглянемо розв'язання цієї задачі на конкретному прикладі, який узятий з електронного атласу України:
Задана сітка у вигляді змішаного зваженого графа з 9 вузлами і 13 дугами, початкові дані мають наступний вигляд у Excel -таблиці(див. рис. 5.1). Треба визначити найкоротший шлях від вузла –джерела міста Київа до вузла-стоку міста Суми в следующей математической постановке: - знайти вектор Х = (х1, х2, … х13), де елемент хi = 1, якщо відповідна дуга належить найкоротшому шляху, і 0 у противному випадку; і – порядковий номер дуги (і = 1, 2,..., 13); - щоб загальна довжина шляху - за умови збереження балансу потоків для кожного j -го вузла (j = 1, 2,..., 9): Fвих (xi) - Fвх (xi) = 0, де Fвих (xi), Fвх (xi) – сума потоків на вході та виході кожного j -го вузла; для вузла-джерела Fвих (xi) - Fвх (xi) = 1; для вузла –стока Fвих (xi) - Fвх (xi) = -1; - при всіх xi ≥ 0.
Рис. 5.1. Топологія сітьової транспортної задачі Для цього в Excel -таблиці (далі просто таблиці) для всіх дуг визначити діапазон для невідомих Х (Дуга) і обчислити значення цільової функції за формулою = СУММПРОИЗВ(Дуга; Довжина), а для всіх вузлів обчислити суми вхідних (Вхід) і вихідних (Вихід) потоків, їх алгебраїчну суму (Вихід-Вхід), задати колонку правих частин обмежень (Обмеження). Для обчислення потоку у вузлах використовується функція обчислення суми величин, координати яких задовольняють визначеній умові (тобто, якщо певні величини належать відповідній множині). В Excel таку процедуру виконує функція СУММЕСЛИ(аргументи). Наприклад, сума вхідних потоків вузла визначається за формулою = СУММЕСЛИ(всі кінці дуг; вузол; потоки), тобто, підсумовуються потоки по тих дугах, кінці яких співпадають з поточним вузлом. За формулою = СУММЕСЛИ(всі початки дуг; вузол; потоки) підсумовуються вихідні потоки. На рис. 5.2 показане розв'язання поставленої задачи за допомогою команди Пошук рішення в середовищі Excel - програми, з котрого видно, що ветор Х = (0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1), а це, у свою чергу означає, що найкоротший шлях з міста Києва в місто Суми пройде послідовно через міста Березань, Пирятин і Гадач і складе 378 км.
Рис. 5.2. Розв'язання задачі про найкоротший шлях на мережі Задача про максимальний потік у мережі. Задача про максимальний потік на мережі – класична потокова задача, де параметром кожної дуги змішано-орієнтованої мережі є її максимальна пропускна здатність. Ця задача та її варіанти знаходять свое застосування при дослідженні потоків (величин і напрямків) транспортних мереж різного типу (шляхи, трубопроводи, канали зв’язку) для руху пасажирів, транспортних засобів, газу, інформації тощо. Результат рішения цієї задачі вказує величину максимального загального потоку, який може пропустити вся мережа, потоки та їх напрямки по окремих дугах. Розглянемо розв’язання задачі про максимальний потік у мережі на конкретному прикладі, який також узятий з електронного атласу України у вигляді зваженого графа з 6 вузлами і 11 дугами (топологія розглянутого графа збігається з топологією графа на рис. 5.1, де максимальний потік знаходився методом дерев), початкові дані мають наступний вигляд у Excel -таблиці (див. рис. 5.3).
Рис. 5.3. Розв'язання задачі про максимальний потік у сітці Задана сітка зі смішаною орієнтацією дуг і з відповідними пропускними здатностями дуг. Потік витікає з вузла-джерела міста Прилуки, потім розтікається по всіх дугах і втікає у вузол-стік місто Суми. Необхідно знайти такі потоки по дугах, щоб величина потоку з джерела у стік була максимальною. Змішану щодо орієнтації сітку перетворюємо в повністю орієнтовану заміною кожної неорієнтованої дуги парою напрвлених назустрич дуг і представимо початкові дані у вигляді двох таблиць (для дуг та вузлів). Загальний потік у сітці визначається сумою двох потоків: - з джерела: (Прилуки, Бобровиця) + (Прилуки, Ніжин) + (Прилуки, Ромни), тобто Fвих (1) = х12 + х13 + х15; - у стік: (Ніжин, Суми) + (Пирятин, Суми) + (Ромни, Суми), тобто Fвх (6) = х36 + х46 + х56, яки і визначають значення максимального потоку на мережі (значення цільової функції). Обмеження на потоки по дугах мають наступний вигляд: - величина потоку ≤ пропускна здатність (хij ≤ cij); - потік з джерела = потік у стік, тобто Fвих (1) = Fвх (6); - потенціали проміжних вузлів (2, 3, 4, 5) рівні 0, тобто Fвих (х) = Fвх (х). На рис. 5.4 представлене графічне представлення результату рішення задачі про максимальний потік на мережі. Напрямок руху потоку показано у вигляді стрілок, а величини потоків на окремих дугах представлені у вигляді знаменника дробі (при цьому чисельник дробі є ні що інше, як величина пропускної здатності відповідної дуги).
Рис. 5.4. Графічне представлення максимального потоку на мережі
ЛАБОРАТОРНА РОБОТА № 6. РОЗВ’ЯЗАННЯ МережевОЇ транспортнОЇ задачІ.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 269; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.192.3 (0.032 с.) |

 . Для дуг, де пропускна здатність не обмежена, зокрема для дуг 3–7 і 7–3, вона відповідатиме (у нашому прикладі) числу – 100.
. Для дуг, де пропускна здатність не обмежена, зокрема для дуг 3–7 і 7–3, вона відповідатиме (у нашому прикладі) числу – 100. , (4.1)
, (4.1)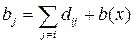 , (4.2)
, (4.2) . (4.3)
. (4.3)

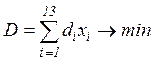 , де di – довжина і -ої дуги;
, де di – довжина і -ої дуги;