Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ:  Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия ЭкологияТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Завдання до лабораторної роботиСтр 1 из 4Следующая ⇒
ЗАВДАННЯ ДО ЛАБОРАТОРНОЇ РОБОТИ
Розподілити N кількість робітників Аi по N видів робіт Bj ВАРІАНТИ ЗАВДАНЬ Номер завдання дорівнює послідній цифрі у номері залікової книжки студента.
МЕТОДИЧНІ ВКАЗІВКИ ДО ВИКОНАННЯ ЛАБОРАТОРНОЇ РОБОТИ Виходячи з умови задачі можна припустити, що числами в таблиці можуть бути, приміром, продуктивність i- го робітника при виконанні їм j- ой роботи. Тому цілком природним результатом рішення цієї задачі буде одержання максимальної сумарної продуктивності після виконання кожним робітником однієї з наведених робіт. (Під продуктивністю в цьому випадку можна вважати кількість одиниць продукції, що буде випущена кожним робітником за певну одиницю часу).
Спробуємо звести цю задачу до задачі цілочисельного лінійного програмування. Для цього представимо закріплення (призначення) кожного з n робітників на одну з наявних n робіт у вигляді наступної матриці
у котрій
А тому що кожний із працівників може виконувати тільки одну роботу, а кожна робота повинна виконуватися тільки одним робітником, що означає наявність у кожному рядку й у кожному стовпці матриці Y тільки однієї одиниці. Математично це запишеться у наступному виді
Виходячи з того, що всі yij можуть приймати значення 0 або 1, можна замінити вимогою, щоб всі yij були ненегативними цілими числами
Як бачимо, закріплення (призначення) кожного з n робітників на одну з наявних n робіт можна представити у вигляді матриці Y, елементи котрої yij задовольняють вищенаведеним співвідношенням. При этом суммарная производительность всех работников найдётся по формуле
де dij – продуктивність i- го робітника при виконанні їм j- ой роботи. У такий спосіб знаходження оптимального плану закріплення всіх робітників за роботами, що є в наявності зводиться до знаходження значень змінних yij, що задовольняють наведеним вище лінійним рівностям і нерівностям, умові цілочисельності й обертаючих у максимум лінійну форму L, тобто до рішення задачі цілого чисельного лінійного програмування. Нижче наведений результат розв'язання поставленої задачі за допомогою функції “Пошук рішення” табличного процесора EXCEL (рис. 1.1). У верхній частині рис. 1.1 наведена таблиця з вихідними даними, а в нижній його частині – сам результат рішення, що призначає: - першого працівника А1 для виконання першої роботи В1; - другого працівника А2 для виконання другої роботи В2; - третього працівника А3 для виконання п'ятої роботи В5;
- четвертого працівника А4 для виконання третьої роботи В3; - п'ятого працівника А5 для виконання четвертої роботи В4. Сумарна максимальна продуктивність всіх робітників при такому закріпленні за роботами становить 32 одиниці часу (див. клітку цільової функції В32). При цьому клітки з Н11 по Н15 містять суми розташованих ліворуч п'яти кліток, а клітки із В16 по G16 - суми розташованих вище п'яти кліток і в клітках із В17 по G17 полічені продуктивності всіх робіт після їх найбільш успішного закріплення за працівниками. Зокрема для клітки В17 це опишеться наступною формулою - В3*В11+В4*В12+В5*В13+В6*В14+В7*В15. Клітка із цільовою функцією В32 містить суму п'яти кліток розташованих праворуч від її, що означає сумарну оптимальну продуктивність всіх п'яти робітників після виконання ними відповідних робіт.
Рис. 1.1. Результат розв'язання поставленої задачі за допомогою функції “Пошук рішення” табличного процесора EXCEL На рис. 1.2 наведене діалогове вікно функції “Пошук рішення” табличного процесора EXCEL, де описані: - цільова клітка В17; - напрямок оптимізації - максимізація; - діапазон змінюваних кліток - В11:G15; - обмеження задачі, які задані у вигляді однієї нерівності (В11:G15 >= 0) і двох рівностей (C8:G8 = C16:G16 і Н3:Н7 = Н11:Н15).
Рис. 1.2. Діалогове вікно функції “Пошук рішення” табличного процесора EXCEL ЛАБОРАТОРНА РОБОТА № 2. РОЗВ’ЯЗАННЯ ЗАДАЧІ ПРО КОМІВОЯЖЕРА ВАРІАНТИ ЗАВДАНЬ Номер завдання дорівнює порядковому номеру студента у журналі академічної групи.
ЛАБОРАТОРНОЇ РОБОТИ Розв'язання задачі Представимо таблицю з вихідними даними у наступному вигляді матриці відстаней (МВ):
Для одержання оцінки знизу довжин безлічі всіх гамільтонових контурів (ГК) скористаємося тим, що в кожний ГК входить тільки по одному елементі з кожного рядка й з кожного стовпця МВ. Тому якщо елементи будь-якого рядка або будь-якого стовпця зменшити на яке-небудь число, то на це ж число зменшаться довжини всіх ГК. На цій властивості заснований метод приведення МР. (ГК це замкнутий елементарний шлях, тобто елементарний контур, що проходить через всі населені пункти розглянутої задачі). Приведення матриці може провадитися по рядках і по стовпцях. Приведення МВ по рядках укладається в тім, що з елементів кожного рядка i віднімається найменший елемент цього рядка, позначуваний hi. При цьому довжини всіх ГК зменшаться на суму віднятих з кожного рядка чисел, тобто на величину
Одержувана після приведення МВ дана у вигляді наступної таблиці:
Метод приведення МВ будемо застосовувати й далі для одержання оцінок знизу різних підмножин множини ГК. Розглянемо тепер спосіб розбивки множини ГК на підмножини. Візьмемо деяку дугу (i, j). До першої підмножини віднесемо всі ГК, у які ця дуга входить. Позначимо цю підмножину [(i, j)]. До другої підмножини віднесемо всі ГК, у які дуга (i, j) не входить. Цю підмножину позначимо МВ для підмножини [(i, j)] легко одержати, якщо врахувати, що включення дуги (i, j) у ГК виключає можливість включення інших дуг, що коштують в i-ом рядку або j-ом стовпці. Отже, МВ для підмножини [(i, j)] виходить із первісної таблиці викреслюванням i-ого рядка й j-ого стовпця. Для того, щоб одержати МВ для підмножини Тепер виникає питання: яку дугу покласти в основу розбивки множіни ГК на відповідні підмножини? Якщо як дуга (i, j) взяти таку, у якої в наведеній таблиці Але таких дуг трохи. Яку ж з них вибрати? Очевидно, ту, для якої збільшення оцінки для підмножини Позначимо збільшення оцінки підмножини Знову звернемося до нашого приклада. Для наведеної МВ значення
Найбільше збільшення оцінки для групи
При одержанні подібних матриць потрібно строго стежити за тим, щоб не могло вийти контурів, що не є ГК. Оскільки дуга (2, 3) уже уведена в намічений ГК, то в останній таблиці потрібно накласти заборона на дугу (3, 2), відзначивши еее хрестиком, тому що дуга (3, 2) разом з дугою (2, 3) утворить контур.
Нижче представлена наведена МВ зі збільшенням оцінки
Для неї величини
Найбільше збільшення оцінки для групи Отже, подальші перетворення не доречні й отриманий ГК є оптимальним з величиною шляху 17: 2 4 6 5
Спробуємо звести цю задачу до задачі цілочисельного лінійного програмування. Для цього сукупність дуг ГК можна описати у вигляді наступної матриці
у котрій
А тому що кожна вершина зустрічається в ГК лише один раз, що означає наявність у кожному рядку й у кожному стовпці матриці Y тільки однієї одиниці. Математично це запишеться у наступному виді
Виходячи з того, що всі yij можуть приймати значення 0 або 1, можна замінити вимогою, щоб всі yij були ненегативними цілими числами
Як бачимо, кожний ГК можна представити у вигляді матриці Y, елементи котрої yij задовольняють вищенаведеним співвідношенням. При этом длина ГК, яка дорівнює суме довжин складових його дуг, найдётся по формуле
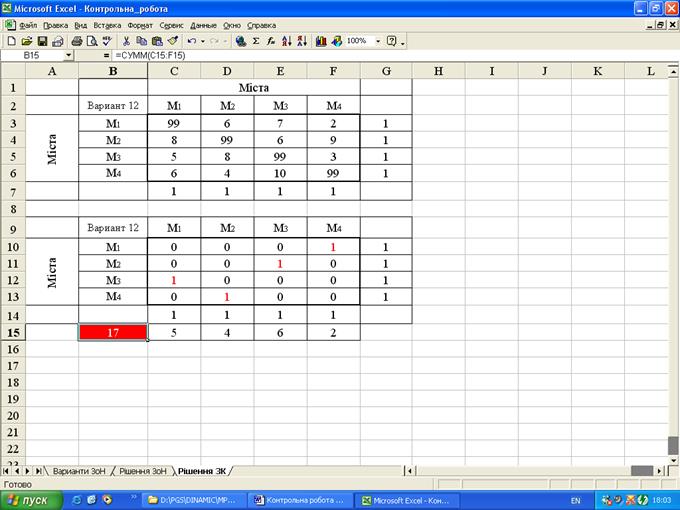
де dij – величина відстані від i- го населеного пункту до j- ого. У такий спосіб знаходження оптимального ГК мінімальної довжинизводиться до знаходження значень змінних yij, що задовольняють наведеним вище лінійним рівностям і нерівностям, умові цілочисельності й обертаючих у максимум лінійну форму L, тобто до рішення задачі цілого чисельного лінійного програмування. Нижче наведений результат розв'язання поставленої задачі за допомогою функції “Пошук рішення” табличного процесора EXCEL (рис. 2.1). У верхній частині рис. 2.1 наведена таблиця з вихідними даними, а в нижній його частині – сам результат рішення, що означає послідовне переміщення комівояжера: - з першого міста у четверте (клітка F10); - потім з четвертого міста у друге (клітка D13); - потім з другого міста у третє (клітка E11); - і в конце з третього міста у перше (клітка C12). Сумарна мінімальна довжина оптимального ГК становить 17 одиниць відстані (див. клітку цільової функції В15). При цьому клітки з G10 по G13 містять суми розташованих ліворуч чотирьох кліток, а клітки із С14 по F14 - суми розташованих вище чотирьох кліток і в клітках із С15 по F15 полічені мінімальні відстані дуг ГК. Зокрема для клітки С15 це опишеться наступною формулою - С3*С10+С4*С11+С5*С12+С6*С13. Клітка із цільовою функцією В15 містить суму чотирьох кліток розташованих праворуч від її, що означає сумарну мінімальну довжину ГК.
Рис. 2.1. Результат розв'язання поставленої задачі за допомогою функції “Пошук рішення” табличного процесора EXCEL На рис. 2.2 наведене діалогове вікно функції “Пошук рішення” табличного процесора EXCEL, де описані: - цільова клітка В15; - напрямок оптимізації - мінімізація; - діапазон змінюваних кліток - C10:F13; - обмеження задачі, які задані у вигляді однієї нерівності (C10:F1# >= 0) і двох рівностей (C7:F7 = C14:F14 і G3:G6 = G10:G13).
Рис. 2.2. Діалогове вікно функції “Пошук рішення” табличного процесора EXCEL ТРАНСПОРТНИХ ПЕРЕВЕЗЕНЬ ВАРІАНТИ ЗАВДАНЬ
Варіант завдання вибирається наступним чином: - відстані lij - по останній цифрі залікової книжки (табл. 3.1); - значення ai та bj - по передостанній цифрі залікової книжки (табл. 3.2). - для всіх варіантів прийняти m = 3; n = 5. Таблиця 3.1
Таблиця 3.2
ЛАБОРАТОРНОЇ РОБІТИ
Процес пошуку опорного та оптимального планів перевезень у транспортної (T) задачі розглянемо на конкретному прикладі. Відмітимо також, що всі без винятку спрощені методи розв’язання Т-задачі базуються на транспортній таблиці (див. табл. 3.3). В центрі кожної клітинки перехрестя Таблиця 3.3 Складання опорного плану перевезень ВАРІАНТИ ЗАВДАНЬ
Додати до транспортної мережі без обмежень на пропускні здатності (рис. 4.1) та транспортної мережі з обмеженнями на пропускні здатності замовлень (рис. 4.2)один пункт постачання з обсягом 5 одиниць вантажу, один пункт споживання з обсягом 5 одиниць вантажу та один проміжний транспортний пункт.
ЛАБОРАТОРНОЇ РОБОТИ На рис. 4.1 зображена мережа з 7 вершинами і 11 ланками. Поруч із відповідною вершиною у дужках числом зі знаком плюс показаний обсяг виробництва, а обсяг споживання, відповідно, числом зі знаком мінус. Вартість перевезення вантажу вписана в кожну дугу. Також на рис. 4.1 подані розподіли вантажопотоків і потенціалів.
Рис. 4.1. Приклад ТМ без Рис. 4.2. Приклад ТМ з обмежень на пропускні здатності обмеженнями на пропускні здатності Перший спосіб – Ордена А. показаний у табл. 4.1. Кожній вершині мережі виділяється рядок і стовпець. Таким чином у нашому випадку, таблиця складається із семи рядків і семи стовпців. Вона завжди повинна бути квадратною. У клітинках головної діагоналі таблиці 4.1, 2.2 і т. д. вартість перевезення дорівнює 0, тому що вихідних і одночасно вхідних дуг до тієї самої вершини бути не може. Для вершин, з'єднаних між собою ланкою, у клітинках таблиці на перетинанні відповідних рядків і стовпців проставлена вартість транспортування цією ланкою. Інші клітинки заблоковані більшими, порівняно з вартостями перевезень, числами (у табл. 4.1 це незаповнені клітинки). Для зручності розрахунку до значення обсягу виробництва (споживання) до кожної вершини додається яке-небудь позитивне число. У табл. 4.1 це число 9. Таким чином, обсяг виробництва у вершині 1 буде 7+9=16, у транзитній вершині 2 – 9, так само як і обсяг споживання і т. д. Потім ТЗ розв'язують будь-яким відомим методом. У табл. 4.1 показаний остаточний результат рішення задачі – значення оптимального плану перевезень вантажу виділені курсивом, а на рис. 4.3 – результат розв'язання за допомогою Excel-таблиці. Таблиця 4.1 Методом Ордена
Рис. 4.3. Розв'язання мережевої ТЗ без обмежень на пропускні здатності за допомогою Excel-таблиці Другий спосіб – спосіб Вагнера Ш.М. Він зручніший для мереж з обмеженнями пропускної здатності. Така мережа зображена на рис. 4.2, де представлений також і оптимальний план перевезень. У табл. 4.2 показано приведення цієї мережі до матричної форми. Таблиця 4.2 ВАРІАНТИ ЗАВДАНЬ
Додати до структури транспортної мережі (рис. 5.1) транспортний вузол з наведеної нижче карти. ЛАБОРАТОРНОЇ РОБОТИ Класичними задачами на графах є задачі про побудову найкоротших шляхів та їх сукупностей у вигляді відповідних дерев чи контурів. Однією з таких задач є пошук найкоротшого шляху між двома заданими вузлами: s (джерелом) і t (стоком). Розглянемо розв'язання цієї задачі на конкретному прикладі, який узятий з електронного атласу України:
Задана сітка у вигляді змішаного зваженого графа з 9 вузлами і 13 дугами, початкові дані мають наступний вигляд у Excel -таблиці(див. рис. 5.1). Треба визначити найкоротший шлях від вузла –джерела міста Київа до вузла-стоку міста Суми в следующей математической постановке: - знайти вектор Х = (х1, х2, … х13), де елемент хi = 1, якщо відповідна дуга належить найкоротшому шляху, і 0 у противному випадку; і – порядковий номер дуги (і = 1, 2,..., 13); - щоб загальна довжина шляху - за умови збереження балансу потоків для кожного j -го вузла (j = 1, 2,..., 9): Fвих (xi) - Fвх (xi) = 0, де Fвих (xi), Fвх (xi) – сума потоків на вході та виході кожного j -го вузла; для вузла-джерела Fвих (xi) - Fвх (xi) = 1; для вузла –стока Fвих (xi) - Fвх (xi) = -1; - при всіх xi ≥ 0.
Рис. 5.1. Топологія сітьової транспортної задачі Для цього в Excel -таблиці (далі просто таблиці) для всіх дуг визначити діапазон для невідомих Х (Дуга) і обчислити значення цільової функції за формулою = СУММПРОИЗВ(Дуга; Довжина), а для всіх вузлів обчислити суми вхідних (Вхід) і вихідних (Вихід) потоків, їх алгебраїчну суму (Вихід-Вхід), задати колонку правих частин обмежень (Обмеження). Для обчислення потоку у вузлах використовується функція обчислення суми величин, координати яких задовольняють визначеній умові (тобто, якщо певні величини належать відповідній множині). В Excel таку процедуру виконує функція СУММЕСЛИ(аргументи). Наприклад, сума вхідних потоків вузла визначається за формулою = СУММЕСЛИ(всі кінці дуг; вузол; потоки), тобто, підсумовуються потоки по тих дугах, кінці яких співпадають з поточним вузлом. За формулою = СУММЕСЛИ(всі початки дуг; вузол; потоки) підсумовуються вихідні потоки. На рис. 5.2 показане розв'язання поставленої задачи за допомогою команди Пошук рішення в середовищі Excel - програми, з котрого видно, що ветор Х = (0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1), а це, у свою чергу означає, що найкоротший шлях з міста Києва в місто Суми пройде послідовно через міста Березань, Пирятин і Гадач і складе 378 км.
Рис. 5.2. Розв'язання задачі про найкоротший шлях на мережі Задача про максимальний потік у мережі. Задача про максимальний потік на мережі – класична потокова задача, де параметром кожної дуги змішано-орієнтованої мережі є її максимальна пропускна здатність. Ця задача та її варіанти знаходять свое застосування при дослідженні потоків (величин і напрямків) транспортних мереж різного типу (шляхи, трубопроводи, канали зв’язку) для руху пасажирів, транспортних засобів, газу, інформації тощо. Результат рішения цієї задачі вказує величину максимального загального потоку, який може пропустити вся мережа, потоки та їх напрямки по окремих дугах. Розглянемо розв’язання задачі про максимальний потік у мережі на конкретному прикладі, який також узятий з електронного атласу України у вигляді зваженого графа з 6 вузлами і 11 дугами (топологія розглянутого графа збігається з топологією графа на рис. 5.1, де максимальний потік знаходився методом дерев), початкові дані мають наступний вигляд у Excel -таблиці (див. рис. 5.3).
Рис. 5.3. Розв'язання задачі про максимальний потік у сітці
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 217; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.147.190 (0.15 с.) |
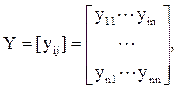
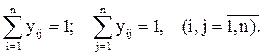
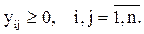
, залишаючись у теж час ненегативними. Тому величина 
Уточнена оцінка знизу довжин ГК
.
, то для групи оцінка знизу зросте на di,j, оскільки заздалегідь відомо, що ця дуга ввійде в усі ГК. Вона може ще зрости, якщо таблиця при викреслюванні i- ого рядка й j- ого стовпця буде допускати подальше приведення. У той же час при заміні елемента di,j на нескінченність МВ залишиться наведеної, тобто оцінка знизу для 
Значення цієї величини одержуємо шляхом додавання найменших чисел i-ого рядка й j-ого стовпця.
виходять рівними:
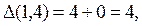
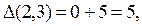
= 17.
і 
проставляються обсяги відповідних перевезень (
), у її верхньому правому куті – відповідні відстані від 
.
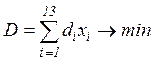, де di – довжина і -ої дуги;
