
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Составное (сложное) движение точкиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Составное движение точки - это такое движение, при котором точка одновременно участвует в двух или нескольких движениях. Рассмотрим тело А (рис. 28), которое свободно движется по отношению к неподвижной системе координат О1 x 1 y 1 z 1. Пусть точка М совершает движение по поверхности этого тела. Через произвольную точку О движущегося тела проведем неизменно связанные с этим телом оси x, y, z. Систему осей О xyz называют подвижной системой отсчета. Движение точки М по отношению к неподвижной системе отсчета называют абсолютным движением точки. Абсолютное движение точки характеризуется изменением радиуса-вектора Скорость и ускорение точки в абсолютном движении называют абсолютной скоростью и абсолютным ускорением точки и обозначают
Рис. 28
Движение точки М по отношению к подвижной системе отсчета называют относительным движением точки. Относительное движение характеризуется изменением только радиуса-вектора Скорость и ускорение точки в относительном движении называют относительной скоростью и относительным ускорением и обозначают Движение подвижной системы отсчета О xyz и неизменно связанного с ней тела А по отношению к неподвижной системе отсчета О1 x 1 y 1 z 1 является для точки М переносным движением. Переносное движение точки М характеризуется изменением радиусов-векторов Скорость и ускорение той точки тела А, с которой в данный момент совпадает точка М, называют переносной скоростью и переносным ускорением точки М и обозначают Желая изучить относительное движение точки, следует мысленно остановить переносное движение. Если необходимо изучить переносное движение точки, то надо мысленно остановить относительное движение и рассмотреть далее движение точки по формулам кинематики точки в абсолютном движении. Если точка М участвует в составном движении, то имеют место следующие теоремы: абсолютная скорость точки равна геометрической сумме переносной и относительной скоростей точки, т. е.
абсолютное ускорение точки равно геометрической сумме переносного, относительного и кориолисова (поворотного) ускорений этой точки, т. е.
или
Кориолисово ускорение
Следовательно, модуль этого ускорения
где a - угол между векторами Чтобы найти направление кориолисова ускорения
Рис. 29 Направление вектора Проведем через точку М плоскость П, перпендикулярную к вектору
Задача К3
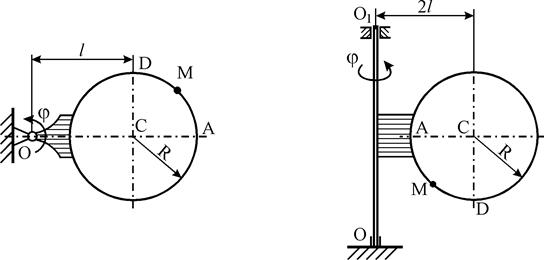
Прямоугольная пластина (рис. К3.0–К3.4) или круглая пластина радиуса R = 60 см (рис. К3.5–К3.9) вращается вокруг неподвижной оси по закону j = f1 (t), заданному в табл. К3. Положительное направление отсчета угла j показано на рисунках дуговой стрелкой. На рис. К3.0, К3.1, К3.2, К3.5, К3.6 ось вращения перпендикулярна плоскости пластины и проходит через точку О (пластина вращается в своей плоскости); на рис. К3.3, К3.4, К3.7, К3.8, К3.9 ось вращения О1О лежит в плоскости пластины (пластина вращается в пространстве). По пластине вдоль прямой ВD (рис. К3.0–К3.4) или по окружности радиуса R (рис. К3.5–К3.9) движется точка М; закон ее относительного движения, т. е. зависимость s = AM = f 2 (t) (s выражено в сантиметрах, t – в секундах), задан в табл. К3 отдельно для рис. К3.0–К3.4 и для рис. К3.5–К3.9; там же даны размеры b и l. На рисунках точка М показана в положении, при котором s = AM > 0 (при s < 0 точка М находится по другую сторону от точки А). Найти абсолютную скорость и абсолютное ускорение точки М в момент времени t1 = 1 с. Указания. Задача К3 – на сложное движение точки. Для ее решения воспользоваться теоремами о сложении скоростей и о сложении ускорений. Прежде чем производить все расчеты, следует по условиям задачи определить, где находится точка М на пластине в момент времени t1 = 1 с, и изобразить точку именно в этом положении (а не в произвольном, показанном на рисунках к задаче). В случаях, относящихся к рис. К3.5–К3.9, при решении задачи не подставлять числового значения R, пока не будут определены положение точки М в момент времени t1 = 1 с и угол между радиусами СМ и СA в этот момент.
Таблица К3
Рис. К3.0 Рис. К3.1 Рис. К3.2
Рис. К3.3 Рис. К3.4 Рис. К3.5
Рис. К3.6 Рис. К3.7
Рис. К3.8 Рис. К3.9
Рассмотрим два примера решения этой задачи. Пример К3а. Пластина OEAB1D (OE = OD, рис. К3а) вращается вокруг оси, проходящей через точку О перпендикулярно плоскости пластины, по закону j = f 1(t) (положительное направление отсчета угла j показано на рис. К3а дуговой стрелкой). По дуге окружности радиуса R движется точка В по закону s = Дано: R = 0,5 м, j = t2 - 0,5t3, s = p×R×cos(pt/3) (j - в радианах, s - в метрах, t - в секундах). Определить: Решение. Рассмотрим движение точки В как сложное, считая ее движение по дуге окружности относительным, а вращение пластины – переносным движением. Тогда абсолютная скорость
где, в свою очередь,
Рис. К3а
Определим все входящие в равенства (58) величины. 1. Относительное движение. Это движение происходит по закону
s =
Сначала установим, где будет находиться точка В на дуге окружности в момент времени t1. Полагая в уравнении (59) t1 = 2 с, получаем
s = p×R× cos(2p/3) = - 0,5pR.
Тогда
Знак минус свидетельствует о том, что точка В в момент t1 = 2 с находится справа от точки А. Изображаем ее на рис. К3а в этом положении (точка В1). Теперь находим числовые значения
где rотн – радиус кривизны относительной траектории, равный радиусу окружности R. Для момента t1 = 2 с, учитывая, что R = 0,5 м, получаем
Знаки показывают, что вектор 2. Переносное движение. Это движение (вращение) происходит по закону j = t2 – 0,5×t3. Найдем сначала угловую скорость w и угловое ускорение e переносного вращения:
и при t1 = 2 с w = – 2 c–1, e = – 4 с–2. (61)
Знаки указывают, что в момент t1 = 2 с направления w и e противоположны направлению положительного отсчета угла j; отметим это на рис. К3а. Для определения
Vпер = |w|×h1 = 2,82 м/с,
Изображаем на рис. К3а векторы 3. Кориолисово ускорение. Модуль кориолисова ускорения определяем по формуле а кор = 2× |Vотн| × |w| × sin a, где a – угол между вектором
а кор = 5,68 м/с2. (63) Направление Таким образом, значения всех входящих в правые части равенств (58) векторов найдены и для определения Vабс и а абс остается только сложить эти векторы. Произведем это сложение аналитически. 4. Определение Vабс. Проведем координатные оси В1ху(см. рис. К3 а) и спроектируем почленно обе части равенства
Vабс х = Vотн х + Vпер х = 0 - |Vпер| × сos 45° = - 1,99 м/с,
Vабс у = Vотн у + Vпер у = |Vотн| + |Vпер| × сos 45° = 3,41 м/с.
После этого находим
Учитывая, что в данном случае угол между
5. Определение а абс. По теореме о сложении ускорений
Для определения
а абс х =
а абс y =
Подставив сюда значения, которые все величины имеют в момент времени t1 = 2 с, найдем, что в этот момент
а абс х = 9,74 м/с2; а абс y = 7,15 м/с2.
Тогда
Ответ: Vабс = 3,95 м/с, а абс = 12,08 м/с2. Пример К3б. Треугольная пластина ADE вращается вокруг оси z по закону j = f 1(t) (положительное направление отсчета угла j показано на рис. К3б дуговой стрелкой). По гипотенузе AD движется точка Впо закону s = АВ = f 2(t); положительное направление отсчета s – от А к D. Дано: j = 0,1× t3–2,2× t, s = АВ = 2 + 15× t – 3×t2; (j – в радианах, s – в сантиметрах, t – в секундах). Определить: Vабс и а абс в момент времени t1 = 2 с. Решение. Рассмотрим движение точки В как сложное, считая ее движение по прямой AD относительным, а вращение пластины – переносным. Тогда абсолютная скорость
где, в свою очередь, Определим все входящие в равенство (65) величины. 1. Относительное движение - это движение прямолинейное и происходит по закону s = AB = 2 + 15t - 3t2, (66) Поэтому
В момент времени t1 = 2 с имеем
s1 = AB1 = 20 cм, Vотн = 3 см/с, а отн = - 6 см/с2. (67) Знаки показывают, что вектор
Рис. К3б 2. Переносное движение. Это движение (вращение) происходит по закону j = 0,1×t3 - 2,2t. Найдем угловую скорость w и угловое ускорение e переносного вращения: w =
w = - 1 c-1, e = 1,2 c-2. (68)
Знаки указывают, что в момент t1 = 2 с направление e совпадает с направлением положительного отсчета угла j, а направление w ему противоположно; отметим это на рис. К3б соответствующими дуговыми стрелками. Из рисунка находим расстояние h1 точки В1 от оси вращения z: h1 = AB1× sin 30° = 10 см. Тогда в момент t1 = 2 с, учитывая равенства (68), получаем: Vпер = |w|×h1 = 10 cм/с,
Изобразим на рис. К3б векторы 3. Кориолисово ускорение. Так как угол между вектором а кор = 2×|Vотн| × |w| × sin 30° = 3 см/с2. (70)
Направление 4. Определение Vабс. Так как 5. Определение а абс. По теореме о сложении ускорений
Для определения а абс проведем координатные оси В1хуz1 и вычислим проекции
а абс х = |
а абс у =
а абс z = | а отн|×cos 30 ° = 5,20 см/с2.
Отсюда находим значение а абс:
Ответ: Vабс = 10,44 см/с, а абс = 16,64 см/с2.
Вопросы для самоконтроля
1. Что понимается под составным (сложным) движением точки? 2. Что называется абсолютным, переносным и относительным движением точки? 3. Сформулируйте, что такое переносная скорость и переносное ускорение точки. 4. В чем заключается теорема об абсолютной скорости точки, совершающей составное движение. 5. Сформулируйте теорему об ускорениях точки в составном движении. 6. Как определить модуль и направление кориолисова ускорения точки? 7. В каких случаях ускорение Кориолиса равно нулю?
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1134; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.013 с.) |

 по модулю и направлению.
по модулю и направлению. и
и  .
.
 при неизменных радиусах-векторах
при неизменных радиусах-векторах 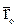 . В этом случае координаты х, у, z точки М в подвижной системе отсчета будут изменяться.
. В этом случае координаты х, у, z точки М в подвижной системе отсчета будут изменяться. и
и  .
. и
и  .
. =
= 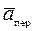 +
+ 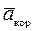 ,
, +
+ 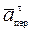 +
+  +
+ 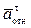 +
+ 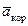 .
. равно удвоенному векторному произведению угловой скорости переносного вращения на относительную скорость точки, т. е.
равно удвоенному векторному произведению угловой скорости переносного вращения на относительную скорость точки, т. е. ´
´ 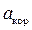 = 2 × wпер × Vотн × sin a,
= 2 × wпер × Vотн × sin a, и
и  точки М, достаточно в точке М построить векторы
точки М, достаточно в точке М построить векторы  и восстановить из этой точки перпендикуляр к плоскости, в которой лежат эти векторы
и восстановить из этой точки перпендикуляр к плоскости, в которой лежат эти векторы 
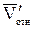 повернем в плоскости П на 90° вокруг точки М в направлении переносного вращения, то получим направление вектора
повернем в плоскости П на 90° вокруг точки М в направлении переносного вращения, то получим направление вектора 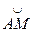 = f 2(t)
= f 2(t)



 = f 2(t) (положительное направление отсчета s – от A к B).
= f 2(t) (положительное направление отсчета s – от A к B). и
и 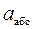 в момент времени t1 = 2 с.
в момент времени t1 = 2 с. и абсолютное ускорение
и абсолютное ускорение  +
+  +
+  +
+  ,
,  =
=  +
+  .
.
 = p×R× cos(pt/3). (59)
= p×R× cos(pt/3). (59)
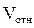 ,
, 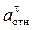 ,
,  :
: ,
, ,
, 
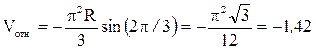 м/с,
м/с, м/с2,
м/с2,  м/с2. (60)
м/с2. (60) направлен в сторону положительного отсчета расстояния s, а вектор
направлен в сторону положительного отсчета расстояния s, а вектор  – в противоположную сторону; вектор
– в противоположную сторону; вектор  = 2×t – 1,5×t2,
= 2×t – 1,5×t2,  = 2 – 3×t;
= 2 – 3×t;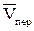 и
и  = 1,41 м. Тогда в момент времени t1 = 2 с, учитывая равенства (61), получим
= 1,41 м. Тогда в момент времени t1 = 2 с, учитывая равенства (61), получим = |e|×h1 = 5,64 м/с2,
= |e|×h1 = 5,64 м/с2,  = w2×h1 = 5,64 м/с2. (62)
= w2×h1 = 5,64 м/с2. (62)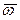 ). В нашем случае этот угол равен 90°, так как ось вращения перпендикулярна плоскости пластины, в которой расположен вектор
). В нашем случае этот угол равен 90°, так как ось вращения перпендикулярна плоскости пластины, в которой расположен вектор  найдем по правилу Н. Е. Жуковского: так как вектор
найдем по правилу Н. Е. Жуковского: так как вектор  на рис. К3а. (Иначе направление
на рис. К3а. (Иначе направление  ´
´  =
=  +
+  на эти оси. Получим для момента времени t 1 = 2 с:
на эти оси. Получим для момента времени t 1 = 2 с: м/с.
м/с.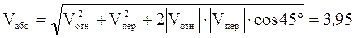 м/с.
м/с. =
=  +
+ 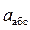 спроецируем обе части равенства (64) напроведенные оси В1ху. Получим:
спроецируем обе части равенства (64) напроведенные оси В1ху. Получим: + а кор +
+ а кор +  |.
|.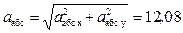 м/с2.
м/с2. найдутся по формулам:
найдутся по формулам: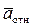 +
+ 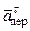 +
+  .
.

 – в противоположную сторону. Изображаем эти векторы на рис. К3б.
– в противоположную сторону. Изображаем эти векторы на рис. К3б.
 = 0,3t2 - 2,2; e =
= 0,3t2 - 2,2; e =  = 0,6t и при t1 = 2 с,
= 0,6t и при t1 = 2 с, = |e|×h1 = 12 см/с2,
= |e|×h1 = 12 см/с2, 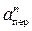 = w2×h1 = 10 см/с2. (69)
= w2×h1 = 10 см/с2. (69) (с учетом знаков w и e)и
(с учетом знаков w и e)и  ; направлены векторы
; направлены векторы  найдем по правилу Н. Е. Жуковского. Для этого вектор
найдем по правилу Н. Е. Жуковского. Для этого вектор  ; в момент времени t1 = 2 с Vабс = 10,44 см/с.
; в момент времени t1 = 2 с Vабс = 10,44 см/с. см/с2.
см/с2.


