
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вероятностные оценки погрешности результата измерения
Цель обработки результатов наблюдений – это установление действительного значения измеряемой величины, которое может быть принято вместо истинного значения измеряемой величины, и степени близости действительного значения к истинному. Действительное значение неизбежно содержит случайную погрешность. Для количественной оценки случайных погрешностей и установления границ случайной погрешности результата измерения могут использоваться: предельная погрешность, интервальная оценка, числовые характеристики закона распределения. Выбор конкретной оценки определяется необходимой полнотой сведений о погрешности, назначением измерений и характером использования их результатов. Комплексы оценок показателей точности установлены стандартами. Когда при проведении с одинаковой тщательностью и в одинаковых условиях повторных наблюдений одной и той же постоянной величины получаем результаты, отличающиеся друг от друга, это свидетельствует о наличии в них случайных погрешностей. Методы теории вероятностей и математической статистики позволяют установить вероятностные (статистические) закономерности появления случайных погрешностей и на основании этих закономерностей дать количественные оценки результата измерения и его случайной погрешности. Из теории вероятности известно, что оценкой математического ожидания является среднее арифметическое результатов отдельных наблюдений -
где
Оценка дисперсии ряда наблюдений
Среднее квадратическое отклонение ряда наблюдений
при n à Для расчета среднего квадратического отклонения результата измерения
Среднее квадратическое отклонение результата измерения Основными понятиями при статистических оценках являются понятия доверительного интервала и доверительной вероятности.
Доверительным интервалом называется интервал, в который с заданной доверительной вероятностью попадают значения случайной величины (погрешности). Доверительный интервал выражается в виде
где
Так для равномерного закона распределения Доверительные границы случайной погрешности Значение и знак случайной погрешности определить невозможно. Для учета случайной погрешности проводят многократные (статистические) измерения. Оценивая случайную погрешность, говорят об ожидаемой погрешности. Грубая погрешность – это случайная погрешность, существенно превышающая ожидаемую погрешность при данных условиях. Промах – погрешность, которая явно искажает результат измерения. За промах принимают случайную субъективную погрешность экспериментатора. Доверительному интервалу ±3
Задача №1 В результате проведенных измерений оказалось, что наиболее вероятное содержание кислорода в газовой смеси составляет Х =11,75%. Доверительный интервал погрешности измерения определялся для доверительной вероятности
Определить границы доверительного интервала при доверительной вероятности Варианты индивидуальных заданий приведены в Приложении В, таблица В1.
Пример решения задачи №1 При нормальном законе распределения погрешностей при доверительной вероятности 0,683 доверительные границы случайной погрешности определяют по таблице П1-4-1 [1]:
Ответ:
Задача №2 Определить границы доверительного интервала погрешности измерения температуры с вероятностью Р, если при большом числе измерений были получены среднее арифметическое результата наблюдений Варианты индивидуальных заданий приведены в Приложении В, таблица В2.
Задача № 3 В результате большого числа измерений термо-ЭДС был определен доверительный интервал Варианты индивидуальных заданий приведены в Приложении В, таблица В3.
Задание №2
|
||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 2518; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.130.218 (0.009 с.) |
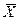
 , (3.1)
, (3.1) - i-й результат наблюдения;
- i-й результат наблюдения; - число результатов наблюдений.
- число результатов наблюдений. рассчитывается по формуле
рассчитывается по формуле .
. является основной характеристикой размера случайных погрешностей результатов наблюдений. Формула для расчета оценки среднего квадратического отклонения s
является основной характеристикой размера случайных погрешностей результатов наблюдений. Формула для расчета оценки среднего квадратического отклонения s = +
= +  , (3.2)
, (3.2) (практически при n > 30), S2 à D, S à s.
(практически при n > 30), S2 à D, S à s. используется формула
используется формула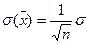 . (3.3)
. (3.3)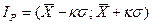 , (3.4)
, (3.4) - квантильный множитель, значение которого зависит от выбранного закона распределения случайной погрешности.
- квантильный множитель, значение которого зависит от выбранного закона распределения случайной погрешности.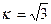 и не зависит от доверительной вероятности. Для нормального закона распределения
и не зависит от доверительной вероятности. Для нормального закона распределения  зависит от значения доверительной вероятности Р и количества выборочных значений n; значения
зависит от значения доверительной вероятности Р и количества выборочных значений n; значения  x, соответствующие доверительной вероятности Р, находят по формуле
x, соответствующие доверительной вероятности Р, находят по формуле  .
. = 0,683 и составил
= 0,683 и составил 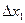 =
= 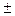 0,5%
0,5%  .
. = 0,95, если известно, что закон распределения погрешностей нормальный.
= 0,95, если известно, что закон распределения погрешностей нормальный. . При доверительной вероятности 0,95
. При доверительной вероятности 0,95  . Таким образом, числовое значение доверительного интервала для доверительной вероятности 0,95 составит
. Таким образом, числовое значение доверительного интервала для доверительной вероятности 0,95 составит  . Границы доверительного интервала по (3.4) будут равны
. Границы доверительного интервала по (3.4) будут равны .
. .
.
 . Предполагается нормальный закон распределения погрешности.
. Предполагается нормальный закон распределения погрешности. , мВ, с доверительной вероятностью Р. Определить среднюю квадратическую погрешность
, мВ, с доверительной вероятностью Р. Определить среднюю квадратическую погрешность 


