
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчетно-графическая работа № 2. Стандартная обработкаСтр 1 из 6Следующая ⇒
МЕТРОЛОГИЯ И ИЗМЕРЕНИЯ Методические указания к выполнению расчетно-графических работ (для студентов специальности 050702– Автоматизация и управление)
Алматы 2009
СОСТАВИТЕЛЬ: С.Г. Хан. Метрология и измерения. Методические указания к выполнению расчетно-графических работ (для студентов всех форм обучения специальности 050702 – Автоматизация и управление). – Алматы: АИЭС, 2009. – 48 с.
Методические указания содержат задания и рекомендации к выполнению трех расчетно-графических работ и предполагают самостоятельное изучение и решение задач по обработке результатов однократных прямых и косвенных измерений, многократных измерений, а также изучение и решение задач по оценке основных и дополнительных погрешностей средств измерений. Методические указания используются при выполнении расчетно-графических работ по дисциплине «Метрология и измерения». Библиогр.- 10 назв.
Рецензент: канд. техн. наук, доцент кафедры ИК АИЭС Л.К. Ибраева
Печатается по плану издания некоммерческого акционерного общества «Алматинский институт энергетики и связи» на 2009 г.
© НАО «Алматинский институт энергетики и связи», 2009 г. Содержание с. Введение…………………………………………………………………….4 1 Расчетно-графическая работа № 1. Способы числового выражения погрешностей средств измерений …………………...............5 1.1 Задание №1......................................................................................5 Расчетно-графическая работа № 2. Стандартная обработка результатов однократных прямых и косвенных измерений.....................10 2.1 Задание №1.....................................................................................10 2.1.1 Правила округления результата измерения ………………….12 2.2 Задание №2…….............................................................................14 Расчетно-графическая работа № 3. Стандартная обработка результатов многократных измерений…………………………................19 3.1 Задание №1………………………………………………………..19 3.2 Задание №2………………………………………………………..22 Приложение A.................................................................................................27 Приложение Б……………………………………………………………….31 Приложение В…………………………………………………………...…..35 Список литературы.........................................................................................47
Введение
Дисциплина «Метрология и измерения» изучается студентами специальности «Автоматизация и управление» на 2 курсе в пакете базовых дисциплин (обязательный компонент), объем 3 кредита Знания материала данной дисциплины для будущих специалистов (бакалавров, инженеров) технического профиля, связанных с разработкой или обслуживанием различного оборудования или средств измерительной техники, на наш взгляд является обязательными. Рабочая программа дисциплины «Метрология и измерения» включает большой объем теоретического и практического материала. Однако ограниченность аудиторных часов не позволяет в полной мере изложить необходимую информацию, поэтому большая часть материала изучается студентами в рамках самостоятельной работы, к которой относится выполнение расчетно-графических работ. Предлагаемые методические указания к выполнению расчетно-графических работ (РГР) составлены в соответствии с рабочей программой дисциплины и содержат три работы. Первая РГР «Способы числового выражения погрешностей средств измерений» посвящена изучению способов расчета абсолютных, относительных, приведенных основных и дополнительных погрешностей средств измерений и включает решение пяти задач. Вторая РГР «Стандартная обработка результатов однократных прямых и косвенных измерений» включает решение двух задач по обработке результатам прямых измерений и двух задач по обработке результатов косвенных измерений. Третья РГР «Стандартная обработка результатов многократных измерений» посвящена вероятностным методам оценки погрешностей многократных измерений и включает решение четырех задач. Методические указания содержат три приложения (А, Б, В), в которых содержатся индивидуальные задания по каждой из 13 задач и необходимый справочный материал для их решения. Список необходимой литературы приведен в конце методических указаний. Выбор индивидуального варианта контрольных работ для студентов заочной формы обучения определяется номером зачетной книжки. Вариант выбирается по двум последним цифрам номера зачетной книжки. Если число, задаваемое двумя последними цифрами, больше 25, то вариант выбирается по последней цифре номера зачетной книжки.
РГР должны быть выполнены и оформлены в соответствии с требованиями фирменного стандарта Алматинского института энергетики и связи ФС РК 10352-1910-У-е-001-2002 «Работа учебные. Общие требования к построению, изложению, оформлению и содержанию».
Расчетно-графическая работа №1. Способы числового выражения погрешностей средств измерений
Цель работы: изучение способов расчета абсолютных, относитель-ных, приведенных основных и дополнительных погрешностей средств измерений.
Задание №1 Учет всех нормируемых метрологических характеристик средства измерений (СИ) при оценивании погрешности результата измерений, как видно, сложная и трудоемкая процедура, оправданная при измерениях повышенной точности. При измерениях на производстве, в обиходе такая точность не всегда нужна. В то же время, определенная информация о возможной инструментальной составляющей погрешности измерения необходима. Такая информация дается указанием класса точности средства измерений. Класс точности – обобщенная метрологическая характеристика (МХ), определяемая пределами основной и дополнительных допускаемых погрешностей, а также другими свойствами средств измерений, влияющими на точность. Класс точности - величина безразмерная. Классы точности присваивают средствам измерений при их разработке на основании исследований и испытаний представительной партии средств измерения данного типа. При этом пределы допускаемых погрешностей нормируют и выражают в форме абсолютных, приведенных или относительных погрешностей, в зависимости от характера изменения погрешностей в пределах диапазона измерений. От условий применения СИ различают следующие погрешности: 1) основная погрешность СИ- погрешность СИ, используемого в нормальных условиях (Н.У.). Под Н.У. применения СИ понимаются условия, при которых влияющие величины (температура окружающего воздуха, барометрическое давление, влажность, напряжение питания, частота тока и т.д.) имеют нормальные значения или находятся в пределах нормальной области значений, а также определенное пространственное их положение, отсутствие вибрации, внешнего электромагнитного поля, кроме земного магнитного поля. Н.У. обычно не являются рабочими условиями применения СИ; 2) под пределом допускаемой дополнительной погрешности понимается наибольшая дополнительная погрешность, вызываемая изменением влияющей величины в пределах расширенной области значений (РОЗ), при которой средство измерений может быть признано годным и допущено к применению. В стандартах или технических условиях для каждого вида СИ устанавливают расширенную область значений влияющих величин, в пределах которой значение дополнительной погрешности не должно превышать установленных пределов. Терминам основная и дополнительная погрешности соответствуют фактические погрешности СИ, имеющие место при данных условиях. От формы представления погрешности различают абсолютную, относительную и приведенную погрешности СИ. Абсолютная погрешность измерительного прибора – разность между показаниями прибора и действительным значением измеряемой величиной
Относительная погрешность измерительного прибора – отношение абсолютной погрешности измерительного прибора к действительному значению измеряемой величины
Приведенная погрешность измерительного прибора - отношение абсолютной погрешности измерительного прибора к нормирующему значению измеряемой величины
В качестве нормирующего значения Для рассматриваемого способа нормирования погрешностей средств измерений предел допускаемой основной погрешности показаний
Дополнительные погрешности средств измерений или изменение показаний измерительных приборов, вызываемые изменением i –ой влияющей величины на нормированное отклонение (или в пределах расширенной области), выражаются в виде приведенной погрешности в процентах нормирующего значения
где
Если в стандарте или монтажно-эксплуатационной инструкции указывается, что измерительный прибор предназначен для применения в рабочих условиях в расширенной области значений влияющей величины (РОЗ), это означает, что предел допускаемой дополнительной погрешности в пределах этой области нормирован.
Задача №1 Класс точности измерительного прибора равен Варианты индивидуальных заданий приведены в Приложении А, таблица А1.
Пример решения задачи №1 Согласно условия задачи, известны диапазон измерения прибора, его класс точности. Исходя из того, что класс точности численно равен приведенной погрешности, выраженной в процентах, то приведенная погрешность
Относительная погрешность определяется по формуле (1.2)
Ответ:
Задача №2 Измерительный прибор с диапазоном измерений 25 – 50 мВ класса точности Варианты индивидуальных заданий приведены в Приложении А, таблица А2.
Задача №3 При поверке термопары ТХА были получены следующие данные. Термо-ЭДС поверяемой термопары равно Температура комнаты равна Варианты индивидуальных заданий приведены в Приложении А, таблица А3.
Пример решения задачи №3 Заключение о поверке: годна или нет поверяемая термопара к применению, дается на основании сравнения расчетной абсолютной погрешности поверяемой термопары с ее пределом допускаемой основной абсолютной погрешности, заданной в основных технических характеристиках (см. таблица 4-7-3 [1]). Согласно таблице 4-7-3 предел допускаемой основной абсолютной погрешности термоэлектрического термометра (термопары) ТХА Расчет абсолютной погрешности поверяемой погрешности
где
Для получения результатов измерений температуры поверяемой и образцовой термопарами проведем следующие расчеты [10].
где Поскольку измерения проводятся при температуре комнаты По формуле (1.5) рассчитываются значения термо-ЭДС для поверяемой и образцовой термопар Термо-ЭДС поверяемой термопары
Термо-ЭДС образцовой термопары
Определим по полученным значениям термо-ЭДС и по соответствующим градуировочным таблицам значения измеряемой температуры, полученные поверяемой и образцовой термопарами: Определим абсолютную погрешность поверяемой термопары в
Определим абсолютную погрешность поверяемой термопары в Заключение о поверке:
Задача №4 Определить дополнительную абсолютную погрешность измерения температуры медным термометром сопротивления градуировки 50М, включенным по двухпроводной схеме, если значение сопротивления соединительных проводов равно Варианты индивидуальных заданий приведены в Приложении А, таблица А4.
Пример решения задачи №4 Коэффициент преобразования медного термометра сопротивления градуировки 50М (
Дополнительная абсолютная погрешность измерения температуры при отклонении сопротивления соединительных проводов от градуировочного равна
Ответ:
Задача №5 Расширенная область значений влияющих величин (РОЗ): от 0 Варианты индивидуальных заданий приведены в Приложении А, таблица А5.
Пример решения задачи №5 Погрешность показаний прибора равна
где
Основная погрешность измерительного прибора Для определения дополнительной погрешности найдем отклонение температуры окружающей среды от нормальной области значений Дополнительная погрешность измерительного прибора
Погрешность показаний прибора
Ответ:
Задание №1
Задача №1 Определить результат однократных измерений, если измерение проводилось в нормальных условиях и методическая погрешность была пренебрежительно мала. Результат измерения записать в соответствии с правилами округления (п.2.1.1.1). Варианты индивидуальных заданий приведены в Приложении Б, таблица Б1.
Пример решения задачи №1 Указатель отсчетного устройства вольтметра, имеющего верхний предел измерения 60 мВ, показывает 30 мВ, класс точности прибора 0,02/0,01. Определить результат однократных измерений вольтметра, если измерение проводилось в нормальных условиях и методическая погрешность была пренебрежительно мала. Решение. Поскольку класс точности задан в виде
С другой стороны, Ответ: Результат однократных измерений можно записать в виде
Задача №2 Выбрать класс точности и диапазон измерения для заданного средства измерения. Определить результат измерения, если измерение проводилось в нормальных условиях и методическая погрешность была пренебрежительно мала. Результат измерения записать в соответствии с правилами округления (п.2.1.1.1). Варианты индивидуальных заданий приведены в Приложении Б, таблица Б2.
Пример решения задачи №2 Выбрать класс точности и диапазон измерения вольтметра для измерения номинального напряжения 220 В с относительной погрешностью, не превышающей 1%. Записать результат измерения, если вольтметр показал 230 В, измерение проводилось в нормальных условиях и методическая погрешность была пренебрежительно мала. Решение. Поскольку номинальное значение параметра должно попадать во вторую половину диапазона измерений вольтметра, выбираем вольтметр с диапазоном измерения от 0 В до 300 В. Исходя из приведенного условия, для того чтобы относительная погрешность измерения не превысила 1% необходимо, чтобы модуль абсолютной погрешности измерений не превысил
Модуль приведенной погрешности вольтметра не может превысить
что соответствует классу точности 0,7. Приборы такого класса точности не выпускаются. Величины класса точности представляют собой числа, выбираемые из ряда (1; 1,5; 2; 2,5; 3; 4; 5; 6) 10
Ответ: Результат измерений записывается в виде
Задание №2 Задача №3 При измерении расхода калориметрическим расходомером измерение мощности нагревателя производится по показаниям амперметра и вольтметра. Оба эти прибора имеют класс точности Кл =0,5, работают в нормальных условиях и имеют соответственно шкалы 0-5 А и 0-30 В. Номинальные значения силы тока 3.5 А и напряжения 24 В. Оценить погрешность, с которой производится измерение мощности. Представить результат измерения мощности нагревателя в соответствии с правилами округления (п.2.1.1.1). Варианты индивидуальных заданий приведены в Приложении Б, таблица Б3.
Пример решения задачи №3 Погрешность измерения мощности нагревателя W оценивается как погрешность косвенного измерения по формуле
В связи с отсутствием каких-либо других метрологических характеристик средств измерений, кроме класса точности, можно определить только пределы допускаемых значений погрешности в соответствии с классом точности (Кл) и шкалой прибора (U
Известно, что мощность равна тогда Предел допускаемой абсолютной погрешности измерения мощности
Предел допускаемой относительной погрешности измерения мощности
Ответ: Результат измерения
Задача №4 При исследовании теплоотдачи от трубы к воздуху коэффициент теплоотдачи подсчитывается из выражения
Количество теплоты Q, передаваемой трубкой путем конвекции, определяется по мощности, потребляемой электронагревателем, как произведение сопротивления трубки R на квадрат силы тока I Сила тока измеряется амперметром со шкалой 0-50 А класса 0,1, номинальное значение тока 42 А. Основная погрешность измерения силы тока не должна превышать Зависимость сопротивления трубки от температуры была найдена в специальных опытах и описывается выражением
При t=0 значение сопротивления R Поверхность трубки F определяется по длине l и его диаметру d
Значение длины l = 100 Температура стенки трубки
где U – показания потенциометра, мВ; U U Температура воздуха Оценить погрешность измерения коэффициента теплоотдачи на лабораторной установке. Погрешностями, связанными с методами измерения, пренебречь. Результат измерения записать в соответствии с правилами округления (п.2.1.1.1). Варианты индивидуальных заданий приведены в Приложении Б, таблицы Б4, Б5 и Б6.
Пример решения задачи №4 Коэффициент теплоотдачи определяется как результат косвенных измерений параметров Q, F,
В связи с тем, что все измеряемые параметры определяются с допускаемыми отклонениями, которые можно считать предельными значениями погрешности, сам коэффициент теплоотдачи может быть оценен с каким-то пределом допускаемой погрешности. Количество теплоты Q определяется по мощности электронагревателя. Таким образом, Q в свою очередь является результатом косвенных измерений I и R. Температура трубки измерялась стандартным термоэлектрическим термометром градуировки ХК в комплекте с потенциометром ПП-63. Допускаемое отклонение термо-ЭДС термоэлектрического термометра ТХК от градуировочных значений при
Оценим предел суммарной погрешности
что соответствует Сопротивление трубки R определялось по измеренной температуре в соответствии с выражением (2.1)
Погрешность определения значения R обусловлена погрешностью прибора, измеряющего сопротивление, и погрешностью измерения температуры. Составляющая погрешности, обусловленная погрешностью прибора, не превышает
Составляющая погрешности, обусловленная погрешностью измерения температуры, не превышает
Оценим предел суммарной погрешности определения сопротивления нагреваемой трубки по ее температуре, полагая, что погрешность градуировки трубки и погрешность измерения температуры – независимые величины
или в относительных величинах Теперь можно оценить погрешность определения количества теплоты, передаваемой от трубки к воздуху
откуда
Оценим предел погрешности определения поверхности теплообменника F
Оценим погрешность измерения воздуха по характеристикам стеклянного термометра. Термометр с ценой деления 0,2 Для оценки предела погрешности определения коэффициента теплоотдачи воспользуемся формулой для определения абсолютной погрешности. Вначале определим производные
Расчетный коэффициент теплоотдачи
Предел допускаемой относительной погрешности
Ответ:
Задание №1 Задача №1 В результате проведенных измерений оказалось, что наиболее вероятное содержание кислорода в газовой смеси составляет Х =11,75%. Доверительный интервал погрешности измерения определялся для доверительной вероятности Определить границы доверительного интервала при доверительной вероятности Варианты индивидуальных заданий приведены в Приложении В, таблица В1.
Пример решения задачи №1 При нормальном законе распределения погрешностей при доверительной вероятности 0,683 доверительные границы случайной погрешности определяют по таблице П1-4-1 [1]:
Ответ:
Задача №2 Определить границы доверительного интервала погрешности измерения температуры с вероятностью Р, если при большом числе измерений были получены среднее арифметическое результата наблюдений Варианты индивидуальных заданий приведены в Приложении В, таблица В2.
Задача № 3 В результате большого числа измерений термо-ЭДС был определен доверительный интервал Варианты индивидуальных заданий приведены в Приложении В, таблица В3.
Задание №2 Варианты заданий В соответствии с приведенной выше методикой (п.3.2.1) провести обработку ряда наблюдений. Варианты индивидуальных заданий приведены в Приложении В, таблица В7.
Приложение А
Таблица А1- РГР №1, варианты задания №1, задача 1
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1219; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.87.156 (0.19 с.) |
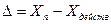 , (1.1)
, (1.1) определяется с помощью образцового прибора или воспроизводится мерой.
определяется с помощью образцового прибора или воспроизводится мерой. (1.2)
(1.2) . (1.3)
. (1.3) используется верхний предел измерения или диапазон измерений измерительного прибора.
используется верхний предел измерения или диапазон измерений измерительного прибора. , выраженный в процентах нормирующего значения
, выраженный в процентах нормирующего значения 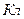 , принимаемым для обозначения класса точности средств измерений. Таким образом, исходя из того, что класс точности численно равен приведенной погрешности, выраженной в процентах, то предел допускаемой основной абсолютной погрешности показаний определяют по формуле
, принимаемым для обозначения класса точности средств измерений. Таким образом, исходя из того, что класс точности численно равен приведенной погрешности, выраженной в процентах, то предел допускаемой основной абсолютной погрешности показаний определяют по формуле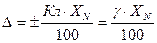 . (1.4)
. (1.4) , (1.5)
, (1.5) предел допускаемой дополнительной погрешности, %;
предел допускаемой дополнительной погрешности, %; - показание прибора или значение выходного сигнала преобразователя в данной точке шкалы (диапазона преобразования);
- показание прибора или значение выходного сигнала преобразователя в данной точке шкалы (диапазона преобразования); - показание прибора или значение выходного сигнала преобразователя в данной точке шкалы (диапазона преобразования) при нормальном значении или нормальной области значений влияющей величины (принимается за действительное значение).
- показание прибора или значение выходного сигнала преобразователя в данной точке шкалы (диапазона преобразования) при нормальном значении или нормальной области значений влияющей величины (принимается за действительное значение). 1,5. Диапазон измерения от
1,5. Диапазон измерения от  =–50
=–50 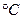 до
до  =+150
=+150 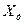 =70
=70  . Абсолютная погрешность определяется по формуле (1.4)
. Абсолютная погрешность определяется по формуле (1.4) .
. .
.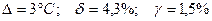 .
.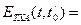 3,3 мВ. Термо-ЭДС образцовой термопары ТПП равно
3,3 мВ. Термо-ЭДС образцовой термопары ТПП равно  0,46 мВ.
0,46 мВ. 20 С. Дать заключение о поверке.
20 С. Дать заключение о поверке. .
. - результат измерения температуры поверяемой термопарой;
- результат измерения температуры поверяемой термопарой; , (1.5)
, (1.5) - поправка на температуру свободных концов термопары АВ, отличную от градуировочной температуры, равной
- поправка на температуру свободных концов термопары АВ, отличную от градуировочной температуры, равной  .
.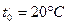 , т.е. свободные концы термопары находятся в комнате и их температура не равна
, т.е. свободные концы термопары находятся в комнате и их температура не равна  мВ и для термоэлектрического термометра ТПП (таблица П4-7-1, [1]):
мВ и для термоэлектрического термометра ТПП (таблица П4-7-1, [1]):  мВ.
мВ. , по которым определяется значение измеряемой температуры.
, по которым определяется значение измеряемой температуры. .
. .
.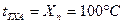 ,
,  .
. .
. . Для этого воспользуемся опять градуировочной таблицей термоэлектрического термометра ТХА:
. Для этого воспользуемся опять градуировочной таблицей термоэлектрического термометра ТХА:  .
.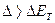 (
( ), поэтому поверяемая термопара ТХА не годна к применению для измерений температуры.
), поэтому поверяемая термопара ТХА не годна к применению для измерений температуры. =4,5 Ом вместо значения
=4,5 Ом вместо значения  =5 Ом. Температурный коэффициент электрического сопротивления меди
=5 Ом. Температурный коэффициент электрического сопротивления меди 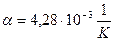 .
. Ом по градуировочной таблице для медного термосопротивления) равен
Ом по градуировочной таблице для медного термосопротивления) равен .
. .
. .
.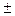 5
5 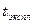 =40
=40  =
=  =10
=10  ,
, - пределы допускаемой основной погрешности измерительного прибора при его эксплуатации в нормальной области значений влияющих величин;
- пределы допускаемой основной погрешности измерительного прибора при его эксплуатации в нормальной области значений влияющих величин; :
:  .
. .
.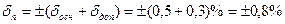 .
.
 .
.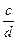 = 0,02/0,01, следовательно, для данного прибора предел основной погрешности, согласно таблице 1, вычисляется по формуле основной относительной погрешности
= 0,02/0,01, следовательно, для данного прибора предел основной погрешности, согласно таблице 1, вычисляется по формуле основной относительной погрешности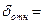
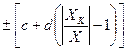 =
= 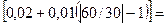
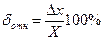 = 0,03%, отсюда предел основной абсолютной погрешности вольтметра не превышает
= 0,03%, отсюда предел основной абсолютной погрешности вольтметра не превышает 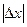
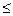 0,0003*30 мВ = 0,09мВ.
0,0003*30 мВ = 0,09мВ.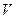 = (30,00
= (30,00  =
= 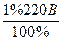 =2.2 В.
=2.2 В.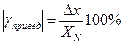 =2,2 В/300 В * 100% = 0,7%,
=2,2 В/300 В * 100% = 0,7%,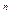 , где n=1; 0; -1; -2 и т.д. Поэтому выбираем вольтметр класса точности 0,6. Тогда модуль абсолютной погрешности измерений не превысит
, где n=1; 0; -1; -2 и т.д. Поэтому выбираем вольтметр класса точности 0,6. Тогда модуль абсолютной погрешности измерений не превысит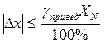 =
= 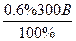 =1,8 В.
=1,8 В. .
. - U
- U  )
)

 ,
,



 .
.
 .
. А.
А. (2.1)
(2.1) =0,5 Ом,
=0,5 Ом,  . Погрешность измерения сопротивления не превышает
. Погрешность измерения сопротивления не превышает  .
. .
. измеряется стандартным термоэлектрическим термометром градуировки ХК. Термометр через сосуд свободных концов подсоединяется к лабораторному потенциометру ПП-63 класса 0,05. Номинальное значение температуры стенки 200
измеряется стандартным термоэлектрическим термометром градуировки ХК. Термометр через сосуд свободных концов подсоединяется к лабораторному потенциометру ПП-63 класса 0,05. Номинальное значение температуры стенки 200 
 - цена деления шкалы, мВ.
- цена деления шкалы, мВ. измеряется вдали от трубки ртутным термометром повышенной точности со шкалой 100 – 150
измеряется вдали от трубки ртутным термометром повышенной точности со шкалой 100 – 150  .
. составляет
составляет  мВ (см. табл.4-7-3 [1]). Предел допускаемой погрешности потенциометра ПП-63
мВ (см. табл.4-7-3 [1]). Предел допускаемой погрешности потенциометра ПП-63 мВ;
мВ;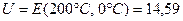 мВ.
мВ. измерения температуры в предположении, что погрешности термометра и потенциометра являются независимыми величинами. Тогда
измерения температуры в предположении, что погрешности термометра и потенциометра являются независимыми величинами. Тогда мВ,
мВ, или
или  .
. Ом.
Ом.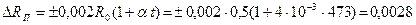 Ом.
Ом. Ом.
Ом. Ом
Ом .
. Вт,
Вт, Вт.
Вт. м
м  ;
;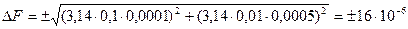 м
м  . Таким образом
. Таким образом  =
=  .
. ;
;
 ;
; ;
; .
. .
. .
. ,
, 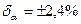 .
. = 0,683 и составил
= 0,683 и составил 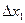 =
=  .
. = 0,95, если известно, что закон распределения погрешностей нормальный.
= 0,95, если известно, что закон распределения погрешностей нормальный. . При доверительной вероятности 0,95
. При доверительной вероятности 0,95  . Таким образом, числовое значение доверительного интервала для доверительной вероятности 0,95 составит
. Таким образом, числовое значение доверительного интервала для доверительной вероятности 0,95 составит  . Границы доверительного интервала по (3.4) будут равны
. Границы доверительного интервала по (3.4) будут равны .
. .
.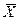 и дисперсия
и дисперсия  . Предполагается нормальный закон распределения погрешности.
. Предполагается нормальный закон распределения погрешности. , мВ, с доверительной вероятностью Р. Определить среднюю квадратическую погрешность
, мВ, с доверительной вероятностью Р. Определить среднюю квадратическую погрешность  измерения термо-ЭДС в предположении нормального закона распределения погрешности.
измерения термо-ЭДС в предположении нормального закона распределения погрешности.


