
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Арифметические и логические основыСтр 1 из 17Следующая ⇒
АРИФМЕТИЧЕСКИЕ И ЛОГИЧЕСКИЕ ОСНОВЫ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
УЧЕБНОЕ ПОСОБИЕ по курсу «Арифметические и логические основы вычислительной техники» для студентов специальности Т100300 ”Вычислительные машины, системы и сети”
Минск 2004
УДК 681.322 (075.8) ББК 32.97 я 73 Л 86
Рецензент: заведующий кафедрой математики и информатики ЕГУ, кандидат технических наук В.И. Романов
Луцик Ю.А.
УДК 681.322 (075.8) ББК 32.97 я 73
© Луцик Ю.А., Лукьянова И.В., 2004 ISBN 985-444-595-Х © БГУИР, 2004 Введение Основная цель настоящего учебного пособия - помочь студенту, приступившему к изучению арифметики вычислительных машин, приобрести теоретические знания и практические навыки выполнения основных арифметических операций. Правильное понимание алгоритмов рассматриваемых операций подкрепляется знанием структурных и логических схем, реализующих эти алгоритмы и представляющих собой некоторые операционные устройства. В пособии уделяется внимание рассмотрению этих схемных решений. Достаточно подробно рассмотрен аппарат, основанный на правилах и законах булевой алгебры, ориентированный на упрощение (минимизацию) проектируемых логических схем. Кроме того, в пособии приводятся сведения об основных формах хранения и преобразования числовой информации, способах ее кодирования. Достаточное внимание уделено методам контроля правильности функционирования цифрового автомата, возможным ошибкам, возникающим при его работе, и способам их устранения.
Рассматриваемый в пособии теоретический материал сопровождается достаточным количеством примеров, что упрощает и делает более понятным излагаемый материал. В заключение следует отметить, что в течение ряда лет литература, освещающая арифметику вычислительных машин, не выпускалась. В пособии сделана попытка устранить этот информационный пробел. Материал пособия базируется на работах [1-5].
Арифметические основы вычислительной техники Системы счисления В ЭВМ информация всегда представляется в виде чисел, записанных в той или иной системе счисления. Выбор системы счисления - один из важнейших вопросов. От правильности его решения зависят такие характеристики ЭВМ, как скорость вычислений, сложность алгоритмов реализации арифметических операций и др. Система счисления - совокупность цифр, приемов и правил для записи чисел цифровыми знаками. Любая система счисления должна обеспечивать: § возможность представления любого числа в рассматриваемом диапазоне величин; § единственность этого представления; § простоту оперирования числами. Различают два типа систем счисления - непозиционные и позиционные. Непозиционная система счисления - система, для которой значение символа не зависит от его положения в числе. Примером может служить система счисления с одной цифрой 1. Для записи любого числа в ней необходимо написать количество единиц, равное числу. Другой пример - это римская система счисления. Позиционной системой счисления называется система записи любых по величине чисел, в которой значение цифры зависит от ее положения в числе, т.е. веса. Число цифр в позиционной системе счисления ограниченно. Основание (базис) r позиционной системы счисления - максимальное количество различных знаков или символов, используемых для изображения числа в данной системе счисления. Таким образом, основание может быть любым числом, кроме 1 и бесконечности. Любое число в системе счисления с основанием r может быть записано в общем виде:
A=an·rn+ an-1·rn-1+...+a1·r1+a0·r0+ a-1·r--1+...+a-rn-1·r-(rn-1)+a-rn·r-rn, (1) или
где любая разрядная цифра aiÎ{0,…,r-1}, a ri - вес соответствующего разряда. Запись числа в форме (1) назовем записью числа в развернутой форме. Свернутой формой записи чисел называется запись чисел в виде A=a1a2 … ak. Для любой системы счисления основание представляется как 1 (один) и 0 (ноль). Например: 9 1 F 7 + 1 + 1 + 1 + 1 1010 102 1016 108 Вес разряда pi числа выражается соотношением pi = ri /r0 = ri, где i - номер разряда при отсчете справа налево. Если в i-м разряде накопилось значение единиц, равное или большее r, то должна происходить передача единицы в старший i+1 разряд. При сложении такая передача информации называется переносом. При вычитании передача из i+1 разряда в i-й – заем. Длина числа – количество позиций (разрядов) в записи числа. В технической реализации под длиной числа понимается длина разрядной сетки. Диапазон представления чисел в заданной системе счисления – интервал числовой оси, заключенный между максимальным и минимальным числами, представленными при заданной длине разрядной сетки. В вычислительной технике для представления данных и выполнения арифметических операций над ними удобно использовать двоичную, восьмеричную и шестнадцатеричную системы счисления. Ниже коротко остановимся на них.
Двоичная система счисления Для записи числа в двоичной системе счисления используются две цифры: 0 и 1. Основание системы записывается как 10(2) (210=1·21+0·20). Используя данную систему, любое число можно выразить последовательностью высоких и низких потенциалов или группой запоминающих элементов, способных запоминать одно из двух (0,1) значений. Арифметические операции в двоичной системе счисления выполняются по тем же правилам, что и в десятичной системе счисления.
Рассмотрим несколько примеров, демонстрирующих выполнение арифметических операций:

Перевод целых чисел Метод подбора степеней основания. В соответствии с (2) целые числа в системах счисления с основаниями r1 и r2 могут быть представлены: n k A r1 = i=0 j=0 В общем случае перевод числа из системы счисления с основанием r1 в систему счисления с основанием r2 можно представить как задачу определения коэффициентов bi нового ряда, изображающего число в системе счисления с основанием r2. Основная трудность в выборе максимальной степени основания r2, которая еще содержится в числе Ar1. Все действия должны выполняться по правилам r1-арифметики (то есть исходной системы счисления). После нахождения максимальной степени и соответствующего ей коэффициента необходимо найти коэффициенты для всех остальных (младших) степеней. Пример: A10=37, A2=? 37=1·25 + 0 ·24 + 0 ·23 + 1·22 + 0 ·21 + 1·20=100101. Нечетным двоичным числом 100101 является число, содержащее единицу в младшем разряде. Метод деления на основание системы счисления. На основании (1) число Ar1 в системе счисления с основанием r2 запишется в виде Ar2 = an· r2n + an-1 ·r2n-1 +... + a1· r21 + a0·r0. Переписав это выражение по схеме Горнера, получим:
Ar2 = (...(an r2 + an-1) r2 +... + a1) r2 + a0. Разделив правую часть на r2, получим первый остаток a0 и целую часть (...(an r2 + an-1) r2 +... + a1). Разделив целую часть на r2, получим остаток a1 и новую целую часть. Выполнив деление n+1 раз, получим последнее целое частное an < r2, являющееся старшей цифрой числа. Пример: А10 = 37, A2 =?, А5=?
Перевод правильных дробей Метод подбора величин, обратных степеням основания A10 =0,716 А2 =0,1011...
Количество разрядов после запятой зависит от точности, с которой требуется представить число. Метод умножения на основание r2 новой системы счисления. Из выражения (1) дробное число Ar1 в системе счисления с основанием r2 запишется в виде Ar2 = a-1 r2-1 +... + a-n r2-n. Переписав это выражение по схеме Горнера, получим: Ar2 = r2-1 (a-1 + r2-1 (a-2 +... + a-n r2-1)...). Умножив правую часть на r2, получим новую неправильную дробь, целая часть которой есть a-1 (старшая цифра числа Ar2). Продолжим процесс умножения дробной части на r2 n-1 раз, получим цифры a-2, a-3,... числа Ar2. Процесс умножения может быть прекращен, если во всех разрядах после очередного умножения получены нули либо достигнута требуемая точность. Пример: A10=0,673, A2=?, A16=?
Для перевода неправильных дробей отдельно выделяется целая и дробная части числа и с использованием соответствующих методов выполняется их перевод. Результаты записываются в виде новой неправильной дроби.
Кодирование чисел Кодирование знака числа. Кодирование чисел позволяет заменить операцию арифметического вычитания операцией алгебраического сложения с помощью двоичного сумматора. Для кодирования знака числа используется специальный двоичный разряд, называемый знаковым. При этом знак плюс кодируется двоичной цифрой 0, а минус – цифрой 1 (для системы счисления с основанием r – цифрой r-1). Для машинного представления отрицательных чисел используют три основных вида кодов: прямой, обратный и дополнительный. Общая схема кода числа: код знака. код числа. Прямой код числа. При этом способе кодирования чисел кодируется только знак числа, а значащая часть остается без изменения.
Пример: A=+0,1101 A= - 0,1101 [A]пр=0,1101 [A]пр=1,1101
Пример: A = + 1101 A = - 1101 [A]пр=0.1101 [A]пр=1.1101 Диапазон изменения машинных изображений для прямого кода лежит в пределах: -(1-2-n) Недостатком прямого кода является сложность выполнения операции сложения чисел с разными знаками. Для арифметических операций над числами в прямом коде используется сумматор прямого кода. В этом сумматоре отсутствует цепь поразрядного переноса между старшим значащим и знаковым разрядами, то есть на этом сумматоре невозможно выполнение операции алгебраического сложения.
Дополнительный код числа. Число А' называется дополнением к числу А, если выполняется соотношение: А + А¢ = rn для целых чисел или А + А'=r0 для дробных чисел, где n – количество цифр в записи числа A. Пример: A10 =378 n=3 A10' =103 – А10=1000 - 378=622 621 - все разряды дополняются до младшей цифры системы счисления
n=4 А2 =1011, Замена операции вычитания операцией сложения. В ЭВМ достаточно сложно выполнить операцию вычитания (А-В). Для этого требуется: 1) сравнить числа и выявить наибольшее из них по абсолютной величине; 2) наибольшее число разместить на входах вычитающего устройства; 3) выполнить операцию вычитания; 4) присвоить значению разности знак наибольшего по абсолютной величи- не числа. Для сложения чисел в дополнительных кодах требуется сумматор и неважно, какие слагаемые подаются на его входы А или В. Пусть необходимо сложить А = 487 А = 487 В = -348 В = 652 А-В = 139 А-В = 1 139 А + (103 – В) = А-В+103 (103 игнорируется). А = 348 А = 348 В = -487 В = 513 А-В = -139 А-В = 861 Дополнительный код отрицательных чисел является математическим дополнением абсолютной величины числа до основания r системы счисления для дробных чисел и до rn для целых чисел.
где Положительные числа в дополнительном коде не меняют своего изображения. Правило преобразования числа в дополнительный код можно записать:
Рассмотрим несколько примеров сложения чисел в дополнительных кодах. А= 0,1001 [A]доп = 0,1001 А= - 0,1001 [A]доп = 1,0111 В= - 0,0100 [B]доп = 1,1100 В= 0,0100 [B]доп = 0,0100 10,0101 1,1011 Теорема. Сумма дополнительных кодов чисел есть дополнительный код результата. Доказательство теоремы приведено в [1]. Теорема справедлива для всех случаев, в которых не возникает переполнения разрядной сетки, что позволяет складывать машинные представления чисел по правилам двоичной арифметики, не разделяя знаковую и значащую части числа. Для выполнения арифметических операций над числами в дополнительном коде используется двоичный сумматор дополнительного кода, характерной особенностью которого является наличие поразрядного переноса из старшего значащего в знаковый разряд. Обратный код числа. Обратный код двоичного числа является инверсным изображением числа, в котором все разряды исходного числа принимают инверсное (обратное) значение. Правила преобразования чисел в обратный код аналитически можно определить следующим образом:
Выполнение арифметических операций над числами в обратном коде осуществляется на сумматоре обратного кода. Этот код имеет несущественный недостаток: требует наличия в сумматоре цепи циклического переноса из знакового разряда в младший значащий. Это может привести к увеличению времени выполнения арифметических операций. Ниже приведены несколько примеров выполнения арифметических операций над числами, записанными в обратном коде.
А= 0,1001 [A]обр = 0,1001 А= - 0,1001 [A]обр = 1,0110 В= - 0,0100 [B]обр = 1,1011 В= 0,0100 [B]обр = 0,0100
0,0101 Теорема. Сумма обратных кодов чисел есть обратный код результата. Доказательство теоремы приведено в [1].
Модифицированные коды Для обнаружения переполнения разрядной сетки можно использовать модифицированные коды. Модифицированные коды отличаются от обычных кодов тем, что знак числа кодируется двумя разрядами. При выполнении алгебраического сложения или вычитания два знаковых разряда участвуют в операции как равноправные цифровые разряды. После выполнения операции содержимое знаковых разрядов определяет знак результата (левый знаковый разряд) и наличие переполнения (несовпадение знаковых разрядов): комбинация 01 фиксирует переполнение при сложении положительных чисел (положительное переполнение), а 10 – отрицательных (отрицательное переполнение).
А=+0,101 [A] моддоп = 00,101 B=+0,110 [B] моддоп = 00,110 [A]моддоп+[B] моддоп = 01,011
А=-0,101 [A] моддоп = 11,011 B=-0,110 [B] моддоп = 11,010 [A]моддоп+[B] моддоп = 10,101
Логическая схема формирования единичного сигнала при возникновении переполнения приведена на рис 2.
Округление Речь идет об округлении только дробных чисел, целые не округляются. Так как в ЭВМ используются числа с конечным числом разрядов, а также часто выполняются операции приведения данных одной размерности к данным другой, то операция округления выполняется достаточно часто. В общем виде число с плавающей запятой, размещенное в разрядной сетке размерностью k, имеет вид Ar=mark. Если для записи мантиссы используются только n разрядов, то число может быть представлено в виде двух частей: Ar=[ma]rn+[A0]rk-n, где [A0]rk-n=A0 – часть числа, не вошедшая в разрядную сетку размерностью k. В зависимости от того, как учитывается А0 при записи числа А в n–раз-рядную сетку, можно выделить несколько способов округления чисел. 1. Отбрасывание А0. При этом возникает относительная погрешность õокр=|А0|rk-n/(|mA|rn), так как r -1≤ |mA| <1, 0≤ |A0| <1, то õокр=r--(n-1). 2. Симметричное округление. При этом производится анализ величины А0:
При условии |А0|≥r-1 единица добавляется к младшему разряду мантиссы. Данный способ округления наиболее часто используется на практике. 3. Округление по дополнению. В этом случае для округления используется (n+1)-й разряд. Если в нем находится единица, то она передается в n-й разряд, иначе разряды начиная с (n+1)-го отбрасываются. 4. Случайное округление. Генератор случайных чисел формирует нулевое или единичное значение, посылаемое в младший разряд мантиссы. Оценка точности вычислений зависит как от вида выполняемых операций, так и от последовательности их следования друг за другом. Нормализация чисел Число называется нормализованным, если его мантисса удовлетворяет условию r -1 ≤ |MA|<1. Нормализация – процесс, относящийся к числам, записанным в форме с плавающей запятой. Число A =0,00101…1 – денормализованное (признак нарушения нормализации вправо). Для нормализации число нужно сдвинуть в сторону, противоположную направлению нарушения нормализации. Таким образом, в примере мантиссу числа А необходимо сдвинуть влево на два разряда. При этом порядок необходимо уменьшить на два. Различают два вида сдвигов: простой и модифицированный. Простой сдвиг – сдвиг, выполняемый по правилу:
Модифицированный сдвиг - сдвиг, при котором в сдвигаемый разряд заносится значение, совпадающее со значением знакового разряда.
Нарушение нормализации вправо может быть более глубоким при вычитании, например, одного числа из другого, если они близки по величине. ...
Тс(пар) @ ntлэ . Очевидно, Tc(посл) ≤ Тс(пар), так как
где k - коэффициент запаса, обеспечивающий полное окончание всех переходных процессов в сумматоре последовательного действия k Î [1,2, 1,3]. Недостатком такого параллельного суммирования является большое время распространения сигналов переноса Pi. Параллельные безрегистровые сумматоры обеспечивают наибольшую скорость суммирования, если снабжены схемой ускоренного переноса.
Матричные методы умножения Кроме рассмотренных методов ускоренного умножения существуют методы умножения, основанные на использовании матриц промежуточных результатов. Пусть имеем сомножители: Мн = А = аn ... a2 a1
Рассмотрим схему умножения чисел согласно алгоритму Б. Данная схема умножения может быть представлена в виде матрицы (табл.3).
Для суммирования по столбцам могут быть использованы счетчики. Однако при достаточно большом значении величины n потребуются счетчики с большим числом входов, что существенно увеличит время сложения. Но этот принцип умножения может быть реализован на устройствах, имеющих не более трех входов. В качестве их могут быть использованы одноразрядные двоичные сумматоры и полусумматоры. На рис. 10 приведена структурная схема устройства умножения для реализации матричного алгоритма. Реализация методов матричного умножения требует большего количества оборудования, чем метод последовательного умножения, и дает больший выигрыш во времени. В связи с увеличением степени интеграции элементной базы ограничения по количеству оборудования становятся не столь строгими.
Машинные методы деления Деление - простое многократное вычитание делителя вначале из делимого, затем из остатков. Введем обозначения, используемые ниже: Дм - делимое, Дт - делитель, Аi – очередной (i-й) остаток, Чт – частное. Известны два основных подхода к операции деления: § с восстановлением остатков; § без восстановления остатков. Независимо от метода деления после каждого вычитания делителя формируется цифра частного. Операция деления является операцией, дающей не всегда точный результат. Поэтому признаком окончания операции деления может быть достижение заданной точности (по числу сдвиговых сигналов). Если при выполнении деления получен нулевой i-й остаток, то деление прекращается и в оставшиеся разряды частного записываются нули. Первым шагом деления двух чисел машиной является пробное вычитание, выявляющее соотношение между делимым и делителем. При делении в случае переполнения следует: для чисел с фиксированной запятой процесс остановить, с плавающей запятой продолжить до конца, а потом, после получения последней n-й цифры частного, число сдвигается вправо на один разряд с добавлением единицы к порядку, равному разности порядков делимого и делителя. Методы ускорения деления Логические методы основываются на анализе остатка, по виду которого можно сформировать несколько цифр частного в пределах одного такта. При этом Дт выбирается (формируется) таким образом, чтобы после запятой шла единица, то есть он нормализован. Если очередной остаток получился настолько мал, что после запятой следует r+1 нулей, то в частное может быть записано r ”0” или ”1”, а остаток может быть сдвинут на r разрядов влево. Итак, для осуществления названных методов ускорения кроме устройства управления делением требуется логическая схема, осуществляющая две функции: 1) сдвиг модулей делителя и делимого до тех пор, пока у модуля делителя после запятой не останется ни одного нуля; 2) выявление остатков вида 0,0…01 или 1,1…10. Степень сложности логической схемы определяется количеством разрядов, участвующих в косвенном сравнении модулей делителя и делимого (остатков). Обычно реализация логических методов ускорения при делении несколько сложнее, чем при умножении. При делении необходимо либо каждый остаток переводить в прямой код, либо, если остаток оставить в дополнительном коде, анализировать два разряда одновременно 0,0… или 1,1….
Двоично-десятичные коды Пусть число A представлено в системе счисления с основанием r:
Цифры ai будем представлять двоичными разрядами d1,d2,…,dm. Каждому двоичному разряду припишем веса p1,p2,…,pm. Тогда каждый разряд ai числа A будет иметь вид
где n и m определяют общее число двоичных разрядов. Если каждый разряд числа имеет вес и при r≠2k не выполняется равенство pk=r ∙ pk-1, то системы принято называть взвешенными. Количество разрядов m должно удовлетворять выражению m ≥ log2r. Если десятичное число записано в виде (4), то будем говорить, что число представлено в двоично-десятичном коде. Наибольшее распространение из них получили коды, в которых десятичная цифра представляется двоичной тетрадой (BCD-коды). Существует множество способов кодирования десятичных цифр. Существенным при этом является простота представления инверсных кодов и простота выделения (формирования) сигнала переноса из цифры в цифру. Сформулируем набор требований, позволяющих упростить выполнение арифметических операций и операций перевода чисел. § Четность, состоит в том, что четным десятичным цифрам соответствуют только четные двоичные коды и наоборот. Это обеспечивает эффективность операций округления, умножения и деления чисел в BCD-кодах. § Дополняемость, заключается в том, что сумма двоичного кода и инверсного ему кода любой десятичной цифры должна быть равна 9. Это обеспечивает эффективность операции алгебраического сложения в BCD-кодах. § Упорядоченность, то есть большей десятичной цифре соответствует большая тетрада и наоборот. § Единственность представления десятичной цифры двоичной тетрадой. § Взвешенность, то есть каждому разряду двоичного представления десятичной цифры поставлен в соответствие вес. Это обеспечивает эффективность всех арифметических и логических операций в BCD-кодах. Если каждая десятичная цифра кодируется соответствующим двоичным эквивалентом, то такое кодирование называется кодом прямого замещения. BCD-код – код, взаимодополняемый до 15. Это создает некоторые неудобства при суммировании чисел - ввод поправки в некоторых случаях. В то же время этот код имеет одно существенное достоинство – аддитивность: сумма кодов равна коду суммы. 0011 код 3 0101 код 5
Основной недостаток этого кода заключается в том, что инверсия какой- либо цифры оказывается цифрой, дополняющей данную цифру до 15, а не до 9. a = 0100
В табл. 4 показаны различные способы кодирования десятичных цифр. Таблица 4
BCD-коды с избытком 3 Иначе говоря, это коды чисел из системы (BCD + 3). В этом коде каждая десятичная цифра ai представляется в виде двоичного эквивалента суммы ai+3. В отличие от BCD-кода код BCD+3 – самодополняющийся, но не имеющий свойства взвешенности. Применяется наиболее часто в десятичной арифметике, так как при выполнении двоичного суммирования легко выделить десятичный перенос. Возможны следующие два случая сложения чисел в BCD-коде +3: 1) a + b ≤ 9; [ (a + 3) + (b + 3) ] ≤ 15. И, следовательно, в тетраде суммы будут лишние 6 единиц. Чтобы тетрада суммы осталась тоже с избытком 3, нужно вычесть 3. 2) a + b ≥ 10; [ (a + 3) + (b + 3) ] ≥ 16. Здесь во всех случаях возникает шестнадцатеричный перенос, вместе с которым тетраду суммы покинут и шесть избыточных единиц; чтобы тетрада суммы осталась с избытком 3, надо добавить 3. Если складываются числа с разными знаками, то избыток в тетраде суммы будет равен нулю и суммирование, таким образом, сводится к правилам суммирования в BCD-коде. Пример. Выполнить сложение чисел 169 и 378 в BCD-коде +3. 0.0100 1001 1100 A = 169 0.0110 1010 1011 B = 378 0.1011 0100 0111 A + B = 547 -0011+0011+0011 0.1000 0111 1010 8 7 10 Пример. Выполнить вычитание из числа 378 числа 169 в BCD-коде +3. A = 378 0.0110 1010 1011 B = 1691.1011 0110 0011 A - B = 209 1 0.0010 0000 1110
+ 0011 -0011 -0011 0.0101 0011 1100 5 3 12 Пример. Выполнить вычитание из числа 169 числа 378 в BCD-коде +3. A = 169 0.0100 1001 1100 B = 3781.1001 0101 0100 A - B = -209 1.1101 1111 0000 -0011 -0011 +1100 1.1010 1100 0011 - 0101 0011 1100 5 3 12 Правило. Если из тетрады был перенос, надо добавить +0011, если переноса не было, – 0011 (добавить 1100), независимо от знака слагаемых и знака суммы.
Коды Хемминга Американский ученый Р. Хемминг предложил способ кодирования информации, позволяющий не только обнаруживать, но и исправлять ошибки при передаче одиночного слова любой разрядности. Эти коды – систематические. Пусть разрядность слова равна m. Для контроля информации требуется k дополнительных разрядов. Число k выбирается согласно следующим правилам. 1. Контролирующее число k выбирается так, чтобы оно имело количество комбинаций, достаточное для распознавания одной из m+k позиций или для сигнализации отсутствия ошибки. Полученное таким образом число описывает n=m+k+1 событий. Следовательно, необходимо, чтобы выполнялось неравенство 2k≥(m+n+1). 2. (m+k)-разрядные позиции нумеруются от единицы до (m+k), начиная от младшей значащей. Контрольные разряды k обозначаются P0, P1, P2, …,Pk-1 и помещаются в разряды, имеющие номера 1,2,4,8, …,2k-1 (m+k)-разрядного числа. Остальные m разрядов могут быть размещены в любом порядке между контрольными разрядами. 3. Контрольные разряды P0, P1, P2, …,Pk-1 выбраны таким образом, чтобы для определенных разрядов слова служить в качестве контрольных избыточных разрядов.
P0 выбрано с таким расчетом, чтобы в позициях 1, 3, 5, 7, 9, 11 … число единиц каждого слова было четным, P1 выбрано для того, чтобы выполнялось условие четности в разрядах 2, 3, 6, 7, 10, 11, 14, 15 …, аналогично P2 контролирует позиции 4,5,6,7,12,13,14,15,20… и P3 − для разрядов 8, 9,10,11,12,13, 14,15,24,25…. На основании рассмотренных правил в табл. 6 показаны семиразрядные коды. Контрольные разряды обозначены P0, P1 и P2 и помещены в позициях 1, 2 и 4. Операция обнаружения и исправления ошибок выполняется путем нахождения k-разрядного контрольного числа. При этом младший значащий разряд контрольного числа находится посредством проведения контроля на четность над разрядами 1,3,5,7,9…. Если контроль показывает правильность передачи, то пишется нуль, иначе − единица. Следующий разряд контрольного числа Таблица 6
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1400; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.191.169 (0.201 с.) |
 , (2)
, (2) ai r1i =
ai r1i = 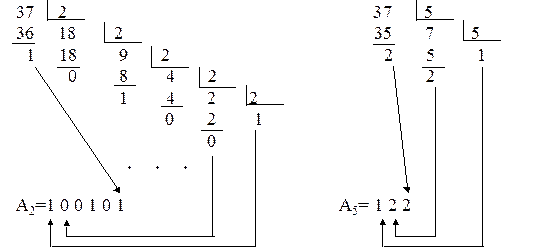


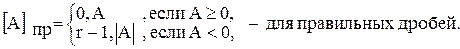
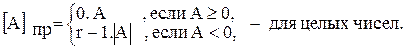
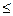 [A]пр
[A]пр  1 - младший разряд дополняется до основания системы счисления
1 - младший разряд дополняется до основания системы счисления A2 '=24 - А=10000 - 1011 = 0101, или А2' = 0101
A2 '=24 - А=10000 - 1011 = 0101, или А2' = 0101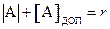 - для дробных чисел,
- для дробных чисел,  - для целых чисел,
- для целых чисел,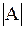 - абсолютное значение числа А, n – число цифр числа.
- абсолютное значение числа А, n – число цифр числа.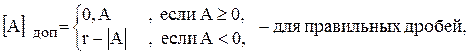
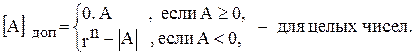
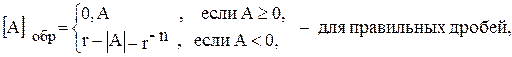 ,
,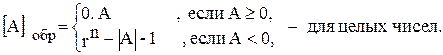 .
. 10,0100 1,1010
10,0100 1,1010 1
1
 Функция переполнения имеет вид: f=Зн1 Зн2 + Зн1 Зн2 = Зн1 Å Зн2.
Функция переполнения имеет вид: f=Зн1 Зн2 + Зн1 Зн2 = Зн1 Å Зн2.



 yn y2 y1
yn y2 y1









 P P P
P P P

 Рис. 4. Схема параллельного суммирования
Рис. 4. Схема параллельного суммирования
 t @ (3,6) ktлэ,
t @ (3,6) ktлэ, Мт = B = bn... b2 b1
Мт = B = bn... b2 b1
 Каждый элемент ai bj (i, j = 1, n) принимает значение 0 или 1. Произведение A∙B может быть получено, если суммировать элементы матрицы (по диагонали).
Каждый элемент ai bj (i, j = 1, n) принимает значение 0 или 1. Произведение A∙B может быть получено, если суммировать элементы матрицы (по диагонали).
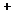



 , а все число
, а все число , (4)
, (4) 1000 код 8
1000 код 8

 a = 1011
a = 1011  циклический перенос 1
циклический перенос 1 0.0010 0000 1111
0.0010 0000 1111


