
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 11. Определение натуральной величины отрезка прямой и плоской фигуры методом вращения.
Натуральную величину плоской фигуры удобнее находить с помощью вращения вокруг прямой уровня. Путем такого вращения плоскость, которой принадлежит рассматриваемая фигура, поворачивают в положение, параллельное плоскости проекций. При таком положении плоскости любая принадлежащая ей фигура будет проецироваться в натуральную величину. Вопрос 12. Кривые линии. Порядок кривой. Кривые линии второго порядка: эллипс, парабола, гипербола - определения и правила построения. Все кривые линии можно разделить на плоские и пространственные. Все множество плоских кривых можно разделить на циркульные и лекальные. Циркульной называют кривую, которую можно построить с помощью циркуля. К ним относятся окружность, овал, завиток и т.д. Лекальной называют кривую, которую нельзя построить с помощью циркуля. Ее строят по точкам с помощью специального инструмента, называемого лекалом. К лекальным кривым относятся эллипс, парабола, гипербола, спираль Архимеда и др.
Другой вариант построения эллипса по двум осям разобран на рис.2.9. При построении проводим окружности радиусами r и R из одного центра О и произвольную секущую ОА. Из точек пересечения 1 и 2 проводим прямые, параллельные осям эллипса. На их пересечении отмечаем точку М эллипса. Остальные точки строим аналогично.
Гипербола - кривая второго порядка, разность расстояний от любой точки которой до двух фокусов есть величина постоянная, равная действительной оси гиперболы. Вдоль действительной оси расположены ветви гиперболы. Гиперболу по величине действительной оси и двум фокусам строим в следующей последовательности (рис.2.11). На оси гиперболы откладываем произвольный отрезок АК. Проводим две окружности с центрами в F 1 и F 2 радиусом r 1 = АК и две окружности радиусом r 2 = ВК. Точки 1, 2, 3, 4 пересечения окружностей принадлежат гиперболе. Пространственные кривые. Цилиндрическая винтовая линия
Для построения конической винтовой линии (рис.2.14) изобразим некоторое число положений прямой, равномерно отстоящих друг от друга (в данном случае 12). Положение точки, движущейся вдоль прямой, будем фиксировать так, чтобы движение вдоль прямой было пропорционально угловому перемещению вокруг оси. Горизонтальной проекцией конической винтовой линии будет спираль Архимеда. Фронтальной проекцией - синусоида с затухающей амплитудой. Получили левую винтовую линию.
|
||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 98; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.19.56.114 (0.005 с.) |
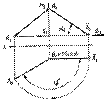 Вращение вокруг проецирующей прямой применяют при решении задачи на определение натуральной величины отрезка прямой (рис.6.2). Ось вращения выбирают так, чтобы она проходила через одну из крайних точек отрезка, например, через точку В. Тогда при повороте точки А на угол j в положение А отрезок АВ перемещается в положение АВ, параллельное плоскости П 2. В этом случае отрезок будет проецироваться на П 2 в натуральную величину (½ В 2 А 2 ½= ½ ВА ½). Одновременно в натуральную величину будет проецироваться угол а наклона отрезка АВ к плоскости П 1.
Вращение вокруг проецирующей прямой применяют при решении задачи на определение натуральной величины отрезка прямой (рис.6.2). Ось вращения выбирают так, чтобы она проходила через одну из крайних точек отрезка, например, через точку В. Тогда при повороте точки А на угол j в положение А отрезок АВ перемещается в положение АВ, параллельное плоскости П 2. В этом случае отрезок будет проецироваться на П 2 в натуральную величину (½ В 2 А 2 ½= ½ ВА ½). Одновременно в натуральную величину будет проецироваться угол а наклона отрезка АВ к плоскости П 1.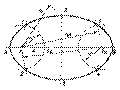 Эллипс - кривая второго порядка, сумма расстояний от любой точки которой до двух фиксированных точек, называемых фокусами, есть величина постоянная, равная большой оси эллипса.
Эллипс - кривая второго порядка, сумма расстояний от любой точки которой до двух фиксированных точек, называемых фокусами, есть величина постоянная, равная большой оси эллипса.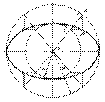 Один из вариантов построения эллипса по большой оси АВ и двум фокусам F 1 и F 2 приведен на рис.2.8. На большой оси эллипса откладываем произвольный отрезок АК, но больший отрезка AF 1. Радиусом r 1 = АК проводим окружности с центрами F 1 и F 2. Затем радиусом r 2 = ВК проводим окружности, также с центрами F 1 и F 2. Точки 1, 2, 3, 4 пересечения больших и малых окружностей принадлежат эллипсу, так как они удовлетворяют определению эллипса.
Один из вариантов построения эллипса по большой оси АВ и двум фокусам F 1 и F 2 приведен на рис.2.8. На большой оси эллипса откладываем произвольный отрезок АК, но больший отрезка AF 1. Радиусом r 1 = АК проводим окружности с центрами F 1 и F 2. Затем радиусом r 2 = ВК проводим окружности, также с центрами F 1 и F 2. Точки 1, 2, 3, 4 пересечения больших и малых окружностей принадлежат эллипсу, так как они удовлетворяют определению эллипса. Парабола - кривая второго порядка, расстояние от любой точки которой до фокуса равно расстоянию от этой точки до некоторой фиксированной прямой, называемой директрисой.
Парабола - кривая второго порядка, расстояние от любой точки которой до фокуса равно расстоянию от этой точки до некоторой фиксированной прямой, называемой директрисой.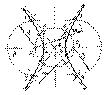 На рис.2.10 приведен пример построения параболы по директрисе 1 и фокусу F. Вершина параболы (точка А) находится на середине отрезка OF. Далее от точки О вдоль оси параболы откладываем произвольный отрезок ОК, который должен быть больше ОА. Через точку К проводим прямую а, перпендикулярную оси параболы. Из фокуса радиусом r = ОК строим окружность. Точки 1 и 2 пересечения окружности и прямой а принадлежат параболе. Аналогично строим необходимое количество точек.
На рис.2.10 приведен пример построения параболы по директрисе 1 и фокусу F. Вершина параболы (точка А) находится на середине отрезка OF. Далее от точки О вдоль оси параболы откладываем произвольный отрезок ОК, который должен быть больше ОА. Через точку К проводим прямую а, перпендикулярную оси параболы. Из фокуса радиусом r = ОК строим окружность. Точки 1 и 2 пересечения окружности и прямой а принадлежат параболе. Аналогично строим необходимое количество точек. Пусть точка А (рис.2.12) равномерно движется по прямой 1, прямая, в свою очередь, равномерно вращается вокруг оси i, ей параллельной. При вращении прямая 1 образует цилиндрическую поверхность, а точка А опишет пространственную кривую, которую называют цилиндрической винтовой линией или гелисой (геликой). Расстояние от точки А до оси i называют радиусом винтовой линии, а расстояние между точками А1 и АVIII, лежащими на одной прямой - шагом винтовой линии.
Пусть точка А (рис.2.12) равномерно движется по прямой 1, прямая, в свою очередь, равномерно вращается вокруг оси i, ей параллельной. При вращении прямая 1 образует цилиндрическую поверхность, а точка А опишет пространственную кривую, которую называют цилиндрической винтовой линией или гелисой (геликой). Расстояние от точки А до оси i называют радиусом винтовой линии, а расстояние между точками А1 и АVIII, лежащими на одной прямой - шагом винтовой линии.
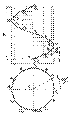 Построим комплексный чертеж винтовой линии по ее радиусу R и шагу р (рис.2.13). Примем ось винтовой линии i, расположенной перпендикулярно горизонтальной плоскости проекций П 1. Все точки винтовой линии отстоят от оси на одинаковом расстоянии, поэтому горизонтальной проекцией этой линии будет окружность радиуса R с центром на оси L. Выберем начальную точку винтовой линии - точку 1. Разделим окружность на 12 равных частей и примем полученные точки за горизонтальные проекции точек, принадлежащих винтовой линии. По условию задачи шаг винтовой линии равен р, следовательно, при переходе точки 1 в положение 2 она поднимется на высоту, равную 1/12 р, при переходе в положение 3 - на высоту 2/12 р и т.д. Поделив шаг на 12 частей, построим фронтальные проекции точек, принадлежащих винтовой линии.
Построим комплексный чертеж винтовой линии по ее радиусу R и шагу р (рис.2.13). Примем ось винтовой линии i, расположенной перпендикулярно горизонтальной плоскости проекций П 1. Все точки винтовой линии отстоят от оси на одинаковом расстоянии, поэтому горизонтальной проекцией этой линии будет окружность радиуса R с центром на оси L. Выберем начальную точку винтовой линии - точку 1. Разделим окружность на 12 равных частей и примем полученные точки за горизонтальные проекции точек, принадлежащих винтовой линии. По условию задачи шаг винтовой линии равен р, следовательно, при переходе точки 1 в положение 2 она поднимется на высоту, равную 1/12 р, при переходе в положение 3 - на высоту 2/12 р и т.д. Поделив шаг на 12 частей, построим фронтальные проекции точек, принадлежащих винтовой линии. 


