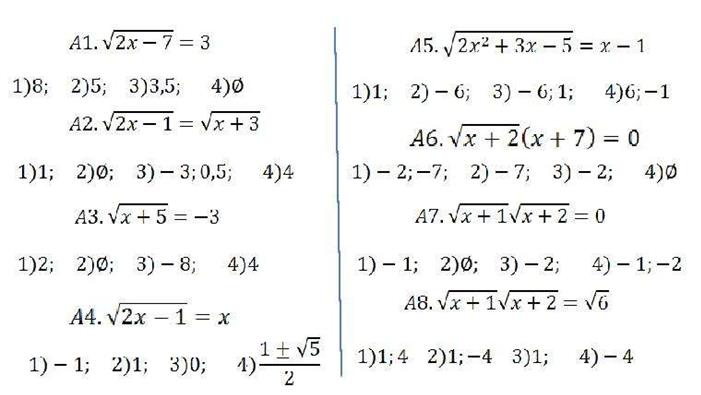Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема. Решение иррациональных уравненийСтр 1 из 3Следующая ⇒
Тема. Решение иррациональных уравнений Вопросы темы: Методы решения иррациональных уравнений: Метод пристального взгляда. Метод возведения обеих частей уравнений в одну и ту же степень. Решение уравнений с использованием замены переменной. Метод разложения на множители выражений, входящих в уравнение. Метод выделения полных квадратов при решении иррациональных уравнений. Метод оценки. Иррациональные уравнения, содержащие степени выше второй. ДОМАШНЕЕ ЗАДАНИЕ Методы решения иррациональных уравнений
Определение: Уравнение с одной переменной называют иррациональным, если хотя бы одна из функций
При решении иррациональных уравнений необходимо установить: - область допустимых значений переменных, исходя из условия, что все радикалы, входящие в уравнение, должны быть арифметическими.
Метод пристального взгляда
Этот метод основан на следующем теоретическом положении: “Если функция Для реализации метода, основанного на этом утверждении требуется: а) Выделить функцию, которая фигурирует в уравнении. b) Записать область определения данной функции. c) Доказать ее монотонность (возрастание) в области определения. d) Угадать корень уравнения. t) Обосновать, что других корней нет. f) Записать ответ. Пример 1. Наличие радикалов четной степени говорит о том, что подкоренные выражения должны быть неотрицательными. Поэтому сначала найдем область допустимых значение переменной
Очевидно, что левая часть уравнения не существует ни при одном значении неизвестного Таким образом, вопрос о решении уравнения снимается – ведь нельзя же осуществить операцию сложения в левой части уравнения, так как не существует сама сумма. Каков же вывод? Уравнение не может иметь решений, так как левая часть не существует ни при одном значении неизвестного Пример 2: Рассмотрим функцию Найдем область определения данной функции:
Данная функция является монотонно возрастающей.
Для
Число 5 принадлежит области значения, следовательно, согласно утверждению Проверкой убеждаемся, что это действительный корень уравнения.
Метод возведения обеих частей уравнений в одну и ту же степень. Теорема. Пример 1.
Ответ: Если в уравнение входят несколько радикалов, то их можно последовательно исключать с помощью возведения в квадрат, получая в итоге уравнение вида При этом полезно учитывать область допустимых значений исходного уравнения. Пример 2.
Ответ: Входящих в уравнение. Теорема. Уравнение
Пример 1.
При Ответ: Выделить общий множитель часто бывает очень трудно. Иногда это удается сделать после дополнительных преобразований. В приведенном ниже примере для этого рассматриваются попарные разности подкоренных выражений. Пример 2.
Если внимательно посмотреть на уравнение, то можно увидеть, что разности подкоренных выражений первого и третьего, а также второго и четвертого членов этого уравнения равны одной и той же величине В таком случае далее следует воспользоваться тождеством:
Уравнение примет вид:
Корень уравнения Уравнение Ответ: Метод оценки. Этот способ применим в том случае, когда подкоренные выражения представляют собой квадратный трехчлен, не раскладывающийся на линейные множители. Поэтому целесообразно оценить левую и правую части уравнения. Пример 1.
Оценим обе части уравнения:
Левая часть уравнения существует при всех значениях переменной а правая – при всех значениях, не больших 5, следовательно, уравнение будет иметь решение, если обе части уравнения одновременно равны 5, т. е. справедлива следующая система:
Корнем второго уравнения системы является число Проверим, является ли это число корнем второго уравнения:
Ответ: Пример 2.
Для всех
Используя неравенство Коши, можем записать:
причем равенство достигается при Таким образом, Ответ: Выше второй.
Если уравнение имеет вид - при нечетном - а при четном Пример 1
Возведем обе части уравнения в куб:
которое равносильно совокупности двух уравнений:
Ответ: При решении иррациональных уравнений очень часто пользуются следующим приемом. Если В последнем равенстве Далее легко избавиться от кубической иррациональности, возводя обе части в куб. Пример 2.
Здесь, очевидно, Возведем в куб обе части уравнения, получим:
или
или
или
или Ответ: Замечание. Замена в конкретном примере левой части на правую, вообще говоря, неправомерна – ведь нам неизвестно ни одно значение От того, что школьник решит лишний десяток задач, умнее и сообразительнее он не станет, Результат обучения оценивается не количеством сообщаемой информации, а качеством ее усвоения. Это качество будет выше, если на один и тот же пример посмотреть с разных сторон. Решение задач разными способами способствует развитию активного мышления учащихся. Хорошую почву для этого дает решение примеров разными способами. Пример 3. Способ 1.
Возведем обе части уравнения в куб:
Группируя, получаем:
Используя равенство (1) имеем:
или
или
или
Ответ: Способ 2. Иногда полезно ввести не одну вспомогательную переменную, а несколько, сводя исходное уравнение к системе уравнений.
Пусть Таким образом справедлива следующая система:
Возвращаясь к переменной Ответ: В следующем примере введение вспомогательной переменной сводит исходное уравнение к однородному. Пример 4.
Положим Тогда исходное уравнение примет вид:
Поскольку
Осталось решить уравнения Корнями этих уравнений являются числа
Ответ: Пример 5.
Область допустимых значений задается неравенством Преобразуем уравнение следующим образом:
Один корень этого уравнения Для решения второго уравнения положим и решим Корни этого уравнения Последний корень не принадлежит указанному промежутку, поэтому, решая уравнение
Ответ:
ДОМАШНЕЕ ЗАДАНИЕ
1. Представленный материал изучить и законспектировать в тетрадь по математике. 2. Обязательным к изучению являются методы, представленные в вопросах 1, 2 и 3. 3. Материал, представленный в вопросах 1, 4, 5, 6, 7 – для желающих выучить дополнительный материал. 4. Выполнить примеры домашнего задания в тетради по математике: Примеры задания: 1. Решить представленные уравнения: А1 – А8. 2. Сверить свой ответ с представленными ответами.
Тема. Решение иррациональных уравнений Вопросы темы: Методы решения иррациональных уравнений: Метод пристального взгляда.
|
|||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 75; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.12.209 (0.076 с.) |
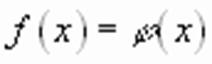
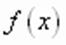 или
или 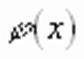 содержит переменную под знаком радикала.
содержит переменную под знаком радикала.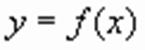 возрастает в области определения и число
возрастает в области определения и число 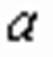 входит в множество значений, то уравнение
входит в множество значений, то уравнение 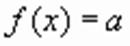 имеет единственное решение.”
имеет единственное решение.”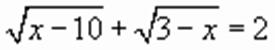 .
.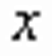 .
.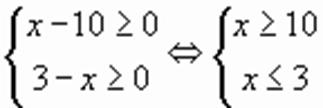
 .
.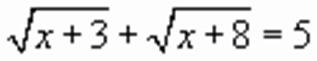
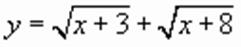 .
.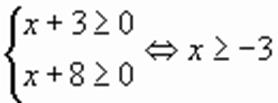
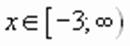 эта функция будет принимать наименьшее значение при
эта функция будет принимать наименьшее значение при 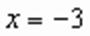 , а далее только возрастать.
, а далее только возрастать.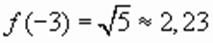 .
.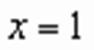 .
.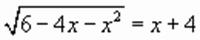
 ,
,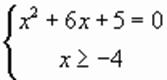 ,
,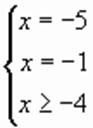 .
.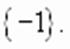

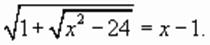

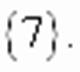
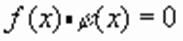 , определенное на всей числовой оси, равносильно совокупности уравнений
, определенное на всей числовой оси, равносильно совокупности уравнений 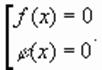
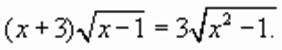
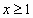 уравнение принимает вид:
уравнение принимает вид: 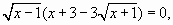 которое равносильно совокупности двух уравнений:
которое равносильно совокупности двух уравнений: 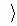
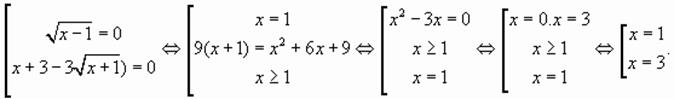
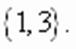

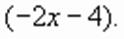

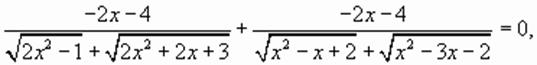 или
или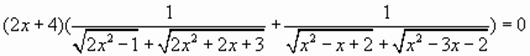
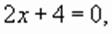 т.е. число
т.е. число  при подстановке в исходное уравнение дает верное равенство.
при подстановке в исходное уравнение дает верное равенство.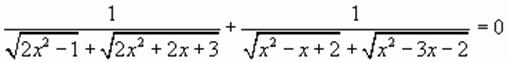 не имеет решений, так как его левая часть положительна в своей области определения.
не имеет решений, так как его левая часть положительна в своей области определения.
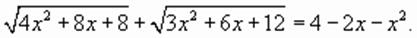
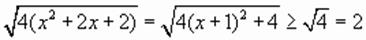 ,
,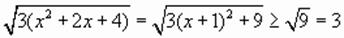 ,
,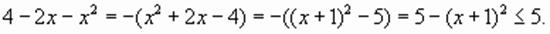
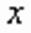 , не меньших 5,
, не меньших 5,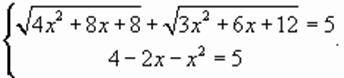
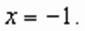
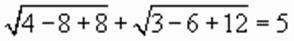 .
.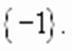
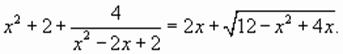
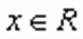 имеем
имеем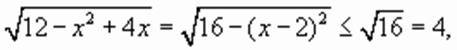
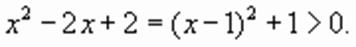
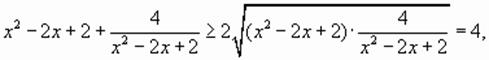
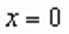 и
и 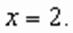
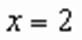 -корень исходного уравнения.
-корень исходного уравнения.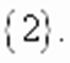
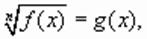 то его можно решить, возводя обе части этого уравнения в степень
то его можно решить, возводя обе части этого уравнения в степень 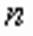 . Полученное уравнение
. Полученное уравнение 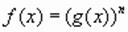 :
: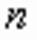 равносильно данному уравнению,
равносильно данному уравнению,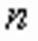 является его следствием, аналогично рассмотренному выше случаю при
является его следствием, аналогично рассмотренному выше случаю при 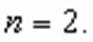
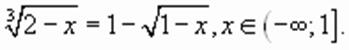
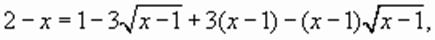 или
или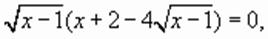
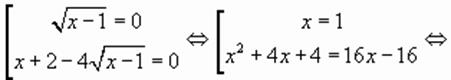
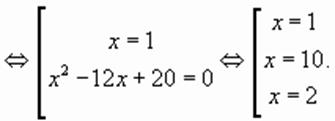
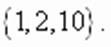
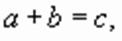 то
то 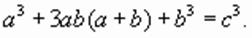
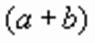 заменяем на
заменяем на 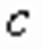 и получаем
и получаем 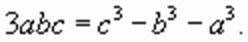
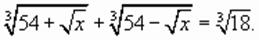
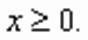
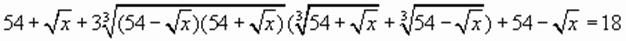 ,
,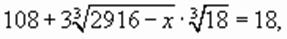
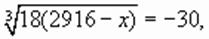
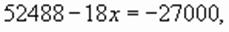
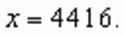 Проверка подтверждает, что это корень уравнения.
Проверка подтверждает, что это корень уравнения.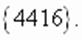
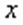 , при котором это уравнение превращается в верное числовое равенство. Возможно, таких решений нет вообще. Допуская в практических действиях такую замену, мы фактически расширяем возможное множество решений. Поэтому все найденные решения следует проверять и только те, которые превращают исходное уравнение в верное равенство, следует записать в ответ.
, при котором это уравнение превращается в верное числовое равенство. Возможно, таких решений нет вообще. Допуская в практических действиях такую замену, мы фактически расширяем возможное множество решений. Поэтому все найденные решения следует проверять и только те, которые превращают исходное уравнение в верное равенство, следует записать в ответ.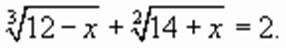 (1)
(1)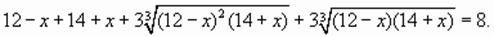
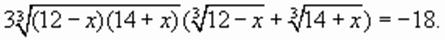
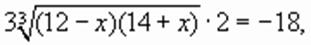
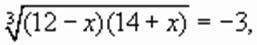
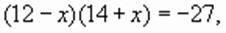
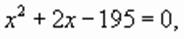 корни которого
корни которого 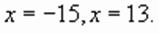
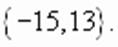
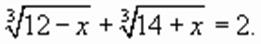
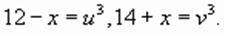 Тогда
Тогда 
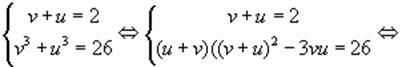
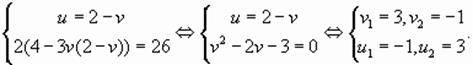
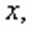 находим
находим 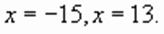
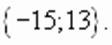
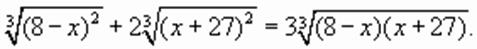
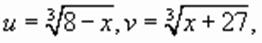
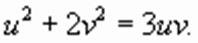
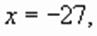 при котором переменная
при котором переменная 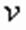 обращается в нуль, не является решением исходного уравнения (в чем можно убедиться подстановкой), делим обе части уравнения на
обращается в нуль, не является решением исходного уравнения (в чем можно убедиться подстановкой), делим обе части уравнения на 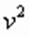
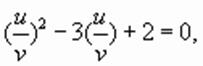 решая которое, находим:
решая которое, находим: 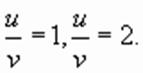
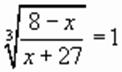 и
и 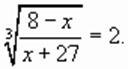
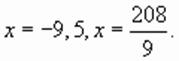
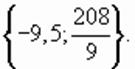
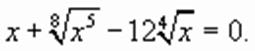
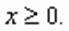
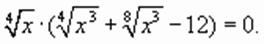
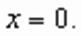
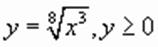
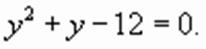
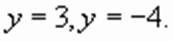
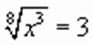 , получим
, получим