Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частотный критерий Михайлова
Как и при использовании критерия Гурвица исходной информацией для использования критерия Михайлова является характеристическое уравнение исследуемой системы (205). Здесь применяется геометрическая иллюстрация траектории движения конца вектора Михайлова – годограф Михайлова. На основе характеристического уравнения замкнутой системы (205) вводится в рассмотрение некоторая функция комплексного переменного, полученная заменой Функцию (210) можно представить в виде На комплексной плоскости В основе критерия Михайлова заложен принцип аргумента вектора (211). Характеристическое уравнение (205) представим в известном виде: Выражение (210) можно записать как Теперь (213) выразим через модуль и фазу (аргумент): где Проанализируем изменение составляющей аргумента Случай действительного отрицательного корня:
Рис. 74. Изменение положения В этом случае при изменении В случае пары комплексных сопряженных корней при изменении частоты Поведение вектора Суммарный угол поворота от пары комплексных корней при этом составит Следовательно, если все корни характеристического уравнения исследуемой системы лежат в левой полуплоскости, что соответствует устойчивой системе управления, то суммарный угол поворота вектора (214) при изменении частоты Очевидно, что если система находится на границе устойчивости, то для случая нулевого корня Для случая пары чисто мнимых корней поворот вектора где Поворот второго вектора Рассмотрим случай, когда замкнутая система неустойчива. В этом случае имеются корни, лежащие в правой полуплоскости. Если корень действительный
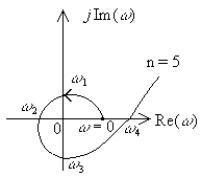
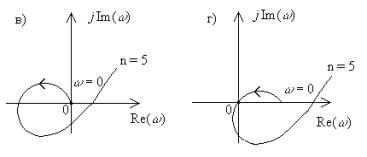
Следовательно, если m из n корней характеристического уравнения лежат в правой полуплоскости, то суммарный угол поворота вектора при изменении Определение. Для устойчивой системы управления n-го порядка необходимо и достаточно, чтобы годограф Михайлова при изменении На рис. 75 приведен годограф Михайлова для различных случаев.
Рис. 75. Примеры для случаев: а) устойчивой, Теперь обратимся к рис. 76, иллюстрирующему устойчивую САР. Для устойчивой САР наблюдается чередование корней действительной
Рис. 76. Изменение вещественной и мнимой составляющих Недостатком алгебраических критериев и частотного критерия устойчивости является их ограниченность системами без транспортного запаздывания. В случае системы с транспортным запаздыванием их применение дает приближенную оценку устойчивости в пределах правомерности аппроксимации звена транспортного запаздывания рядом Паде.
|
|||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 76; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.180.76 (0.009 с.) |
 :
: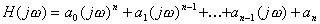 . (210)
. (210)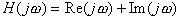 . (211)
. (211) вектор
вектор  опишет при изменении
опишет при изменении  от
от  до
до 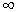 кривую – годограф Михайлова.
кривую – годограф Михайлова. . (212)
. (212) . (213)
. (213)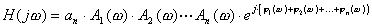 , (214)
, (214) . (215)
. (215)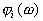 при
при  для случаев с различными типами корней
для случаев с различными типами корней  .
. . Поведение вектора
. Поведение вектора 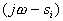 для этого случая показано на рис. 74, а.
для этого случая показано на рис. 74, а.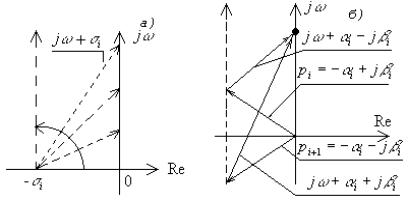
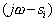
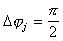 .
.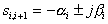
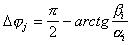 .
.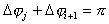 .
.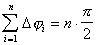 .
. при изменении
при изменении  .
.
 составит
составит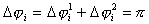 ,
, для
для 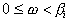 ,
, для
для 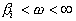 .
.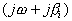 составит
составит .
.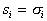 , вектор
, вектор 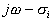 при изменении
при изменении  . Если пара комплексных сопряженных корней лежит в правой полуплоскости, то
. Если пара комплексных сопряженных корней лежит в правой полуплоскости, то .
. .
.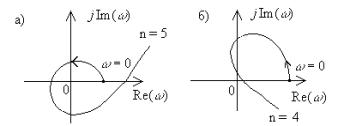
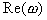 и мнимой
и мнимой 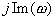 частей (следствие из критерия Михайлова).
частей (следствие из критерия Михайлова).