
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение метода молекулярной динамики для моделирования процесса диффузии
Диффузия обусловлена молекулярным движением частиц жидкости (газа). На макроскопическом уровне диффузия описывается законом Фика, согласно которому, поток j диффундирующих частиц, пропорционален градиенту концентрации частиц
где D – коэффициент диффузии; Рассмотрим моделирование процесса диффузии (самодиффузии), с позиций метода молекулярной динамики. Пусть в объеме жидкой фазы наносится возмущение индикатором, в виде δ-функции Дирака.
Реально, это означает, что в момент времени t = 0, в центре объема, был импульсно введен индикатор, с бесконечно высокой концентрацией. С макроскопической точки зрения, для описания эволюции частиц индикатора, необходимо привлечь закон сохранения массы частиц индикатора
и объединить его с законом Фика (17). Тогда получим
Решая уравнение (20) с начальным условием:
где δ(r) – дельта функция Дирака, получаем:
Здесь d – обозначает размерность системы. На самом деле, нас интересует применение метода молекулярной динамики, для оценки макроскопического параметра процесса молекулярной диффузии – коэффициента диффузии D. Попытаемся связать эволюцию распределения во времени концентрации индикатора, с коэффициентом диффузии D (макропараметром процесса). Если ввести понятие нормированной концентрации индикатора C (r, t), как:
то последняя будет являться функцией плотности распределения частиц индикатора по времени, на расстоянии r, от точки ввода индикатора (здесь C э (r, t) – размерная экспериментально замеряемая концентрация индикатора). Тогда справедливо следующее равенство:
где Умножим теперь левую и правую части уравнения (20) на r 2 и проинтегрируем по всему пространству:
Левая часть уравнения (25) равна: Применяя интегрирование по частям к правой части уравнения (25), получаем:
Уравнение (26) устанавливает связь между коэффициентом диффузии D и шириной профиля концентрации индикатора. Это соотношение впервые было получено Эйнштейном. Коэффициент диффузии D является макроскопическим коэффициентом переноса, а ‹ r 2 (t)› имеет микроскопическую интерпретацию: это средний квадрат расстояния, на которое сместились молекулы индикатора, за интервал времени t.
Это сразу же дает подсказку, как рассчитать D, методом молекулярной динамики. Надо для каждой частицы i рассчитать ее смещение Δ r i (t), за время t, и построить средний квадрат этих смещений, по всем частицам, в зависимости от времени t:
Тангенс угла наклона этой зависимости, при достаточно больших t, равен 2 dD.
|
|||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 75; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.74.44 (0.007 с.) |
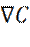 , этого типа, со знаком минус
, этого типа, со знаком минус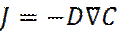 (17)
(17)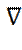 - оператор «набла» (соответствует градиенту).
- оператор «набла» (соответствует градиенту).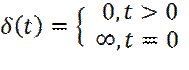 (18)
(18)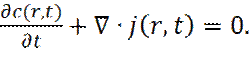 (19)
(19)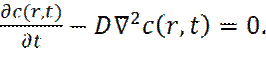 (20)
(20) (21)
(21) (22)
(22) (23)
(23)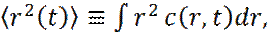 (24)
(24)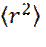 - математическое ожидание (среднее значение) квадрата радиуса, продиффундировавших частиц индикатора.
- математическое ожидание (среднее значение) квадрата радиуса, продиффундировавших частиц индикатора.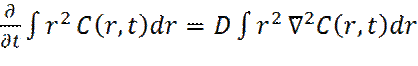 (25)
(25)
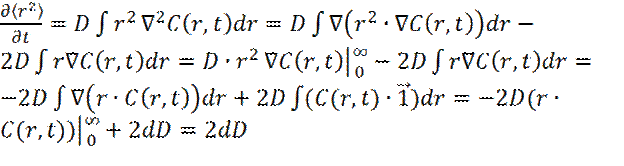 (26)
(26) (27)
(27)


