Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Циклы с известным числом повторений
Детерминированные циклы (циклы с известным числом повторений) – это такие циклы, для которых из постановки задачи понятно сколько раз будет по- вторяться тело цикла. Это может быть либо непосредственно известно, либо можно узнать путем несложных вычислений, используя исходные данные. На- пример, для обработки последовательности из n чисел тело цикла будет повто- ряться n раз. Для обработки последовательности на интервале от А до В с ша- гом h цикл будет выполняться [(А-В)/h]+1 раз.
Такой цикл называется еще «цикл с пара- метром». Для лаконичности можно использо- вать блок модификации, в котором задаются все параметры цикла: Этот блок еще называют заголовком цик- ла. Запись внутри блока читается как: «i изме- няется от А до В с шагом h». Если шаг равен 1, его можно не записывать. Использование цикла с постусловием для описания цикла с параметром не совсем корректно, так как если конечное зна- чение меньше начального, то цикл не выполнится ни разу. Поэтому правильнее использовать цикл с предусловием (рис. 15).
Циклы с параметром используются для решения многих прикладных задач, в частности: - для вычисления значения функции на заданном интервале, тогда в ка- честве счетчика цикла используется значение аргумента функции, изменяемое на заданном интервале;
- для вычислений по рекуррентным формулам, тогда в качестве счетчика цикла используется номер элемента последовательности, вычисляемого по этой формуле; - для работы с массивами данных, тогда в качестве счетчика цикла ис- пользуется номер элемента массива.
Вычисления на интервале. При исследовании функции или построении ее графика требуется вычислять значения функции при некоторых значениях ее аргумента. Для аргумента задается диапазон и шаг его изменения. Задача 10.
, при изменении значения аргумента на интервале [A,B] c шагом H, и определить, сколько значений аргумента (функции) при этом получится.
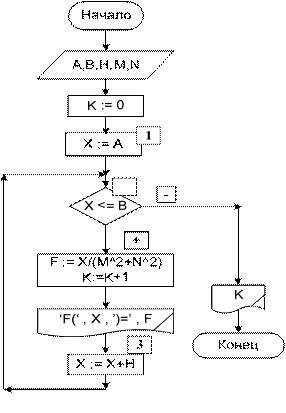
Исходные данные: A, B – соответственно начальное и конечное значение аргумента, т. е. левая и правая границы изменения аргумента; H– шаг измене- ния значения аргумента; M, N – параметры выражения (постоянные члены вы- ражения). Выходные данные: X – значение аргумента, F – значение функции, K – ко- личество значений аргумента (функции). Рабочие переменные: X – счетчик цикла, значение которого совпадает со значениями аргумента функции, K – счетчик значений аргумента (функции). Алгоритм решения этой задачи заключается в организации цикла, в кото- ром в качестве счетчика цикла выступает значение аргумента. Начальное зна- чение счетчика цикла – левая граница интервала, конечное значение – правая граница интервала. Для определения количества получаемых значений исполь- зуется счетчик. В блок-схеме 12 описан алгоритм решения этой задачи с ис- пользованием управляющей структуры цикла с предусловием. В блок-схеме 13 описан алгоритм решения этой же задачи, но с использованием блока модифи- кации (блок *), который заменяет блоки 1–3 блок-схемы 12. Комментарии к алгоритму. После блока ввода располагается блок подго- товки, в котором задается начальное значение счетчика значений аргумента (функции) – K. Очевидно, пока тело цикла не выполнено ни разу, то K равно нулю, т. е. аргумент функции еще не получал никакого значения и функция не вычислялась.
Переменная X выступает в двух ипостасях: как переменная (счетчик) цикла и как аргумент функции. Для организации цикла в блоке 1 она получает значение левой границы интервала. Затем проверяется условие продолжения цикла (блок 2). Если значение X не превысило конечное значение, т. е. правую границу интервала, то выполняется тело цикла, по окончании которого пере- менная X меняет свое значение, увеличиваясь на заданный шаг (блок 3).Если значение X превысило конечное значение, то тело цикла не выполняется и осу- ществляется выход из цикла. В теле цикла вычисляется значение функции по заданному выражению, считается количество повторений цикла (что то же самое количество получен- ных значений аргумента, и соответственно, количество полученных значений функции) и выводится значение аргумента и значение функции. После выхода из цикла выводится значение переменной K. В алгоритме решения задачи 10 имеется переменная – счетчик, предна- значенная для расчета количества получаемых значений. Такого рода перемен- ные часто встречаются в циклических алгоритмах. При повторении цикла про- исходит «накопление» значения переменной, реализуемое с помощью рекурсив- ных1 вычислений: переменная получает свое новое значение, используя старое. Также ярким и простым примером рекурсивных вычислений являются алгоритмы вычисления суммы нескольких чисел и произведения нескольких чисел. Алгоритм накопления счетчика элементов. Еще одна часто встречае- мая задача – подсчет количества элементов последовательности, удовлетво- ряющих заданному условию. Для подсчета количества используют перемен- ную – счетчик, значение которой первоначально равно нулю или, реже едини- це. Далее при выполнении алгоритма в теле цикла значение счетчика увеличи- вается на единицу. Такие счетчики (переменная K) встречались в алгоритмах задач о банковском вкладе вычислении значения функции на интервале. Алгоритм вычисления суммы и произведения нескольких чисел. Алго- ритм вычисления суммы заключается в следующем: сначала переменной, обо- значающей сумму, присваивается значение ноль; далее, в ней будет накапли- ваться значение суммы с прибавлением к старому значению суммы очередного слагаемого при каждом выполнении тела цикла. Алгоритм вычисления произведения аналогичен алгоритму вычисления суммы, с той разницей, что начальному значению произведения присваивается значение единица, а в теле цикла происходит домножение старого значения произведения на очередной сомножитель. В алгоритмах решения задачи о банковских вкладах, в блок-схемах 11 и 12 описанным образом вычисляются счетчик K и сумма вклада X. Задача 11.
Очевидно, что для определения среднего балла по группе нужно вычис- лить среднеарифметическое значение из ряда чисел, состоящего из N элемен- тов, где N – количество человек в группе. Среднеарифметическое значение – это не что иное, как сумма элементов ряда, деленная на их количество. Формализованная постановка задачи выглядит следующим образом:
Исходные данные: N – общее количество студентов Аi – балл i-го студента Выходные данные: SR – средний балл Рабочие переменные: S – общая сумма баллов. Формулы, рассчитывающие результаты: N S = å A i i =1 SR = S/N
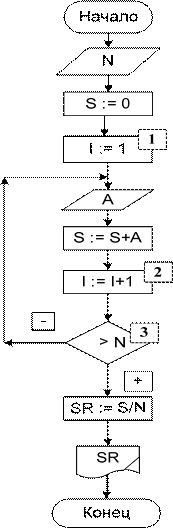
1 Рекурсия – повторение, возвращение. Запишем алгоритм в следующем виде: 1) НАЧАЛО 2) ЦЕЛОЕ N, I 3) ВЕЩЕСТВЕННОЕ A,S, SR 4) ВВОД N; 5) СУММА:= 0; 6) СЧЕТЧИК ЦИКЛА I:= 1; 7) ВВОД ОЧЕРЕДНОГО СЛАГАЕМОГО А; 8) СУММА:= СУММА + А; 9) УВЕЛИЧЕНИЕ СЧЕТЧИКА ЦИКЛА I:= I + 1; 10) ПРОВЕРКА УСЛОВИЯ; 11) ЕСЛИ I < N, ТО ИДТИ НА 5, ИНАЧЕ НА 9; 12) СРЕДНЕЕ:= СУММА / N; 13) ВЫВОД СРЕДНЕЕ; 14) КОНЕЦ. Шаги с 4 по 8 организуют цикл для многократного ввода числа и накоп- ления суммы. Действие 6 можно прокомментировать следующим образом: но- вое значение суммы получается из старого, плюс очередное слагаемое. Алго- ритм решения задачи с использованием цикла с постусловием изображен на блок-схеме 14. Справа от блок-схемы даны пояснения к шагам алгоритма.
ввод количества элементов последова- тельности
блоки подготовки: начальному значе- нию суммы присваивается ноль, счетчику цикла – начальное значение – 1
ввод значения очередного элемента последовательности накопление суммы: к предыдущему значению суммы добавляется очередное сла- гаемое изменение счетчика цикла на единицу проверка условия выхода из цикла: ес- ли очередное значение счетчика цикла пре- высило его конечное значение, то цикл за- канчивается, в противном случае – продол- жается вычисление среднего значения вывод результата
Блок-схема 14 конец алгоритма
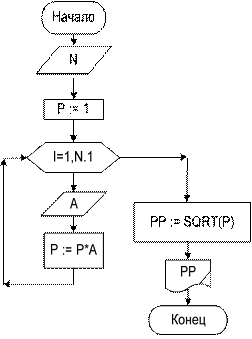
Как и все, рассматриваемые в этом параграфе алгоритмы, описанный ал- горитм можно записать короче, используя блок модификации (блок-схема 15). В блок-схеме 15 три блока схемы 14, помеченных цифрами 1, 2, 3, заменены одним блоком модификации. Запись в блоке модификации означает, что пере- менная I (счетчик цикла) принимает значения от 1 до N с шагом 1, т. е. при пер- вом выполнении цикла – I равно 1, при втором – I равно 2, при третьем – 3, и т. д. до значения N. При I, равной N, тело цикла выполнится последний раз. На блок-схеме 16 изображен алгоритм вычисления среднего геометриче- ского последовательности чисел, состоящий из N элементов. Среднегеометри- ческое – это квадратный корень из произведения элементов ряда.
Задача 12.
Блок-схема 15 Блок-схема 16
Для формализованной постановки задачи необходимо принять некоторые соглашения. Пусть известно, что избирателей будет N человек. Голоса «за» – будем обозначать числом 1, голоса «против» – числом -1, голоса «воздержал- ся» будем обозначать числом 0. Итак, для решения задачи нужно ввести после- довательность из N чисел и определить количество чисел = 1, количество нуле- вых и количество чисел = –1. Исходные данные: N – количество вводимых чисел; A – каждое из вводимых чисел. Выходные данные: KOLРOL – количество положительных чисел; KOLOTR – количество отрицательных; KOLNOL – количество нулевых. Рабочие переменные: i – счетчик цикла совпадает с количеством введен- ных чисел на текущем шаге вычислений; KOLРОL – счетчик положительных голосов; KOLOTR – счетчик отрицательных голосов; KOLNOL – счетчик нулевых чисел. Алгоритм решения задачи представлен на блок-схеме 17.
Блок-схема 17
Комментарии к алгоритму. После блока ввода располагается блок подго- товки, в котором задаются начальные значения количества положительных, от- рицательных и нулевых чисел. Далее идет заголовок цикла в виде блока моди- фикации. Запись в блоке модификации обеспечивает N-кратное выполнение те- ла цикла. В теле цикла вводится очередное значение переменной А, затем с по- мощью ветвления значение A сравнивается с единицей и затем с нулем, и в за- висимости от выполнения условий производятся соответствующие вычисления. Следующим примером использования циклических алгоритмов являются вычисления последовательности чисел, задаваемых рекуррентными соотноше- ниями (формулами). Рекуррентная формула – это соотношение вида: an+p = F(n,an,an+1,...,an+p-1), которое позволяет вычислять все члены последовательности а1,а2, …, если зада- ны ее первые р членов1. В простейшем случае, рекуррентная формула выражает правило вычисления последующего члена последовательности через предыду- щий. Так, член арифметической прогрессии вычисляется по формуле: ai = ai-1 + d, т. е. каждый следующий элемент получается из предыдущего добавлением к нему значения разности.
1 Математическая энциклопедия. – М.: Изд-во Сов. энцикл., 1984. Т. 4 Задача 13.
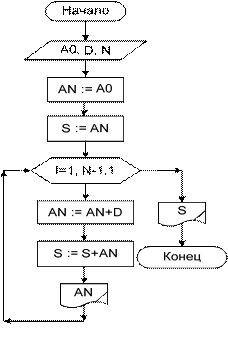
Исходные данные: A0 – первый член прогрессии; D – разность; N – количество членов. Выходные данные: AN – n-й член прогрессии; S – сумма. Рабочие переменные: AN – каждый очередной член прогрессии; I – счетчик цикла совпадает с номером вычисляемого элемента. Известно, что члены арифметической прогрессии задаются рекуррентным соотношением ai = ai-1 + d. Напомним, что рекуррентное соотношение – это формула, выражающая какую-либо величину, зависящую от числа i, через туже величину при меньшем значении i. Для вычислений по рекуррентной формуле такого типа используются рекурсивные вычисления, т. е. это такие вычисления, когда переменная получает новое значение из предыдущего. На блок-схемах 18 и 19 представлены два варианта записи алгоритма решения поставленной зада- чи. Первый вариант – использование цикла с предусловием, второй – использо- вание цикла с параметром.
Алгоритм вычисления очередного элемента прогрессии заключается в том, что (N-1) – кратное выполнение цикла обеспечивает вычисление нового члена прогрессии через предыдущий (текущий). Значения нового и предыдуще- го члена хранятся в одной и той же переменной. На входе у цикла – текущее значение этой переменной. В теле цикла значение этой переменной меняется на новое. При следующем выполнении цикла новое значение уже становится те- кущим. В блоках подготовки задаются начальные значения переменным, которые в теле цикла вычисляются рекурсивно. Это AN – начальный член прогрессии и S – сумма членов. Начальное значение суммы равно не нулю, как это было ре- комендовано в предыдущих примерах, а начальному члену прогрессии, так как его значение нам уже известно. По этой же причине цикл выполняется N-1 раз. Если заданное значение N будет 1, то тело цикла в обоих случаях не выполнит- ся ни разу. Сумма примет значение A0.
Блок-схема 18 Блок-схема 19 Задача 14.
Исходные данные: Переменные для обозначения исходных данных не за- даются. Единственное исходное данное – это количество членов ряда, которое нужно вычислить и напечатать, оно в условии задачи задано константой. Выходные данные: Y – очередное значение числа Фибоначчи. Рабочие переменные: i– счетчик цикла, значение которого совпадает c номером элемента последовательности, Y – очередное (текущее) значение эле- мента последовательности, b – предыдущий элемент последовательности, a – предпредыдущий элемент последовательности. В блок-схеме 20 описан алгоритм решения этой задачи с использованием детерминированного цикла, который будет выполняться 98 раз. Комментарии к алгоритму. После блока «начало» располагаются блоки присваивания и вывода первого (переменная a) и второго (переменная b)числа последовательности. Далее с помощью блока модификации организуется цикл по i от 3 до 100 с шагом 1. Начальное значение счетчика цикла равно трем, так как в теле цикла вычисления начинаются с 3-его элемента ряда. В теле цикла сначала вычисляется и выводится значение очередного (текущего) элемента. Затем рабочие переменные получают новые значения: текущее значение долж- но стать предыдущим, а предыдущее – пред-предыдущим. Поэтому переменная a получает значение b (предыдущего элемента), а переменная b получает значе- ние Y, (текущего элемента). Рядом с блок-схемой 20 показан ход выполнения алгоритма.
1
Y=1+2=3 3 a=2 b=3
Блок-схема 20 i=4
i=5
… Y=2+3=5 5 a=3 b=5
Y=3+5=8 8 a=5 b=8
Из курса математики известно понятие ряда. В данном пособии под поня- тием ряд будем понимать совокупность величин, расположенных в определен- ной последовательности. Существует математическое выражение, зависящее от n, называемое общим членом ряда, определяющее значение n-го члена ряда. Задача 15.
Исходные данные: n – количество элементов ряда; X – параметр ряда. Выходные данные: Y – сумма ряда. Рабочие переменные: i – счетчик цикла совпадает с номером вычисляе- мого слагаемого; S – очередное слагаемое.
Решая эту задачу «в лоб» путем вычисления на каждом i-м шаге частич- ной суммы S:= S + x**i / f, где f – факториал i, получим неэффективный алго- ритм со сложным циклом, требующий выполнения большого числа операций. Гораздо лучше организовать вычисления на основе рекуррентного соотноше- ния между следующим и предыдущим слагаемым. Для этого нужно опреде- лить, каким образом вычисляется очередной член ряда (очередное слагаемое). Подставив несколько значений i в выражение, задающее общий член ря- да, получим следующую картину.
I = 0 S = x^0/0! = 1/1 =1 (факториал 0 равен 1), i = 1 S = x^1/1! = x/1 i = 2 S = x^2/2! = x/1 · x / 2 = x^2 / (1·2) i = 3 S = x^3/3! = x^2 / 2 · x / 3 = x^3 / (2·3) i = 4 S = x^4/4! = x^3 / 6 · x / 4 = x^4 / (6·4) i = 5 S = x^5/5! = x^4 / 24 · x / 5 = x^5 / (24·5) …
. Это соотношение – основа для рекурсивного вычисления очередного сла- гаемого: новое значение слагаемого получается из предыдущего, домножением его на x/i. Алгоритм решения задачи представлен блок-схемой 21 и программой SummaR на АЯРН. Комментарии к алгоритму. В блоке подготовки задаем значение первого слагаемого S (берем его из постановки задачи) и начальное значение суммы Y (оно равно первому слагаемому). Организуем цикл «по i от 1 до n», который будет повторятся n раз, так как в сумму нужно добавить еще n слагаемых. В те- ле цикла сначала вычисляем очередное слагаемое с использованием выведенно- го нами рекуррентного соотношения, затем вычисляем новое значение суммы.
ВЕЩЕСТВЕННОЕ X, S, Y, ВВОД n, X S:= 1 Y:= S
ЦИКЛ по i от 1 до n шаг 1 S:= S*X/i Y:= Y+S
Блок-схема 21 КОНЕЦ ЦИКЛА ВЫВОД Y КОНЕЦ
Программа SummaR1
Не всегда удается вывести рекуррентную зависимость очередного сла- гаемого от предыдущего. В таких случаях вычисление производится «по час- тям». Для этого наиболее часто используются алгоритмы вычисления степени числа и факториала натурального числа. Алгоритмы вычисления степени числа, факториала. Использование операции возведения в степень при работе со степенными рядами приводит к значительному накоплению ошибки результата из-за много- кратного возведения в степень. Если возведение переменной X в любую сте- пень заменить простым умножением, это значительно уменьшит ошибку и со- кратит количество выполняемых исполнителем алгоритма операций. Степень числа – это многократное умножение числа само на себя, т. е. это произведение. Алгоритм вычисления произведения мы уже рассматривали. Та- ким образом, алгоритм вычисления степени – это алгоритм вычисления произ- ведения со следующей модификацией. Начальному значению степени присваи- вается значение 1. Затем, при каждом выполнении цикла новое значение степе- ни получается из старого, домножением его на заданное число. Цикл повторят- ся столько раз, каков показатель степени (блок-схема 22). Факториал натурального числа – это произведение ряда натуральных чи- сел, начиная с 1 и заканчивая заданным числом n! = 1·2·3·…·n (факториал нуля равен 1). Поэтому алгоритм вычисления факториала аналогичен алгоритму вы- числения произведения, с тем отличием, что в качестве сомножителя на каждом выполнении цикла выступает значение счетчика цикла (блок-схема 23).
Обратите внимание, если в том и другом случае будет задано n = 0, то те- ло цикла не выполнится ни разу. Результатом работы алгоритма будет значе- ние 1. В первом случае – любое число в нулевой степени дает 1, и во втором случае факториал нуля – 1. На примере расчета членов степенного ряда рассмотрим алгоритмы вы- числения степеней, факториалов. Учитывая сказанное, для решения задачи 14 можно составить другой алгоритм, добавив в него две дополнительные рабочие переменные: если числитель слагаемого обозначить буквой P (степень числа) и знаменатель буквой F (факториал), то у следующего слагаемого числитель бу- дет равен P и вычисляться рекурсивно: P:= P · X; знаменатель будет равен F и вычисляться рекурсивно: F:= F · i. Само слагаемое вычисляется как S:= P / F. Алгоритм представлен блок-схемой 24 и программой SummaR2 Комментарии к алгоритму. В блоке подготовки задаем значение первого слагаемого S (берем его из постановки задачи) и начальное значение суммы Y (оно равно первому слагаемому). Для вычисления степени и факториала задаем начальные значения переменным P и F соответственно. В теле цикла вычисляем очередное значение степени, очередное значение факториала, очередное сла- гаемое и очередное значение суммы.
НАЧАЛО ЦЕЛОЕ n, i ВЕЩЕСТВЕННОЕ X, S, Y,F, P ВВОД n, X S:= 1 Y:= S F:= 1 P:= 1
ЦИКЛ по i от 1 до n шаг 1 P:= P * X F:= F * i
S:= P/F Y:= Y+S
КОНЕЦ ЦИКЛА ВЫВОД Y КОНЕЦ
Программа SummaR2
Задача 16.
 Вычислить значение R: Вычислить значение R:
Исходные данные: n – количество элементов суммируемого ряда; b – параметр ряда; a0 – начальное последовательности { a }; m – количество элементов второго ряда. Выходные данные: R – искомое значение. Рабочие переменные: i – счетчик цикла совпадает с номером вычисляе- мого слагаемого; SUM – текущее значение суммы; P – текущее значение произведения; a – текущее значение очередного элемента после- довательности { a }; S – очередное слагаемое; ST – степень числа b; F – i! F2 – (i + 1)! S – очередное слагаемое.
Комментарии к постановке задачи. Искомое значение R – это частное от деления суммы на произведение. Сумма состоит из n слагаемых. Каждое слагае- мое суммы представляет собой произведение двух значений. Первый сомножи- тель – степень заданного числа b, зависящая от значения i, где i – номер слагае- мого. Второй сомножитель – очередной член последовательности {a}, каждый из которых определяется по рекуррентной формуле. В записи рекуррентной форму- лы используется факториал числа i, где i – номер слагаемого. Выражение в зна- менателе – это произведение, состоящее из m сомножителей. Каждый сомножи- тель – это частное от деления очередного члена последовательности {a}, на зна- чение факториала от числа (i + 1), где i – номер сомножителя. Указания к составлению алгоритма. Для вычисления искомого значения R нужно сначала определить значение суммы (числителя), затем произведения (знаменателя) для того и другого нужно использовать цикл с известным числом повторений. Следовательно, весь алгоритм решения задачи состоит из двух по- следовательно выполняемых циклов с соответствующими им блоками подго- товки. После завершения второго цикла вычисляется значение R. Комментарии к алгоритму вычисления суммы состоящей из n слагаемых. Цикл с известным числом повторений должен быть организован по счетчику цикла i, где i – номер вычисляемого слагаемого. Каждое слагаемое вычисляется через очередные значения степени числа b, элемента последовательности{ a }, которое в свою очередь вычисляется через очередное значение факториала. По- этому, в теле цикла последовательно вычисляются значения переменных F, ST, a, затем – S, и только после этого значение суммы SUM. Поскольку очередное значение переменных F, ST, a и SUM вычисляется через предыдущее, то перед циклом, в блоке подготовки, должны быть заданы их начальные значения. Ал- горитмы вычисления элементов арифметической последовательности, степени числа и факториала мы уже рассматривали. Для того чтобы понять, с помощью какой последовательности операторов в теле цикла нужно вычислять искомое значение, и что необходимо задать в блоках подготовки цикла, приведем следующий образец рассуждений: вычис- лить нужно сумму, сумму будем вычислять через предыдущее значение (для этого ему нужно задать начальное значение) и новое слагаемое. Новое слагае- мое вычисляем через очередное значение элемента последовательности и сте- пени числа b, поэтому для самого слагаемого не нужно задавать начальные зна- чения. Очередной элемент последовательности вычисляется через факториал. Рассуждения запишем в таблицу (табл. 3). В первой графе записан сформули- рованный вопрос, во второй стрелками показаны направления рассуждений, в третьей графе записываются операторы, которые должны содержаться в теле цикла, в четвертой графе стрелками показана последовательность записи опе- раторов в теле цикла, в пятой графе записаны операции присваивания, которые должны содержаться в блоке подготовки цикла. Таблица 3
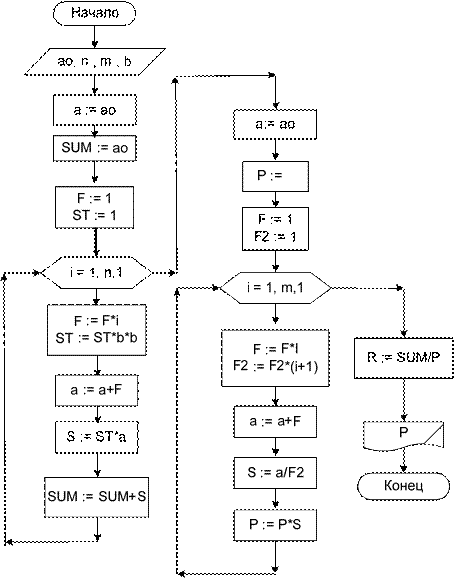
Все эти переменные (F, ST, a) вычисляются рекурсивно (чрез свое преды- дущее значение), поэтому для элемента последовательности, степени и факто- риала нужно задавать начальные значения. При разработке алгоритма все на- чальные значения присваиваем соответствующим переменным в блоке подго- товки цикла. В теле цикла вычислительные блоки записываем, начиная с ниж- них строк таблицы вверх. Для составления алгоритма вычисления произведения проводим анало- гичные рассуждения. Перед циклом задаем начальные значения элемента по- следовательности { a }, произведению и двум факториалам. В теле цикла вычис- ляем сначала оба факториала, очередной элемент последовательности { a }, за- тем очередное слагаемое и, наконец, очередное значение произведения. Весь алгоритм решения поставной задачи описан в блок-схеме 25.
Блок-схема 25
Итерационные циклы Циклы, в которых число повторений неизвестно из исходных данных и не может быть определено заранее в процессе исполнения алгоритма, называют итерационными. В итерационном цикле на каждом шаге вычислений (т. е. при каждом выполнении тела цикла) происходит: – во-первых, последовательное приближение к значению результата, – во-вторых, проверка условия, в котором задается либо конечный ре- зультат, либо точность (погрешность) вычислений. Такие шаги называются итерациями. Выход из итерационного цикла осуществляется в случае выполнения заданного условия, т. е. выполнение ите- раций прекращается, если найден конечный результат, либо заданная точность вычислений. В итерационных циклах для организации выхода из тела цикла преду- сматривается проверка некоторого заранее заданного условия, для чего исполь- зуют блок проверки условия. В итерационных циклах невозможно использо- вать блоки модификации, так как при организации таких циклов заранее неиз- вестно количество изменений переменной цикла и ее конечное значение. Итерационные циклы мы уже использовали в алгоритме Евклида и в алго- ритме решения задач 7 и 8 о банковском вкладе. Рассмотрим еще несколько задач. Задача 17.
Исходные данные: N пог. м/день – производительность первой ткачихи; M пог. м/день – производительность второй ткачихи. Выходные данные: T – количество дней; S – суммарное количество ткани. Рабочие переменные: K – общее количество ткани, изготовленное первой ткачихой; P – общее количество ткани, изготовленное второй ткачихой. Алгоритм решения задачи – в блок-схеме 26. Комментарии к алгоритму. После блока ввода исходных данных осуще- ствляется их проверка, так как по условию задачи M должно быть больше N. Если M не больше N, то выполняется перестановка из значений с помощью ра- бочей переменной R. Эта переменная используется здесь для временного хра- нения значения переменной N. Основной алгоритм должен быть реализован с помощью итерационного цикла: цикл должен выполняться пока количество ткани, изготовленное второй ткачихой, меньше количества ткани, изготовлен- ного первой ткачихой.
Алгоритм перестановки зна- чений двух переменных.
Номер дня, когда начала ра- ботать вторая ткачиха. К концу это- го дня первая ткачиха проработала 2 дня и изготовила K пог. м ткани, вторая ткачиха проработала 1 день и изготовила P пог. м ткани.
Пока P<K, выполняется тело цикла.
В цикле считается: количест- во дней, количество ткани, изготов- ленное первой и второй ткачихой.
Блок-схема 26 Задача 18.
Исходные данные: N деталей/мес. – производительность станка; M лет – гарантийный срок; P – деталей/мес. – минимально допустимая произ- водительность станка; K – деталей/мес. – падение производительности станка после гарантийного срока. Выходные данные: L – количество лет, которое проработает станок; KOL – суммарное количество деталей. Рабочие переменные: T – счетчик месяцев, которые проработает станок после истечения гарантийного срока; N – текущая производительность станка; KOL – счетчик количества деталей. Алгоритм решения задачи – в блок-схеме 27 и программе «Станок».
ЦЕЛОЕ M, N, K, P, KOL, L, N
KOL:= 12*M*N ! количество деталей изготовленных станком в течение гарантийного срока! T:= 1
N:= N – K KOL:= KOL + N T:= T+1
КОНЕЦ ЦИКЛА
L:= M+T/12 ВЫВОД L, KOL КОНЕЦ Программа Станок
Для вычисления приближенных значений многих математических функ- ций используются разложение их в степенные ряды. Ряды могут быть конеч- ными, тогда для их вычисления используются циклы с известным числом по- вторений, и бесконечными, что приводит к необходимости использования ите- рационных циклов. При разложении функции в степенной ряд задается точ- ность вычислений ее приближенного значения. Таким образом, цикл повторя- ется до тех пор, пока не будет достигнута заданная точность вычислений. Задача 19.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 1305; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.173.227 (0.252 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
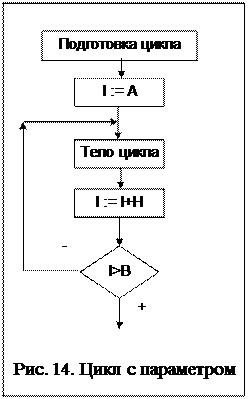 Для записи циклов с известным числом повторений часто используется управляющая структура «Цикл-до» (рис. 14), в которой зада- ются параметры цикла: i – счетчик цикла, А – начальное значение счетчика цикла, В – конеч- ное значение счетчика цикла, H – шаг измене- ния счетчика цикла.
Для записи циклов с известным числом повторений часто используется управляющая структура «Цикл-до» (рис. 14), в которой зада- ются параметры цикла: i – счетчик цикла, А – начальное значение счетчика цикла, В – конеч- ное значение счетчика цикла, H – шаг измене- ния счетчика цикла.
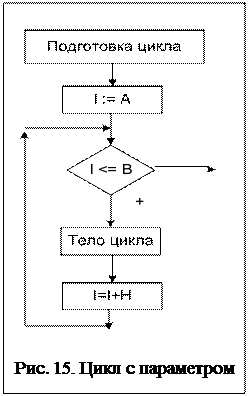
 Как видно из рис. 14 и 15 в качестве пе- ременной цикла используется счетчик цикла, значение которого меняется по определенной закономерности. Счетчик цикла используется для подготовки очередного повторения цикла и отслеживания условий его окончания. В качест- ве счетчика цикла используют любые перемен- ные, индексы массивов, аргументы вычисляе- мых функций и тому подобные величины. Во время выполнения тела цикла счетчик цикла изменяется в интервале от начального до ко- нечного значения с заданным шагом. Следова- тельно, при организации циклов с параметром необходимо предусмотреть задание начального значения счетчика цикла, закон его изменения перед каждым новым повторением и его конеч- ное значение, при достижении которого про- изойдет завершение цикла.
Как видно из рис. 14 и 15 в качестве пе- ременной цикла используется счетчик цикла, значение которого меняется по определенной закономерности. Счетчик цикла используется для подготовки очередного повторения цикла и отслеживания условий его окончания. В качест- ве счетчика цикла используют любые перемен- ные, индексы массивов, аргументы вычисляе- мых функций и тому подобные величины. Во время выполнения тела цикла счетчик цикла изменяется в интервале от начального до ко- нечного значения с заданным шагом. Следова- тельно, при организации циклов с параметром необходимо предусмотреть задание начального значения счетчика цикла, закон его изменения перед каждым новым повторением и его конеч- ное значение, при достижении которого про- изойдет завершение цикла.
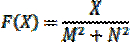 Вычислить значение функции
Вычислить значение функции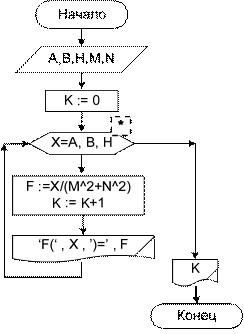
 Блок-схема 13 Блок-схема 12
Блок-схема 13 Блок-схема 12 Группа студентов сдавала тесты. Известно общее количество человек и баллы, набранные каждым студентом. Определить средний балл по группе.
Группа студентов сдавала тесты. Известно общее количество человек и баллы, набранные каждым студентом. Определить средний балл по группе.
 Начало алгоритма
Начало алгоритма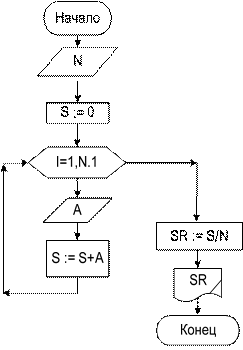
 На предприятии проводятся выборы предложенной кандидатуры пред- седателя профкома. В урну опускаются бюллетени, на которых избира- тели должны проголосовать «за», «против» или «воздержался». Необхо- димо подсчитать количество голосов «за», «против» и «воздержался».
На предприятии проводятся выборы предложенной кандидатуры пред- седателя профкома. В урну опускаются бюллетени, на которых избира- тели должны проголосовать «за», «против» или «воздержался». Необхо- димо подсчитать количество голосов «за», «против» и «воздержался».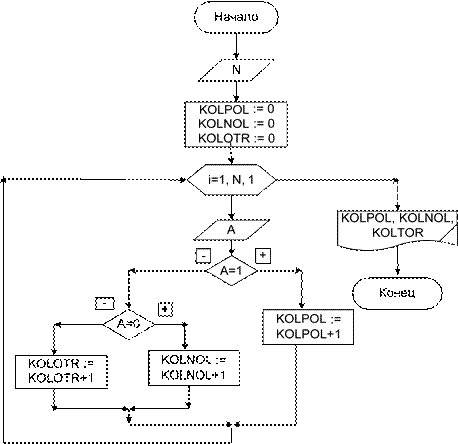

 Вычислить и напечатать n членов арифметической прогрессии и их сум- му.
Вычислить и напечатать n членов арифметической прогрессии и их сум- му.
 Напечатать последовательность ста чисел, составляющих ряд Фибонач- чи. Каждое число ряда Фибоначчи вычисляется как сумма двух преды- дущих, например: 1, 2, 3, 5, 8, 13, 21 ….
Напечатать последовательность ста чисел, составляющих ряд Фибонач- чи. Каждое число ряда Фибоначчи вычисляется как сумма двух преды- дущих, например: 1, 2, 3, 5, 8, 13, 21 ….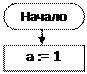 a=1; b=2;
a=1; b=2;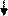 2
2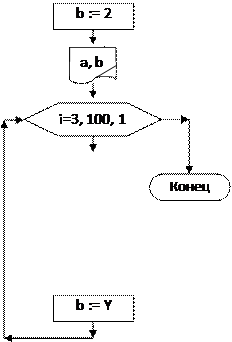 i=3
i=3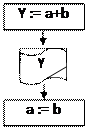
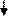
 Вычислить сумму конечного степенного ряда:
Вычислить сумму конечного степенного ряда: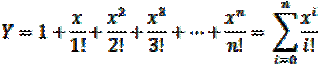
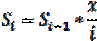 Становится ясно, что каждое новое слагаемое получается из предыдущего домножением его на дробь x на i. Запишем рекуррентную формулу
Становится ясно, что каждое новое слагаемое получается из предыдущего домножением его на дробь x на i. Запишем рекуррентную формулу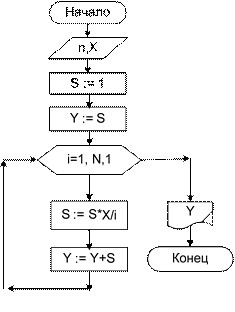 НАЧАЛО ЦЕЛОЕ n, i
НАЧАЛО ЦЕЛОЕ n, i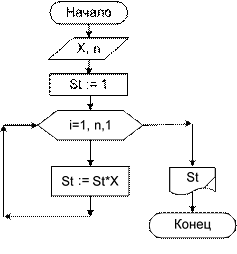
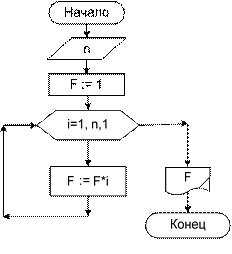
 Блок-схема 22 Блок-схема 23
Блок-схема 22 Блок-схема 23

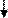 Блок-схема 24
Блок-схема 24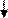
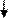
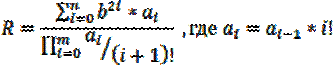
 Одна ткачиха в течение рабочего дня изготавливает N погонных метров ткани, а вторая – M погонных метров (M > N). Обе ткачихи начали рабо- ту на однотипных станках, но вторая – на один день позже. Через сколь- ко дней вторая ткачиха догонит первую, и какое количество ткани они изготовят за это время?
Одна ткачиха в течение рабочего дня изготавливает N погонных метров ткани, а вторая – M погонных метров (M > N). Обе ткачихи начали рабо- ту на однотипных станках, но вторая – на один день позже. Через сколь- ко дней вторая ткачиха догонит первую, и какое количество ткани они изготовят за это время?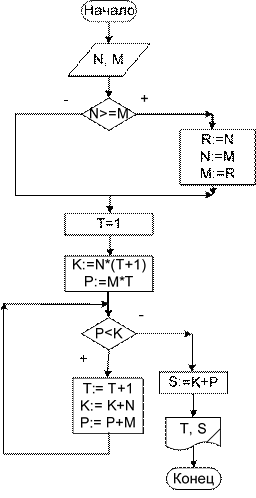 Ввод исходных данных
Ввод исходных данных Станок по изготовлению деталей в течение гарантийного срока (M лет) имеет производительность N изделий в месяц. После истечения гаран- тийного срока его производительность падает на K изделий в месяц. Сколько полных лет проработает станок до тех пор, пока его производи- тельность не упадет до минимально допустимого значения (P) и сколько изделий он за это время изготовит.
Станок по изготовлению деталей в течение гарантийного срока (M лет) имеет производительность N изделий в месяц. После истечения гаран- тийного срока его производительность падает на K изделий в месяц. Сколько полных лет проработает станок до тех пор, пока его производи- тельность не упадет до минимально допустимого значения (P) и сколько изделий он за это время изготовит.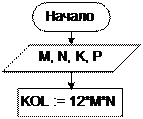 НАЧАЛО
НАЧАЛО ВВОД M,N,K,P
ВВОД M,N,K,P
 Блок-схема 27
Блок-схема 27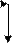 ПОКА N>P ПОВТОРЯТЬ:
ПОКА N>P ПОВТОРЯТЬ: ! пока производительность больше ми- нимально допустимой!
! пока производительность больше ми- нимально допустимой!