Основные законы движения кулачковых механизмов

Кулачковые механизмы могут проектироваться с любым произвольным законом движения ведомого звена. С целью унификации детально разработаны и рекомендованы к применению следующие основные законы. Каждый основной закон получил буквенный шифр.

 

1). «А» - Закон постоянной скорости (V = const)

График ускорения - а,м/с²; скорости – V,м/с и пути - S,м для этого закона показаны на рис.15-а. Поскольку скорость постоянна, график пути по времени представляет собой наклонную прямую, а ускорение равно нулю. Од­нако в начале и конце движения скорость резко меняет свое значе­ние. В эти моменты возникает бесконечное по величине ускорение и механизм будет испытывать жесткий динамический удар. Поэтому этот закон применяется только в комбинации с другими законами движения. Расчетными формулами для а того закона являются:

           S = V × t; V = S₀ / T; a = ± ¥           (6.4)

Здесь Т – период движения толкателя (рабочий или холостой ход), с;

        t – любой, задаваемый в пределах Т, момент времени, с.

 

2). «П» - Закон постоянного ускорения (а = const).

Графики этого закона даны на рис.15-б. В первой половина движения (разгон) при 0 < t< Т/2 ускорение положительно, во второй половине (торможение) при Т/2 < t < Т ускорение отрицательно. В начале, середине и конце движения уско­рение резко меняет свое значение от нуля до + a_max, от + a_max до – a_max и от – a_max до нуля. Поэтому в механизме в эти мо­менты возникают мягкие удары.

Скорость в первой половине движения равномерно возрастает, во второй половине – убывает. Расчет графиков пути, скорости и ускорения ведется по формулам:

а) для периода разгона при 0 < t< T/2

S = 2S₀ (t / T)²;

V = 4 S₀ /T (t / T);

                             a = 4S₀ / T².                         (6.5)

Построив по формулам (6.5) график пути, строим профиль кулачка.

3). «К» - Закон косинусоидального изменения ускорения (a = f (cos)).

Графики этого закона приведены на рис. 15-в. В первой половине движения (разгон) при 0 < t < T/2 ускорение положительно, во второй (торможение) при Т/2 < t< Т) – отрицательно. В начале движения ускоре­ние резко возрастает до + a_max, в конце движения оно резко изменяется от

- a_max до нуля. Поэтому в начале и конце движения возникнут мягкие удары. В середине движения, в отличие от предыдущего закона, ускорение меняет свое значение плавно и удара не будет.

Расчет графиков пути, скорости и ускорения проводится по формулам:                S = S₀/2 (1 – cos p t/T);

                           V = p/2 × S₀/T × sin p t/T; V_max = pS₀/2T;   (6.6)

            a = p²/2 × S₀/T × cos p t/T; a_max = ± 4,93 S₀/T²

 

 

Рис.15. Основные законы движения толкателя кулачковых

механизмов

4). «С» - Закон синусоидального изменения ускорения (а = f (sin)).

Графики этого закона показаны на рис.15-г. При этом законе ускорение плавно меняет свою величину, и механизм работает без ударов. Расчет графиков пути, скорости и ускорения ведется по формулам:

S = S₀/2 (2p t/T – sin 2p t/T);

                                V = S₀ (1 – cos 2p t/T); V_max = 2 S₀/T;        (6.7)

               a = 2p S₀/T sin 2p t/T; a_max = 6,28 S₀/T²            

Сравнивая эти законы, следует обратить внимание на конечные величины максимальных ускорений:

«П» - закон постоянного ускорения:                   а = 4 S₀/T²;

«К» - закон косинусоидального ускорения:       a_max = 4,93 S₀/T²;

«С» - закон синусоидального ускорения:           a_max = 6,28 S₀/T².

Первый закон – «П» наиболее простой, дает наименьшее ускорение. Однако кулачек работает с ударами. Поэтому этот закон следует принимать для тихоходных малонагруженных механизмов.

Последний синусоидальный закон - «С» удобен тем, что механизм работает без ударов, однако максимальное ускорение – а_max у него наиболее высокое, следовательно и силы инерции в механизме будут наибольшими. Поэтому часто прибегают к использованию косинусоидального закона – «К».

Значение ускорений в механизме необходимо для технологических расчетов машины (например, при слишком большом ускорении жидкость может выплеснуться из сосуда) и для конструктивных расчетов, поскольку знание сил инерции, возникающих в механизме, дает возможность рассчитать силовое замыкание механизма (см. ХХ гл. учебника [1]) и провести расчет на прочность звеньев механизма.

Проектируя кулачковый механизм, конструктор может по своему желанию принять закон движения и выбрать коэффициент срабатывания.

В машинах-автоматах кроме кулачковых применяется много жесткозвенных базисных механизмов, которым присущи свои общие и специфические кинематические зависимости. Они произвольно выбираться не могут.

Ознакомимся с некоторыми из этих механизмов.

Кривошипно-ползунный механизм

   

 Кривошипно-ползунные механизмы имеют две модификации:

1) дезаксиальные механизмы, у которых центр вращения кривошипа. смещен относительно оси движения ползуна на некоторое расстояние - е («дезаксиал»);

 2) аксиальные механизмы, у которых ось вращения кри­вошипа находится на оси движения ползуна и е =0, (рис.16).

При вращении кривошипа ОА ползун В получает возвратно-поступательное движение, проходя максимальный путь - S_max. Крайние положения ползуна В₀ и В₂ соответствуют положениям кривошипа ОА₀ и ОА₂, при которых геометрические оси кривошипа и шатуна АВ совпадают.

В силовых механизмах отношение радиуса кривошипа-R к длине шатуна - l принимается около 1/50;

 

Рис.16. Схема кривошипно-ползунного механизма

Если задана частота вращения кривошипа в минуту- n, то его

угловая скорость, как известно, составит w, рад/с:

w = pn/30,

а кинематический цикл по формуле (2.1) равен, с: Т_к = 60/n.

Вспомнив, что вообще w = j/t, найдем время рабочего и холос­того ходов ползуна: t_p = j_p/w: t_x = j_x/w;

где j_p и j_x – углы поворота кривошипа, соответствующие рабочему

и холостому ходам. В частном случае для аксиаль­ного механизма они равны между собой, для дезаксиального механизма они замеряются по схеме, построенной в масштабе.

Выразив угловую скорость кривошипа - w,с^-1 через частоту его вращения - n,об/мин получим:

                         t_p = 30 j_p/pn;  t_x = 30 j_x/pn            (6.8)

 

Найдем теперь коэффициент срабатывания механизма

                                    К = t_x/t_p = j_x/j_p                                       (6.9).

Таким образом, коэффициент срабатывания кривошипно-шатунного механизма зависит от размеров его звеньев и не может при составле­нии циклограммы выбираться произвольно.

Продолжительность рабочего и холостого ходов ползуна можно выразить через коэффициент срабатывания и кинематический цикл. Действительно, кинематический цикл механизма – Т_к,с равен сумме времен t_p и t_x

                             T_к = t_p + t_x                                                           (6.10)

Из формулы (6.9) следует, что t_x = к × t_p. Подставив это значение t_x в последнюю формулу (6.10), получим

Т_к = t_p + к × t_p = t_p (к + 1).

Отсюда                              t_p = T_к /(к + 1)                             (6.11)

 

а так как t_x = к × t_p, то t_x = T_к × к / (к +1)                                   (6.12)

В аксиальном механизме углы рабочего и холостого хо­дов равны между собой: j_р = j_х = p = 180⁰.

Из формулы (6.9) следует, что К = 1, а из формулы (6.11) и (6.12) следует, что                   

                                   t_p = t_x = T_к/2 = 30/n                          (6.13)

 

Таким образом, как время рабочего хода, так и время холостого хода равны половине кинематического цикла, и при составлении циклограммыих можно принимать одинаковыми.

Разберем основные кинематические и динамические закономерности аксиального кривошипно-ползунного механизма.

Если кривошип ОА радиусом R повернетсяиз исходного положения ОА на угол j и займет некоторое положение ОА, то ползун пройдет путь S, равный отрезку А₀С, величину которого можно выразить, как

S = A₀C = OA₀ – OC

или                         S = R – R × cos j = R (1 – cos j)                 (6.14)

 

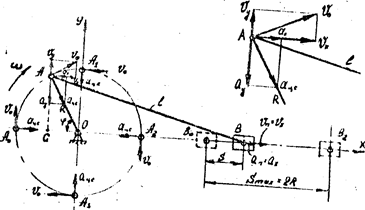
На схеме (рис.16) принято, что кривошип вращается по часо­вой стрелке с угловой скоростью - w,с^-1. Окружная скорость шарнира А кривошипа – V₀,м/с всегда направлена по касательной к окружности, описываемой точкой А в сторону вращения, и равна V₀ = w × R. При вращении кривошипа из положения А₀ вположение А₂ ползун движет­ся вправо, а при вращении из положенияА₂ в положение А₀ – влево. Если вектор окружной скорости –V₀ разложить на две составляющие:

горизонтальную V_x = V₀ × sin j и вертикальную V_y = V₀ × cos j, то легко увидеть, что скорость ползуна-V_n равна горизонтальной составляющей

                 V_n = V₀ × sin j; или  V_n = w × R × sin wt              (6.15)

 

Другими словами, скорость ползуна равна проекцииокружнойскорости кривошипа на ось движения ползуна.

В положении кривошипа А₁ (j = 90⁰) ползунимеет максимальную положительную скорость V_n = w R (векторокружной скоростикривошипа параллелен оси движения ползунаи полностью проецируется на ось движения кривошипа), в положениикривошипа А₃ ( j = 270⁰ ) скорость ползуна будет такжемаксимальна, но отрицательна: V_n = - w R (вектор окружной скорости также полностью проецируется на ось движения ползуна).

В положениях кривошипа А₀ и А₂ (j₀ = 0 и j₂ = 180⁰) ползун не имеет направлений движения, и скорость его равна нулю (векторы окружной скорости V₀, перпендикулярны оси движения ползуна и при проецировании на нее обращаются в ноль).

Поскольку кривошип вращается с постоянной скоростью, тоегошарнир А будет обладатьтолько нормальным (центростремительным) ускорением – а_цс = w² R, вектор которого всегда, независимо от направлений вращения, направлен по радиусу к центру вращения.

Если вектор центростремительного ускорения а_цс разложить на два составляющих: горизонтальный - а_х и вертикальный - а_у,то легко увидеть, что ускорение ползуна а _n равно горизонтальной составляющей ценростремительного ускорения а _х, т. е.

             a_n = w² × R × cos j; или a_n = w² × R × cos wt                   (6.16)

 

В положении кривошипа А₀ (j₀ = 0) ускорение ползуна максимально и равно центростремительному ускорению: а_n = w² × R (вектор центростремительного ускорения полностью проецируется на ось движения ползуна); в положении кривошипа А₂ (j₂ = 180⁰) ускорение ползуна также максимально, но обратно по знаку: a_n = - w² × R.

В промежуточных положениях А₁ (j₁ = 90⁰) и А₃ (j₃ = 270⁰) ускорение ползуна равно нулю, поскольку векторы центростремительного ускорения перпендикулярны к оси движения ползуна и при проецировании на нее обращаются в ноль.

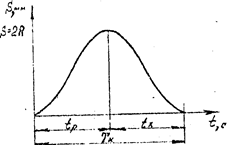
Таким образом, скорость ползуна изменяется по синусоидальному закону, а ускорение – по косинусоидальному закону. Согласно формуле (6.12) путь, пройденный ползуном, изменяется по косинусоидальному закону и поэтому синхрограмма движения ползуна представляет собой косинусоиду (рис.17).

Рис.17. Синхрограмма ползуна кривошипно-ползунного механизма

Поскольку ползун движется неравномерно, с ускорением, постольку он, в соответствии со вторым законом Ньютона, будет обладать силой инерции - Р, Н.

                 Р = - m × a_n                                            (6.17)

где m – масса ползуна, кг.

Знак минус говорит о том, что сила инерции всегда направлена в сторону, противоположную направлению ускорения. Следует об­ратить внимание на то, что если направление скорости ползуна зависит от направления вращения кривошипа, то направление ускорения ползуна от направления вращения кривошипа не зависит, поскольку направление центростремительного ускорения не зависит от направления вращения кривошипа.

Направления ускорения - a_n исилы инерции – Р ползуназависят только от угла поворота и положения кривошипа:

I-й квадрант (j = 0 - 90°)       a_n – положительно, Р – отрицательно; 

II-й квадрант (j = 90 - 180°) a_n – отрицательно, Р – положительно;     

III-й квадрант (j = 180^о - 270°) a_n – отрицательно, Р – положительно;       IУ-й квадрант (j = 270^о –360^о ) a_n – положительно, Р – отрицательно;

Следовательно, для того чтобы найти направление силы инерции, необходимо вначале определить направление ускорения.

  

Четырехзвенный рычажно-шарнирный механизм

Механизм (рис.18.) состоит из ведущего звена – кривошипа О₁А длиной r₁, соединительного звена – шатуна АВ длиной l₂, ведомого звена – коромысла О₂В длиной R₃ и неподвижного звена – основания О₁О₂ длиной l₄.

                  

 

           Рис. 18. Схема четырехзвенного механизма.

При вращении кривошипа коромысло О₂В совершает качательное движение без выстоев на угол y, а его точка В описывает дугу В¢В¢¢. Этим механизмом можно осуществить и возвратно-поступательное движение ползуна Д, если соединить его тягой СД, например, с точкой С коромысла.

Такой механизм может существовать лишь при определенном соотношении размеров его звеньев. По теореме Грасгофа четырехзвенный механизм возможен, если сумма наибольшего и наименьшего звеньев будет не больше суммы двух остальных, т.е.

r₁ + l₄  £ R₃ + l₂                                   (6.18.)

Зависимость угла качания коромысла y от угла поворота кривошипа j выражается формулой

                                          _________

y =arcsin[r₁ · a ± b √ 4r₃² d²  - a²  / (2r₃ d² )]                    (6.19)

                                                                                     

где: a = d² – (l₂ ² – r₃²) · sin φ;

b = l₄ – r₁ · cos φ;

             d² = r₁² – 2r₁l₄ cos j + l₄²

Эта формула для ручного расчета достаточно громоздка, поэтому практически либо ограничиваются графическим построением как угла y, так и промежуточных положений коромысла, либо делают расчет на ЭВМ по заранее составленной программе.

При необходимости регулирования угла качания коромысла механизм конструируют либо с регулируемым радиусом r₁ кривошипа О₁А, либо с шарниром В, перемещаемым вдоль коромысла. В последнем случае меняется R₃. Чем больше r₁, тем больше угол качания y и наоборот, чем больше R₃, тем меньше угол y.

 

Кулисный механизм

 

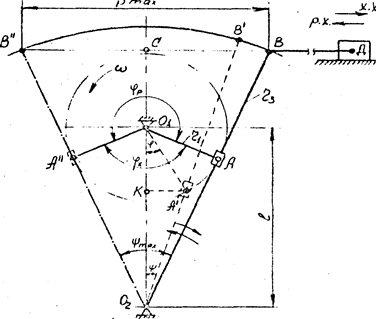
Кулисный механизм (рис.19) состоит из ведущего звена - вращающегося кривошипа О₁А радиусом r₁, связанного шарнирно с ползуном А, который может свободно скользить по ведомому звену – кулисе О₂В. При вращении кривошипа ползун, скользя по кулисе, заставляет ее совершать качательное движение на угол y. В крайних положениях кулиса располагается по касательной к окружности, описываемой точкой А, поэтому угол О₁АО₂ прямой, а угол холостого хода j_х будет всегда меньше угла рабочего хода j_р.

При помощи этого механизма можно получить возвратно-поступательное движение ползуна Д, если его соединить тягой с точкой В кулисы. Такой механизм применяется, например, для привода суппорта в поперечно-строгальном станке.

 

Рис. 19. Схема кулисного механизма.

 

                  Рассмотрим основные конструктивные и кинематические зависимости кулисного механизма. Одним из основных конструктивных параметров механизма является отношение межцентрового расстояния - l к радиусу кривошипа - r₁.

                                    l = l / r₁                                                           

  Из треугольника О₁АО₂ следует, что

                  l / r₁ = 1/ sin(y/2) = l,                                     (6.16)

а из треугольника О₂ВС следует, что

sin(y/2) = CB/O₂B = S_max/2 r₃.

Следовательно:

l = 2 r₃ / S_max; и S_max = 2 r₃ / l = 2 r₁ r₃ / l                     (6.17)

Из последней формулы видно, что путь ползуна S_max тем больше, чем больше радиус кривошипа r₁ или длина кулисы r₃ и тем меньше, чем больше межцентровое расстояние l. Для возможности изменения хода ползуна обычно механизм проектируют с регулируемой длиной кривошипа r₁. Задаваясь двумя конструктивными параметрами, по этой формуле можно определить третий.

Зная l, можно рассчитать углы рабочего j_р и холостого j_х ходов механизма: из треугольника О₁АО₂ следует, что cos(j_х/2) = r₁ / l = 1 /l, cледовательно:

j_х = 2 arccos(1/l) и j_p = 2 (p - arccos(1/l))                    (6.18)

Как и в кривошипно-ползунном механизме время холостого хода – t_x и рабочего хода - t_p будут пропорциональны соответствующим уг­лам j_х и j_р:

t_x = j_x / w = 30 j_x / (p n)   t_p = j_p / w = 30 j_p / (p n)

Следовательно, коэффициент срабатывания механизма будет также равен отношению этих углов

                     K = t_x / t_p = j_x / j_p

Практически в этих механизмах К = 0.6 – 0.8. Поскольку

  j_р + j_х = 2 p, а j_х = К × j_р , то

  j_р + К × j_р  = 2p   и  j_р (1 + К) = 2 p.

Отсюда найдем угол рабочего хода, выраженный через коэффициент срабатывания:

j_р  = 2 p / (К + 1), а также угол холостого хода j_х = 2 p К / (К + 1). (6.19)

Найдем зависимость угла качания кулисы - y_max от коэффициента срабатывания. Из треугольника О₁ АО₂ следует, что:

y_max / 2 = p / 2 - j_x /2, или y_max  = p - j_x.

Подставив сюда значения j_х из (6.19), получим:

                       y_max  = p (1 – K) / (1 + K),                        (6.20)          Для определения закона изменения угловой скорости коромысла и его углового ускорения рассмотрим механизм с промежуточным положением коромысла О₂В и будем отсчитывать углы от средней оси механизма: положение кривошипа определится углом j, коромысла – углом y.

Очевидно, что tg y = A¢K / KO₂ = r₁ sin j / (l – r₁ cos j) = sin j / (l - cos j),              И тогда y = arctg (sin j / (l - cos j))                       (6.21)

Угловая скорость  w₃ = dy / dt, т.е. в нашем случае угловая ско­рость холостого хода кулисы - w_3x, c ^–1 будет:

w_3x = dy / dt = (d/dt) · arctg(sin j / (l - cos j)) =

= - ω₁ (l cos j - 1)/(l² - 2λcos j + 1).                 (6.22)   

              Здесь ω₁ = dφ/dt – угловая скорость кривошипа, а знак минус показывает, что w_3x противоположна ω₁ .

Угловая скорость холостого хода будет максимальна при φ = 0

(среднее положение кулисы).

                                    [w_3x ]_max = ω₁ /(λ – 1).                          (6.23)

Для рабочего хода коромысла аналогичным образом можно получить:

w_3x = ω₁ (l cos j - 1) / (l² - 2λcos j + 1).               (6.22)

Поскольку эта скоросгь будет максимальна также в среднем положении (при φ = π), то:

                       [w_3x ]_max = ω₁ /(λ + 1).                           (6.23)

Точка В кулисы будет обладать максимальной линейной скоростью в среднем положении кулисы при ее холостом ходе:

[v_вх ]_max = [w_3x ]_max · r₃ = - ω₁· r₃ /(λ – 1).                    (6.24)

Для получения закона изменения углового ускорения - ε₃ , рад/с² во время рабочего хода кулисы продифференцируем уравнение(6.22):

ε_3р = dω_3p /dt = ω₁² λ (λ² – 1) · sin φ / (l² - 2λcos j + 1)² .   (6.25)

Таким образом, по конструктивному параметру λ = L / r₁, пользуясь формулой (6.21), можно рассчитать угловое перемещение – ψ кулисы и построить синхрограмму. Тот же параметр позволяет определить угловые скорости – ω₃ и ускорения – ε₃ кулисы при любой угловой скорости кривошипа в любом его положении, определяемым углом поворота – φ.