
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Магнитные моменты электронов и атомов
Рассматривая действие магнитного поля на проводники с током и на движущиеся заряды, мы не интересовались процессами, происходящими в веществе. Свойства среды учитывались формально с помощью магнитной проницаемости m. Для того чтобы разобраться в магнитных свойствах сред и их влиянии на магнитную индукцию, необходимо рассмотреть действие магнитного поля на атомы и молекулы вещества. Опыт показывает, что все вещества, помещенные в магнитное поле, намагничиваются. Рассмотрим причину этого явления с точки зрения строения атомов и молекул, положив в основу гипотезу Ампера, согласно которой в любом теле существуют микроскопические токи, обусловленные движением электронов в атомах и молекулах. Для качественного объяснения магнитных явлений с достаточным приближением можно считать, что электрон движется в атоме по круговым орбитам. Электрон, движущийся по одной из таких орбит, эквивалентен круговому току, поэтому он обладает орбитальным магнитным моментом (см. (109.2)) pm=ISn, модуль которого
где I=en — сила тока, n — частота вращения электрона по орбите, S — площадь орбиты. Если электрон движется по часовой стрелке (рис. 187), то ток направлен против часовой стрелки и вектор рm (в соответствии с правилом правого винта) направлен перпендикулярно плоскости орбиты электрона, как указано на рисунке. С другой стороны, движущийся по орбите электрон обладает механическим моментом импульса Le, модуль которого, согласно (19.1),
где v = 2pn, pr2 = S. Вектор Le (его направление также определяется по правилу правого винта) называется орбитальным механическим моментом электрона. Из рис. 187 следует, что направления рm и Le, противоположны, поэтому, учитывая выражения (131.1) и (131.2), получим
где величина
называется гиромагнитным отношением орбитальных моментов (общепринято писать со знаком «–», указывающим на то, что направления моментов противоположны). Это отношение, определяемое универсальными постоянными, одинаково для любой орбиты, хотя для разных орбит значения v и r различны. Формула (131.4) выведена для круговой орбиты, но она справедлива и для эллиптических орбит. Экспериментальное определение гиромагнитного отношения проведено в опытах Эйнштейна и де Гааза* (1915), которые наблюдали поворот свободно подвешенного на тончайшей кварцевой нити железного стержня при его намагничении во внешнем магнитном поле (по обмотке соленоида пропускался переменный ток с частотой, равной частоте крутильных колебаний стержня). При исследовании вынужденных крутильных колебаний стержня определялось гиромагнитное отношение, которое оказалось равным –(e/m). Таким образом, знак носителей, обусловливающих молекулярные токи, совпадал со знаком заряда электрона, а гиромагнитное отношение оказалось в два раза бо2льшим, чем введенная ранее величина g (см. (131.4)). Для объяснения этого результата, имевшего большое значение для дальнейшего развития физики, было предположено, а впоследствии доказано, что кроме орбитальных моментов (см. (131.1) и (131.2)) электрон обладает собственным механическим моментом импульса Les, называемым спином. Считалось, что спин обусловлен вращением электрона вокруг своей оси, что привело к целому ряду противоречий. В настоящее время установлено, что спин является неотъемлемым свойством электрона, подобно его заряду и массе. Спину электрона Les, соответствует собственный (сотовый) магнитный момент рms, пропорциональный Les и направленный в противоположную сторону:
*В. И. де Гааз (1878—1960) — нидерландский физик.
Величина gs называется гиромагнитным отношением спиновых моментов. Проекция собственного магнитного момента на направление вектора В может принимать только одно из следующих двух значений:
где ħ=h/(2p) (h—постоянная Планка), mb—магнетон Бора, являющийся единицей магнитного момента электрона.
В общем случае магнитный момент электрона складывается из орбитального и спинового магнитных моментов. Магнитный момент атома, следовательно, складывается из магнитных моментов входящих в его состав электронов и магнитного момента ядра (обусловлен магнитными моментами входящих в ядро протонов и нейтронов). Однако магнитные моменты ядер в тысячи раз меньше магнитных моментов электронов, поэтому ими пренебрегают. Таким образом, общий магнитный момент атома (молекулы) pa равен векторной сумме магнитных моментов (орбитальных и спиновых) входящих в атом (молекулу) электронов:
Еще раз обратим внимание на то, что при рассмотрении магнитных моментов электронов и атомов мы пользовались классической теорией, не учитывая ограничений, накладываемых на движение электронов законами квантовой механики. Однако это не противоречит полученным результатам, так как для дальнейшего объяснения намагничивания веществ существенно лишь то, что атомы обладают магнитными моментами. 37. Колеба́ния — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия. Колебания почти всегда связаны с попеременным превращением энергии одной формы проявления в другую форму. Колебания различной физической природы имеют много общих закономерностей и тесно взаимосвязаны c волнами. Поэтому исследованиями этих закономерностей занимается обобщённая теория колебаний и волн. Принципиальное отличие от волн: при колебаниях не происходит переноса энергии, это, так сказать, «местные» преобразования энергии. Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса. Например, гармонически колеблется величина, изменяющаяся во времени следующим образом: x(t) = Asin(ωt + φ) или x(t) = Acos(ωt + φ),
Графики функций f(x) = sin(x) и g(x) = cos(x) на декартовой плоскости. где х — значение изменяющейся величины, t — время, остальные параметры - постоянные: А — амплитуда колебаний, ω — циклическая частота колебаний, (ωt + φ) — полная фаза колебаний, 38. Обобщенное гармоническое колебание в дифференциальном виде
(Любое нетривиальное решение этого дифференциального уравнения - есть гармоническое колебание с циклической частотой ω.) Экспоненциальная форма записи гармонических колебаний Колеблющуюся величину можно представить комплексным числом. Согласно формуле Эйлера, для комплексных чисел
Механические колебания. Пусть материальная точка совершает прямолинейные гармонические колебания вдоль оси координат
|
||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 70; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.19.26.186 (0.012 с.) |
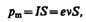 (131.1)
(131.1)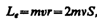 (131.2)
(131.2)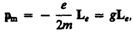 (131.3)
(131.3)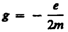 (131.4)
(131.4)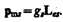 (131.5)
(131.5)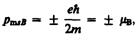

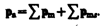 (131.6)
(131.6)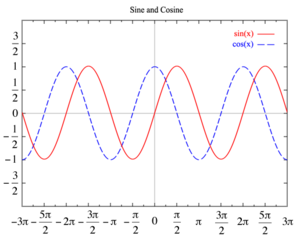

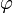 — начальная фаза колебаний.
— начальная фаза колебаний.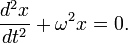
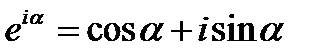 , где
, где  . Поэтому, уравнение гармонического колебания можно записать в экспоненциальной форме:
. Поэтому, уравнение гармонического колебания можно записать в экспоненциальной форме: 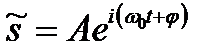 . Вещественная часть выражения
. Вещественная часть выражения 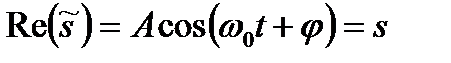 представляет собой гармоническое колебание.
представляет собой гармоническое колебание. около положения равновесия, принятого за начало координат. Тогда зависимость координаты
около положения равновесия, принятого за начало координат. Тогда зависимость координаты 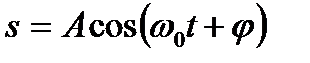 , где
, где  . Согласно выражениям
. Согласно выражениям  и
и 
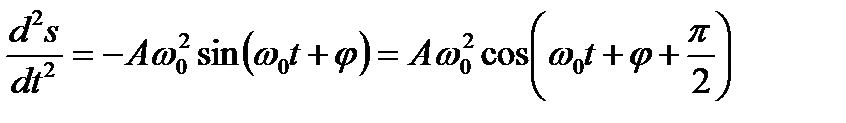 , скорость
, скорость  и ускорение
и ускорение 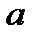 колеблющейся точки соответственно равны указанным выражениям (первая производная – скорость, вторая – ускорение). Сила
колеблющейся точки соответственно равны указанным выражениям (первая производная – скорость, вторая – ускорение). Сила 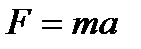 , действующая на колеблющуюся материальную точку массой
, действующая на колеблющуюся материальную точку массой 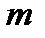 , с учётом вышеуказанных выражений, равна
, с учётом вышеуказанных выражений, равна 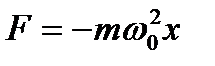 . Следовательно, сила пропорциональна смещению материальной точки из положения равновесия и направлена к противоположную сторону (к положению равновесия).
. Следовательно, сила пропорциональна смещению материальной точки из положения равновесия и направлена к противоположную сторону (к положению равновесия).


