Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непрерывная случайная величина. Закон распределения. Плотность распределения вероятностей. Числовые характеристики непрерывной случайной величины ⇐ ПредыдущаяСтр 5 из 5
Закон распределения непрерывной случайной величины
Зная плотность распределения, можно найти функцию распределения
Математическим ожиданием или средним значением непрерывной случайной величины
если этот интеграл сходится абсолютно. В противном случае математическое ожидание случайной величины Дисперсия непрерывной случайной величины определяется также, как и для дискретной случайной величины. Для непосредственного вычисления дисперсии используют формулы:
Пример Плотность распределения f (x) случайной величины X имеет вид:
Вычислить вероятность попадания случайной величины X в промежуток (2; 3). Решение. Вычислим вероятность попадания случайной величины X в промежуток (2; 3), используя формулу (23):
Ответ: Нормальное распределение Непрерывная случайная величина имеет нормальное или гауссовское распределение с параметрами
для любого При Если случайная величина
Найти вероятность попадания случайной величины где
РЕШЕНИЕ ПРИМЕРНОГО ВАРИАНТА КОНТРОЛЬНОЙ РАБОТЫ № 6 Часть 1. Случайные события Задача 1 Производится эксперимент: бросание шестигранного игрального кубика. Исследуются возможные исходы эксперимента – события:
А – выпадение грани с четным числом точек, В – выпадение грани с числом точек, большим, чем 3, С – выпадение грани с числом точек, меньшим, чем 5. В результате одного бросания произошли все три события, т.е. произошло событие D. Выразите событие D через А, В и С. Изобразите эти события на диаграмме Эйлера-Венна. Решение. Событие D равно произведению событий А, В и С, т.к. они произошли одновременно, т. е. D = АВС. Событие D – выпадение грани с четырьмя точками.
Ответы: а) D = АВС; б) решение представлено на диаграмме. Задача 2 По каналу связи независимо друг от друга передаются три сообщения. Вероятность того, что первое сообщение будет искажено равна 0,1, второе – равна 0,2, третье – равна 0,3. Найти вероятности следующих событий: Решение. Введем в рассмотрение вспомогательные события:
Согласно условию Так как событие
Событие
причем слагаемые
Для вычисления вероятностей событий
Таким образом, окончательно получаем:
События
Ответы: Задача 3 Студент едет в университет одним из трех автобусов: № 1, № 2 или № 3. Автобус № 1 ходит в 2 раза чаще, чем № 2, а № 2 – в 3 раза реже, чем № 3. Контролеры в этих автобусах встречаются с вероятностями 0,12; 0,06 и 0,1 соответственно.
а) Следует ли студенту покупать билет стоимостью 40 руб., если штраф за безбилетный проезд составляет 500 руб.? б) В результате неудачного стечения обстоятельств студент попался контролеру. В автобусе с каким номером это скорее всего произошло? Решение. Пусть события Вероятность события В найдем по формуле полной вероятности (10)
где так называемые условные вероятности
Подставив найденные значения в формулу полной вероятности (10), получим
Таким образом, при штрафе в 500 руб. студент будет в среднем за поездку платить штраф 500.0,1= 50 руб., что при цене билета 40 руб. невыгодно. С помощью формулы Байеса оценим "апостериорные" вероятности
Таким образом, студент, скорее всего, попался контролеру в автобусе №3. Ответы: а) следует покупать билет; б) в автобусе № 3.
Задача 4 Вероятность появления события А равна 0,8 и постоянна в каждом испытании. Какова вероятность того, что при 4 испытаниях событие А произойдёт не более двух раз, если испытания независимы? Решение. Так как рассматриваются независимые испытания, в каждом из которых событие А наступает с постоянной вероятностью, то вероятность события, состоящего в том, что при n испытаниях событие А произойдёт ровно m раз можно найти, используя формулу Бернулли (12): Пусть события
Обозначим
причем слагаемые
Ответ: 0,1808. Часть 2. Случайные величины Задача 5 Стрелок ведет стрельбу по цели с вероятностью попадания при каждом выстреле 0,4. За каждое попадание он получает 5 очков, а в случае промаха очков ему не начисляют. Задание: а) составить закон распределения дискретной случайной величины б) построить многоугольник распределения, в) вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины г) найти функцию распределения Решение. а) Случайная величина 0 – если стрелок промахнулся 3 раза; 5 – если стрелок попал только один раз при трех выстрелах; 10 – если стрелок попал только 2 раза при трех выстрелах;
15 – если стрелок попал 3 раза. Так как каждый выстрел можно рассматривать, как независимое испытание, в результате которого возможны только два исхода: попадание («успех») или промах («неудача»), то вероятности, соответствующие каждому значению случайной величины, можно найти по формуле Бернулли (12):
По условию задачи имеем: число испытаний
Составим закон распределения случайной величины
б) Построим многоугольник распределения. Для этого по оси абсцисс отложим возможные значения случайной величины, а по оси ординат – соответствующие им вероятности и соединим точки (xi, pi) отрезками прямых. Полученная при этом ломаная линия и есть многоугольникраспределения вероятностей случайной величины
в) Рассчитаем числовые характеристики случайной величины Математическое ожидание вычисляем по формуле (17):
Дисперсия вычисляется по формуле (20):
Среднее квадратическое отклонение находим по формуле (22):
г) Найдем функцию распределения
если если если
если
если
На рисунке 4 представлен график функции Ответы: а) Ряд распределения случайной величины
б) многоугольник распределения – на рисунке 3, в) г) функция распределения вероятностей график функции распределения вероятностей - на рис 4. Задача 6 Непрерывная случайная Х подчинена закону распределения с плотностью f(x), причем
Требуется: найти математическое ожидание Решение. Так как все значения случайной величины Х заключены в интервале (0; 3), то:
Так как промежуток (1; 2) содержится в промежутке (0; 3), то вероятность попадания случайной величины Х в промежуток (1; 2) можно вычислить по формуле (23):
Ответ: Задача 7. Непрерывная случайная величина
Решение. Так как случайная величина
По таблице значений функции Лапласа Ответ:
ВОПРОСЫ К ЭКЗАМЕНУ 1. Классическое определение вероятности события. 2. Геометрическая вероятность события. 3. Относительная частота и статистическое определение вероятности. 4. Условная вероятность. 5. Зависимые и независимые события. Произведение событий и его свойства. Теоремы о вероятности произведения 2-х зависимых и 2-х независимых событий. 6. Совместные и несовместные события. Теоремы о вероятности суммы 2-х несовместных и 2-х совместных событий. Вероятность суммы n событий. Вероятность наступления хотя бы одного из n событий. 7. Полная группа событий. Формула полной вероятности. Вероятность гипотез (формулы Байеса). 8. Независимые испытания по схеме Бернулли. Формула Бернулли. 9. Формула Пуассона. 10. Дискретные случайные величины. Функция распределения дискретной случайной величины. 11. Числовые характеристики дискретных случайных величин. 12. Непрерывные случайные величины. Функция распределения непрерывной случайной величины. 13. Плотность распределения непрерывной случайной величины, ее свойства. 14. Математическое ожидание случайной величины, его свойства. Вычисление математического ожидания непрерывной случайной величины. 15. Дисперсия случайной величины, его свойства. Вычисление дисперсии дискретной и непрерывной случайных величин. Среднее квадратическое отклонение (СКО). 16. Нормальное распределение непрерывной случайной величины. Плотность распределения случайной величины, распределенной по нормальному закону. 17. Вероятностный смысл параметров нормального распределения случайной величины. 18. Функция распределения нормально распределенной случайной величины и ее связь с функцией Лапласа. Вероятность попадания нормально распределенной случайной величины в заданный интервал. 19. Вероятность отклонения нормально распределенной случайной величины от своего математического ожидания. Правило трех сигм. 20. Показательное распределение. Основные характеристики. 21. Равномерное распределение. Основные характеристики. Приложение 1 Таблица значений функции Гаусса
Приложение 2
Таблица значений функции Лапласа
СПИСОК ЛИТЕРАТУРЫ
[1]
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 205; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.37.120 (0.108 с.) |
 удобно задавать с помощью функции
удобно задавать с помощью функции 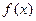 плотности распределения вероятностей. Вероятность
плотности распределения вероятностей. Вероятность  того, что значение, принятое случайной величиной
того, что значение, принятое случайной величиной 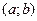 , определяется равенством:
, определяется равенством: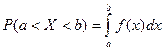 (23)
(23)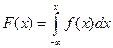 (24)
(24)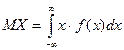 , (22)
, (22)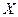 не существует.
не существует. или
или  . (23)
. (23)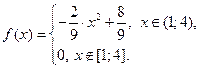



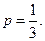
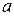 и
и 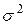 , где
, где  и
и 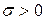 (пишут
(пишут 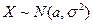 ), если функция плотности распределения вероятностей имеет вид:
), если функция плотности распределения вероятностей имеет вид: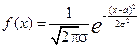 ,
,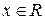 .
.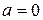 и
и 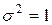 , т.е.
, т.е.  , нормальный закон распределения называется стандартным или нормированным.
, нормальный закон распределения называется стандартным или нормированным.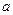 и
и 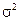 , то
, то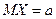 и
и 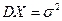 . (24)
. (24) , в интервал
, в интервал 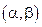 можно по формуле:
можно по формуле: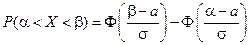 , (25)
, (25)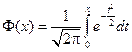 – функции Лапласа, значения которой определяются по таблице. При использовании таблицы необходимо учитывать, что функция
– функции Лапласа, значения которой определяются по таблице. При использовании таблицы необходимо учитывать, что функция 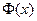 является нечетной и при
является нечетной и при 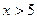 значения
значения 
 – все три сообщения переданы без искажения;
– все три сообщения переданы без искажения; 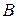 – ровно одно сообщение передано без искажения;
– ровно одно сообщение передано без искажения; 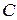 – хотя бы одно сообщение искажено.
– хотя бы одно сообщение искажено.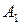 – 1-е сообщение передано без искажений,
– 1-е сообщение передано без искажений,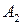 – 2-е сообщение передано без искажений,
– 2-е сообщение передано без искажений,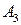 – 3-е сообщение передано без искажений,
– 3-е сообщение передано без искажений,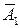 – 1-е сообщение искажено,
– 1-е сообщение искажено,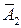 – 2-е сообщение искажено,
– 2-е сообщение искажено,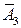 – 3-е сообщение искажено.
– 3-е сообщение искажено.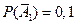 , тогда
, тогда  . Аналогично,
. Аналогично, 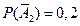 и
и 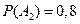 ,
,  и
и  .
.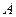 можно представить в виде
можно представить в виде 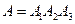 и события
и события 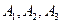 независимы, то вероятность события
независимы, то вероятность события 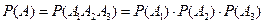
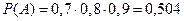 .
.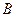 можно представить следующим образом:
можно представить следующим образом: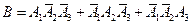 ,
,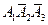 ,
, 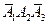 и
и 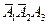 являются попарно несовместными событиями. Поэтому на основании теоремы (6) о сложении вероятностей несовместных событий получаем:
являются попарно несовместными событиями. Поэтому на основании теоремы (6) о сложении вероятностей несовместных событий получаем: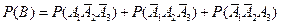 .
. ;
; ;
;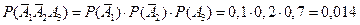 .
.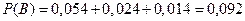 .
.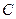 являются противоположными, следовательно,
являются противоположными, следовательно,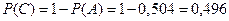 .
.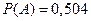 ,
, 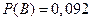 ,
,  .
.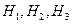 состоят в том, что студент сел в автобус № 1, № 2 или № 3 соответственно, а событие В – студент попался контролеру (все равно, в каком автобусе).
состоят в том, что студент сел в автобус № 1, № 2 или № 3 соответственно, а событие В – студент попался контролеру (все равно, в каком автобусе).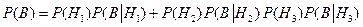 ,
,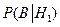 ,
,  и
и 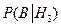 - это вероятности того, что студент был пойман контролером в автобусах № 1, № 2 или № 3. В нашей задаче эти вероятности равны 0,12; 0,06 и 0,1 соответственно. Найдем вероятности событий
- это вероятности того, что студент был пойман контролером в автобусах № 1, № 2 или № 3. В нашей задаче эти вероятности равны 0,12; 0,06 и 0,1 соответственно. Найдем вероятности событий 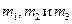 автобусов № 1, № 2, № 3. Из условия задачи
автобусов № 1, № 2, № 3. Из условия задачи 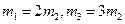 , общее число автобусов в час
, общее число автобусов в час 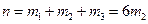 . Тогда по классическому определению вероятности, используя формулу (4), получим
. Тогда по классическому определению вероятности, используя формулу (4), получим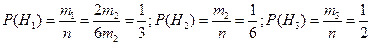 .
. .
.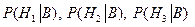 того, в каком автобусе ехал студент, если известно, что он попался контролеру.
того, в каком автобусе ехал студент, если известно, что он попался контролеру.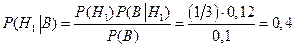 ;
;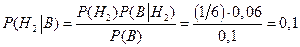 ;
;  .
.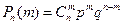 . По условию задачи имеем: число испытаний
. По условию задачи имеем: число испытаний 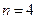 , вероятность успеха
, вероятность успеха 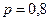 , вероятность неудачи
, вероятность неудачи 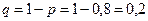 .
. состоят в том, что событие А произойдет в 4 испытаниях 0, 1, или 2 раза соответственно. Тогда:
состоят в том, что событие А произойдет в 4 испытаниях 0, 1, или 2 раза соответственно. Тогда: ;
;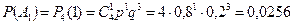 ;
;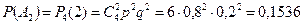 .
. ,
, , и
, и  являются попарно несовместными событиями. Поэтому на основании теоремы (6) сложения вероятностей несовместных событий получаем:
являются попарно несовместными событиями. Поэтому на основании теоремы (6) сложения вероятностей несовместных событий получаем: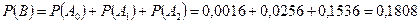 .
.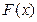 и построить ее график.
и построить ее график. .
.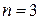 , вероятность успеха
, вероятность успеха 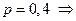
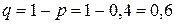 , значения
, значения 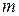 будут изменяться от 0 до 3. Рассчитаем вероятности, соответствующие каждому значению случайной величины:
будут изменяться от 0 до 3. Рассчитаем вероятности, соответствующие каждому значению случайной величины: ,
,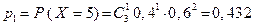 ,
,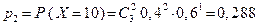 ,
,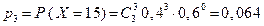 .
.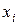

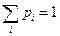

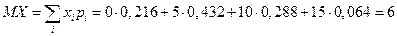 .
.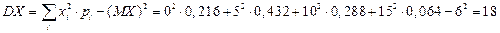 .
.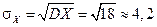 .
.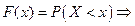
 , то
, то 
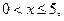 то
то 
 то
то 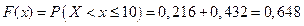 ;
;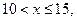 то
то 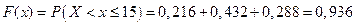 ;
;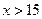 , то
, то 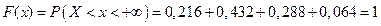

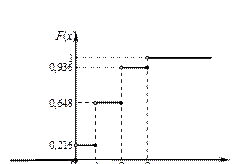 Рис. 4.
Рис. 4.
 ,
, 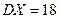 ,
, 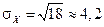 ,
,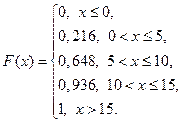

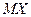 . дисперсию
. дисперсию  и вероятность попадания случайной величины Х в промежуток (1; 2).
и вероятность попадания случайной величины Х в промежуток (1; 2). ,
,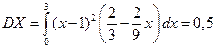 .
.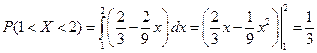 .
.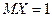 ;
; 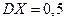 ;
; 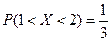 .
.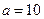 и дисперсией
и дисперсией 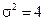 . Найти вероятность того, что в результате испытания
. Найти вероятность того, что в результате испытания 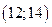 .
. ,
,  ,
, 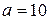 ,
, 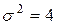 , то получим:
, то получим: .
.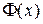 находим: F(2)=0,4772, F(1)=0,3413. Значит, получаем:
находим: F(2)=0,4772, F(1)=0,3413. Значит, получаем: 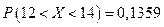 .
.