
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 5. Аппроксимация функций
Задача приближения (аппроксимации) функций заключается в том, чтобы для данной функции построить другую, отличную от нее функцию, значения которой достаточно близки к значениям данной функции. В основном аппроксимация функции применяется в случае, если: 1. Функция задана таблицей в конечном множестве точек, а вычисления нужно произвести в других точках. 2. Функция задана аналитически, но ее вычисление по формуле затруднительно. При решении задачи поиска приближенной функции возникают следующие проблемы: 1. Необходимо выбрать вид приближенной функции. Для приближения широко используются многочлены, тригонометрические функции, показательные функции и т. д. 2. Необходимо выбрать критерий близости исходной и приближенной функции. Это может быть требование совпадения обеих функций в узловых точках (задача интерполяции), минимизация среднеквадратического уклонения (метод наименьших квадратов) и др. 3. Необходимо указать правило (алгоритм), позволяющее с заданной точностью найти приближение функции. Теорема Вейерштрасса. Если функция Т.е. любую функцию можно как угодно точно аппроксимировать многочленом, но теорема ничего не говорит, ни о способах нахождения этого многочлена, ни о количестве точек, ни об их расположении. Определение аппроксимирующей функции представляет собой задание вида функции и нахождение ее коэффициентов. При аппроксимации многочленами предварительно задаются степенью многочлена и находят его коэффициенты. При этом отклонение Метод наименьших квадратов Метод наименьших квадратов–среднеквадратичное приближение функций с помощью многочлена:
На практике стараются подобрать аппроксимирующий многочлен как можно меньшей степени, обычно Мерой отклонения многочлена
Коэффициенты многочлена надо подобрать так, чтобы величина
Запишем сумму квадратов отклонений для всех точек:
Коэффициенты
Минимум функции
Эти соотношения являются системой уравнений для определения
…
Преобразуем систему и получим
…
Данная система называется системой нормальных уравнений. Для того чтобы найти коэффициенты, надо задать вид функции Линейная аппроксимация. Зададим аппроксимирующую функцию как линейную:
Подставим значения функции и производных в систему и получим:
Вынесем коэффициенты за знак суммы, получим:
Обозначим:
Тогда систему можно переписать:
Применив формулу Крамера, получим
где В итоге получаем формулу линейной аппроксимации:
Квадратичная аппроксимация. Зададим аппроксимирующую функцию в виде квадратного трехчлена:
Подставим функцию
Вынесем коэффициенты за знак суммы:
Мы получили систему линейных уравнений, поскольку в качестве аппроксимирующей функции выбрали многочлен. Если бы мы выбрали не многочлен, мы бы получили систему нелинейных уравнений. Теперь решим эту систему методом Крамера и найдем коэффициенты Для удобства можно ввести обозначения:
В этой системе все суммы ( В итоге получим формулу квадратичной аппроксимации:
Лабораторная работа 5
|
|||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 388; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.76.0 (0.012 с.) |
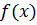 непрерывна на отрезке
непрерывна на отрезке 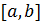 , то для любого
, то для любого 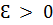 существует многочлен
существует многочлен 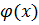 степени
степени 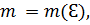 абсолютное отклонение которого от функции
абсолютное отклонение которого от функции 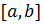 меньше
меньше  .
.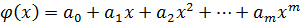 .
.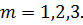
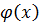 от заданной функции
от заданной функции 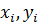 )
)  при среднеквадратичном приближении является
при среднеквадратичном приближении является 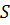 , равная сумме квадратов разностей между значениями многочлена и функции в заданных точках:
, равная сумме квадратов разностей между значениями многочлена и функции в заданных точках: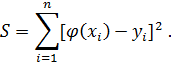
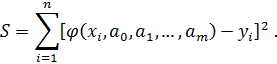
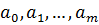 надо определить из условий минимума функции:
надо определить из условий минимума функции: .
.
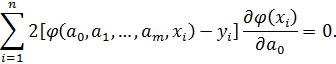


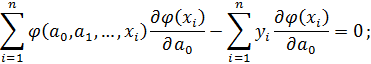
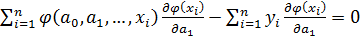 ;
;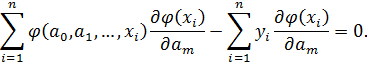
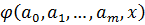 .
. ;
;
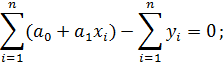

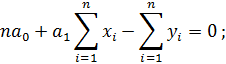
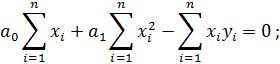
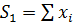 ;
;  ;
; 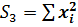 ;
;  ;
;
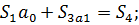

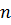 – число точек (пары
– число точек (пары  ).
).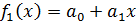 .
.

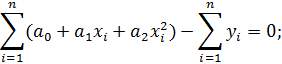
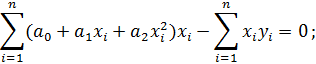
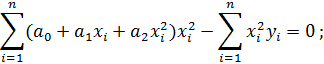
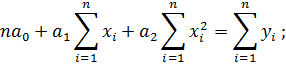
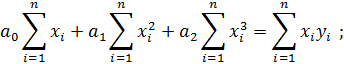

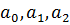 .
.
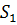 , …
, …  ) являются константами, а все неизвестные –это коэффициенты
) являются константами, а все неизвестные –это коэффициенты 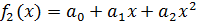 .
.


