
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Податливостей при повороте системы координат
При повороте системы координат (рис. 2.1.1) компоненты тензоров модулей упругости
Здесь Рассмотрим преобразование упругих характеристик однонаправленного композита при переходе от естественных осей координат 1-2, связанных с направлением волокон, к произвольно ориентированной системе координат x - y, полученной поворотом системы 1-2 на угол j (рис. 2.1.1). Из общего соотношения (2.1.21) формулы преобразования для
Здесь и далее: Для матрицы податливостей надо учитывать соотношения (2.1.9), что привело бы к громоздким выкладкам. Поэтому приведем лишь окончательные формулы преобразования без их вывода:
Соотношения (2.1.22) и (2.1.23) необходимы для пересчета напряжений в слоях при послойном анализе слоистых композитных пластин и оболочек (см. Лекцию 2.3 и Семинар 2.3). Отметим, что в повернутых осях материал перестает быть ортотропным (симметричным), и в отличие от (2.1.15) число констант становится равным шести, а не четырем. Правда, «плохие» константы
О задачах теории упругости Полная система уравнений теории упругости кроме определяющих соотношений (2.1.5) или (2.1.6) включает в себя уравнения совместности деформаций (2.1.26) и уравнения равновесия:
где Формулы (2.1.2) выражают 9 компонент тензора малых деформации через три компоненты вектора перемещений. Только шесть компонент деформаций считаются независимыми, как следствие из так называемого «закона парности касательных напряжений». На самом деле, это, конечно, не закон, а гипотеза, ограничивающая класс симметричной теории упругости. Развиваемые вот уже более ста лет моментные теории упругости типа Коссера эту гипотезу не используют и число компонент тензора деформаций увеличивается. Можно ввести также антисимметричный тензор вращения, компоненты которого часто предполагают пренебрежимо малыми:
Тензор
В плоском случае через две компоненты вектора перемещений надо взаимооднозначно определить три компоненты тензора деформаций, поэтому требуется одно уравнение совместности деформаций:
В трехмерном случае можно непосредственно проверить, что из 81 возможного уравнения (2.1.26) из-за симметрии по парам индексов и различия в знаках остаются независимыми только шесть: по три в каждой группе. Полагая i = k =1, j =s=2, получаем первую группу уравнений типа (2.1.27), а при i = k =1, j =2, s =3 – вторую группу:
В (2.1.27) и (2.1.28) выписаны лишь первые варианты уравнений каждой группы, по два других получаются формально – круговой перестановкой индексов 1 →2→3. Для решения задачи теории упругости необходимо задать условия на поверхности тела
В каждой точке
Таким образом, задача теории упругости состоит в решении уравнений при заданных граничных условиях. Если
|
||||||||||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 144; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.95.216 (0.006 с.) |
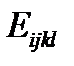 и податливостей
и податливостей 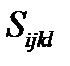 преобразуются по формулам преобразования тензора четвертого ранга:
преобразуются по формулам преобразования тензора четвертого ранга: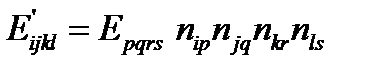 . (2.1.21)
. (2.1.21)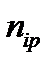 – направляющий косинус угла между осью i в новой системе координат и осью p в исходной системе. Число членов в (2.1.21) - в самом общем случае - составляет 94=6561, а с учетом симметрии тензора напряжений – 362=1296. Это к вопросу, нужно ли забивать голову студента понятием тензор или - «не экономить мел» и записывать все уравнения на доске покомпонентно. На это как раз уйдет всё время лекции. С появлением компьютеров этот вопрос отпал сам собой. Основное преимущество тензорного анализа как раз и состоит в том, что - независимо от физической природы - все тензоры преобразуются по единому правилу, которое и «зашито» в компьютерную программу. Достаточно свести величины к тензорным, а далее включается формальная процедура преобразования. Однако в матричной записи для податливостей
– направляющий косинус угла между осью i в новой системе координат и осью p в исходной системе. Число членов в (2.1.21) - в самом общем случае - составляет 94=6561, а с учетом симметрии тензора напряжений – 362=1296. Это к вопросу, нужно ли забивать голову студента понятием тензор или - «не экономить мел» и записывать все уравнения на доске покомпонентно. На это как раз уйдет всё время лекции. С появлением компьютеров этот вопрос отпал сам собой. Основное преимущество тензорного анализа как раз и состоит в том, что - независимо от физической природы - все тензоры преобразуются по единому правилу, которое и «зашито» в компьютерную программу. Достаточно свести величины к тензорным, а далее включается формальная процедура преобразования. Однако в матричной записи для податливостей 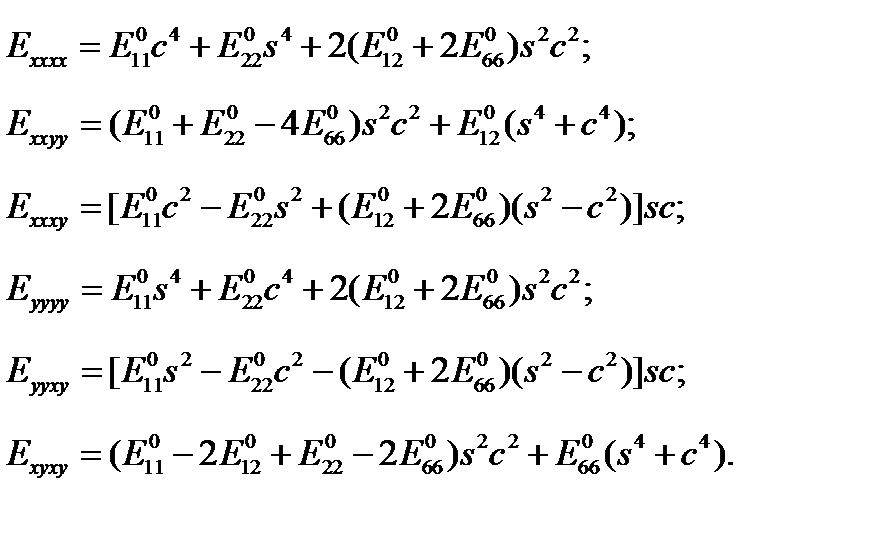 (2.1.22)
(2.1.22)
 .
.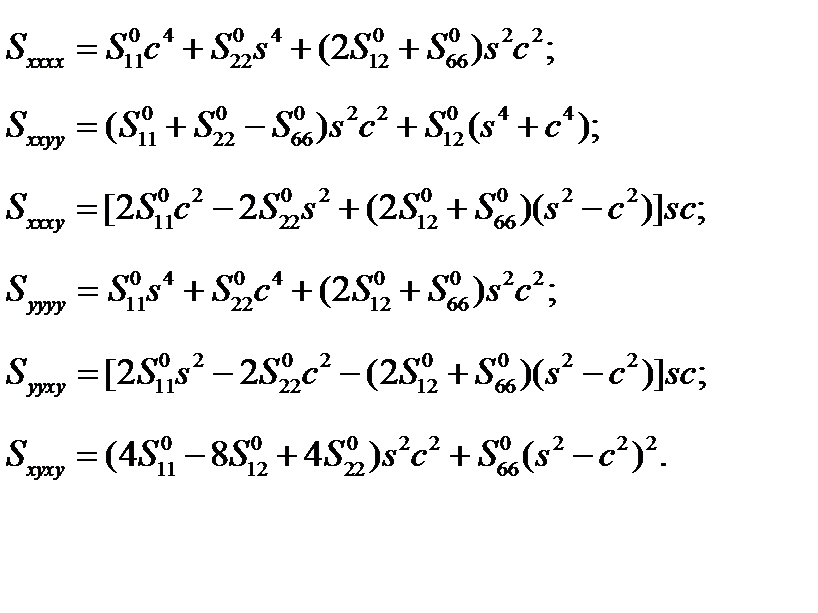 (2.1.23)
(2.1.23)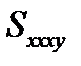 ,
,  , отвечающие за появление сдвиговых деформаций при растягивающих напряжениях (и наоборот – деформаций растяжения при сдвиге -
, отвечающие за появление сдвиговых деформаций при растягивающих напряжениях (и наоборот – деформаций растяжения при сдвиге -  ,
,  ),содержат в (2.1.22), (2.1.23)
),содержат в (2.1.22), (2.1.23) 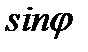 в нечетной степени, поэтому при симметричном армировании под углами +φ и –φ эти члены при сложении взаимно уничтожатся, и материал снова станет ортотропным, характеризуемым четырьмя упругими константами.
в нечетной степени, поэтому при симметричном армировании под углами +φ и –φ эти члены при сложении взаимно уничтожатся, и материал снова станет ортотропным, характеризуемым четырьмя упругими константами.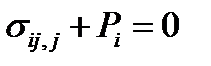 (2.1.24)
(2.1.24)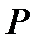 – «массовая» сила (на единицу объема),
– «массовая» сила (на единицу объема), 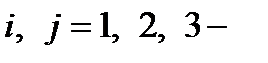 координатные оси.
координатные оси.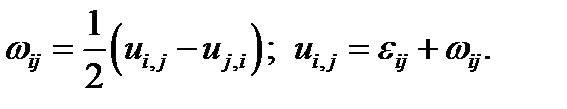
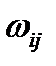 имеет три независимые компоненты: его диагональные члены равны нулю, недиагональные - антисимметричны. Чтобы обеспечить взаимооднозначное соответствие между девятью производными от трёх компонент вектора перемещений по трём координатам (или девятью компонентами тензоров (2.1.24), (2.1.25) и тремя компонентами вектора перемещений необходимо ввести шесть уравнений совместности деформаций. Их общее выражение – без вывода – имеет вид:
имеет три независимые компоненты: его диагональные члены равны нулю, недиагональные - антисимметричны. Чтобы обеспечить взаимооднозначное соответствие между девятью производными от трёх компонент вектора перемещений по трём координатам (или девятью компонентами тензоров (2.1.24), (2.1.25) и тремя компонентами вектора перемещений необходимо ввести шесть уравнений совместности деформаций. Их общее выражение – без вывода – имеет вид: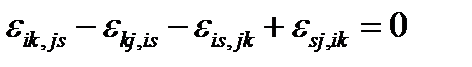 .
.
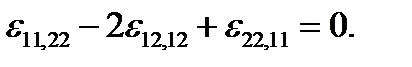
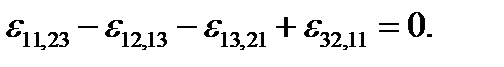
 состоящей из двух частей:
состоящей из двух частей: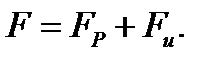 (2.1.29)
(2.1.29)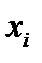 поверхности задано либо перемещение, либо распределенные усилия:
поверхности задано либо перемещение, либо распределенные усилия: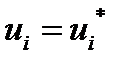 при
при 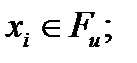 (2.1.30)
(2.1.30)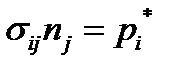 при
при 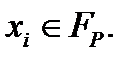 (2.1.31)
(2.1.31)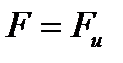 , следовательно, на всей поверхности тела заданы перемещения, соответствующая задача называется первой основной задачей теории упругости. Если
, следовательно, на всей поверхности тела заданы перемещения, соответствующая задача называется первой основной задачей теории упругости. Если 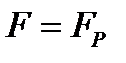 и на всей поверхности заданы распределенные усилия, будем говорить о второй основной задаче. Сформулированная выше постановка (2.1.29) - (2.1.31) относится к смешанной задаче.
и на всей поверхности заданы распределенные усилия, будем говорить о второй основной задаче. Сформулированная выше постановка (2.1.29) - (2.1.31) относится к смешанной задаче.


