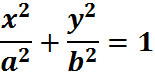Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторное поле, векторные линии.Стр 1 из 5Следующая ⇒
Введение. Предлагаемое учебное пособие предназначено студентам заочного отделения, для выполнения индивидуальных домашних заданий по курсу «Математический анализ» по следующим разделам векторного анализа: криволинейные и поверхностные интегралы второго рода. В представленном пособии кратко изложены теоретические вопросы и приведены подробные решения типовых задач, предлагаемых в качестве индивидуальных домашних заданий. Основное внимание в пособие уделено задачам на вычисление работы векторного поля; определению потенциала векторного поля; вычислению потоков векторного поля. В «Приложении» приведены варианты индивидуальных домашних заданий по вышеуказанным разделам «Математического анализа»; уравнения и вид поверхностей второго порядка, наиболее часто встречающихся в задачах; вопросы к экзамену по векторному анализу и рекомендуемая литература. Данное пособие предназначено, в основном, студентам заочного отделения для самостоятельного изучения вышеуказанных разделов курса «Математический анализ», однако, пособие может быть полезным и студентам дневного отделения при выполнении индивидуальных домашних заданий. Содержание. 1. Векторное поле, векторные линии………………………………….. 2. Криволинейный интеграл второго рода…………………………….. 2.1. Связь между криволинейными интегралами первого и второго рода………………………………………………………… 2.2. Свойства криволинейных интегралов второго рода……………….. 2.3. Физический и механический смысл криволинейного интеграла второго рода……………………………………………… 2.4. Условия независимости криволинейного интеграла второго рода от формы пути интегрирования……………………… 2.5. Оператор Гамильтона………………………………………………… 2.6. Формула Грина……………………………………………………….. 3. Поверхностный интеграл второго рода…………………………….. 3.1. Свойства поверхностных интегралов второго рода………………... 3.2. Вычисление поверхностных интегралов второго рода…………….. 3.2.1.Метод проектирования на три координатные плоскости………….. 3.2.2.Связь между поверхностными интегралами первого и второго рода………………………………………………………… 3.2.3.Метод проектирования на одну координатную плоскость……….
3.2.4.Метод Остроградского-Гаусса……………………………………... 4. Формула Стокса………………………………………………………. Приложения……………………………………………………………….. Связь между криволинейными интегралами Первого и второго рода. Пусть криволинейный интеграл второго рода по пространственной кривой АВ имеет вид:
Рассмотрим вектор-функцию F (x, y, z) = P (x, y, z) i + Q (x, y, z) j + R (x, y, z) k как трёхмерный вектор с компонентами P (x, y, z), Q (x, y, z) и R (x, y, z), а также вектор dr = dx ∙ i + dy ∙ j + dz ∙ k. Тогда комбинация, стоящая под знаком интеграла, есть не что иное, как скалярное произведение векторов P (x, y, z) dx + Q (x, y, z) dy + R (x, y, z) dz = (
Обозначим через α, β и γ углы, которые вектор
есть не что иное, как дифференциал длины дуги кривой. Поэтому
и мы можем записать
Заметим, что слева стоит криволинейный интеграл второго рода, а справа – криволинейный интеграл первого рода. Эта формула даёт связь между криволинейными интегралами первого и второго рода. 2.2. Свойства криволинейных интегралов второго рода. 1. Постоянный множитель выносится за знак криволинейного интеграла
Свойства криволинейных интегралов второго рода будем рассматривать на одной из составляющих криволинейного интеграла. 2. Криволинейный интеграл от суммы функции равен сумме интегралов
3. Если кривая AB разбивается точкой С на две части, то
4. Криволинейный интеграл второго рода по замкнутой кривой (циркуляция) не зависит от выбора начальной точки, а зависит только от направления обхода данной кривой. 5. Если AB – кривая, лежащая в плоскости, перпендикулярной оси OX, то
Если дуга AB принадлежит плоскости, перпендикулярной оси OY, то
если дуга AB лежит в плоскости, перпендикулярной оси OZ, то
Оператор Гамильтона Многие операции векторного анализа могут быть записаны в сокращенной и удобной для расчетов форме путем введения символического дифференцирующего вектора набла Ротором вектора (2.7)
Если Пример: вычислить потенциальную функцию плоского векторного поля Решение начнем с нахождения
Следовательно, поле
Проверка:
Кроме ротора векторного поля с помощью символического вектора набла можно найти градиент скалярной функции Скалярное произведение вектора
Формула Грина. Для достаточно общего вида плоских областей D с положительно ориентированной границей Г справедлива формула Грина:
Формула Грина позволяет вычислить криволинейный интеграл второго рода по замкнутой линии Г, т.е. циркуляцию через двойной интеграл по области D, ограниченной этой кривой линией. Пример: вычислить циркуляцию вектора
по окружности Циркуляция данного вектора равна:
Находим частные производные:
Тогда по формуле Грина (2.10):
Т.к. кривая L является окружностью, то при вычислении двойного интеграла используем полярную систему координат: Тогда
Пример: пользуясь формулой Грина, вычислить линейный интеграл в векторном поле
Уравнение окружности: или сдвинут по оси Ох вправо на одну единицу. Дополним дугу полуокружности отрезком прямой ОА. Кривая ОАО – становится замкнутой. Тогда по формуле Грина (2.10):
По свойству двойного интеграла полученный интеграл равен площади области D, а радиус полуокружности R=1. Интеграл вдоль прямой ОА равен нулю (на ОА у=0; dy=0), следовательно, окончательный ответ - линейный интеграл равен
Формула Стокса Формула Стокса связывает криволинейный и поверхностный интегралы второго рода. Пусть в некоторой области пространства задано поле непрерывно дифференцируемого вектора
Выше мы уже определили понятие ротора вектора вектора поля
Тогда по формуле Стокса:
Циркуляция вектора Предполагается, что ориентация нормали
Формула Стокса позволяет вычислять криволинейные интегралы второго рода по замкнутым контурам с помощью поверхностных интегралов второго рода. Пример: вычислить циркуляцию вектора L: x 2 + y 2 =4 при z =3; вычисления провести двумя способами: а) непосредственно; б) по формуле Стокса. x 2 + y 2 =4 – круговой цилиндр, радиуса R =2 с образующей, параллельной оси OZ. Контур L - окружность, лежащая в плоскости z =3.
а) Параметрические уравнения линии L: x= 2cos t; y=2sint; z=3; 0 ≤ t ≤ 2π dx= -2sint dt; dy= 2cost dt; dz=0
Вычисляем криволинейный интеграл второго рода. Тогда:
б) Вычисления по формуле Стокса начнем с определения ротора векторного поля:
Вектор нормали к плоскости z =3 Тогда, по формуле Стокса:
При вычислении интеграла воспользовались полярными координатами (x =ρ cos Пример: найти циркуляцию векторного поля длина нормали Вычислим ротор векторного поля в соответствии с формулой (2.7):
Вычислим скалярное произведение ротора вектора поля и единичной нормали:
Следовательно, по формуле Стокса (4.1):
Приложения. Варианты индивидуальных заданий. Вариант № 1. 1) Вычислить потенциальную функцию векторного поля.
2) Вычислить работу векторного поля силы Ғ(М) при движении материальной точки по заданному пути L:
L: ломаная ABCD, AC // OX, CD // OX, DB // OY. A (0, 1, 2), B (1, -1, 3) 3) Вычислить поток векторного поля через заданную поверхность в указанном направлении:
Поверхность замкнутая, нормаль внешняя.
Вариант № 2. 1) Вычислить потенциальную функцию векторного поля.
2) Вычислить работу векторного поля силы Ғ(М) при движении материальной точки по заданному пути L:
От точки M (2, 0) до точки N (0, 0).
3) Вычислить поток векторного поля через заданную поверхность в направлении внешней нормали.
Вариант № 3.
1) Вычислить потенциальную функцию векторного поля.
2) Вычислить работу векторного поля силы Ғ(М) при движении материальной точки по заданному пути L:
L: замкнутый контур, полученный пересечением поверхности
3) Вычислить поток векторного поля через заданную замкнутую поверхность в сторону внешней нормали.
Вариант № 4.
1) Вычислить потенциальную функцию векторного поля.
2) Вычислить работу векторного поля силы Ғ(М) при движении материальной точки по заданному пути L:
3) Вычислить поток векторного поля через замкнутую поверхность в сторону внешней нормали.
Вариант № 5. 1) Вычислить потенциальную функцию векторного поля.
2) Вычислить работу векторного поля силы Ғ(М) при движении материальной точки по заданному пути L:
3) Вычислить поток векторного поля через заданную поверхность в указанном направлении.
S: часть поверхности
Вариант № 6. 1) Вычислить потенциальную функцию векторного поля.
2) вычислить работу векторного поля силы Ғ(М) при движении материальной точки по заданному пути L:
L:
3) Вычислить поток векторного поля через заданную поверхность в указанном направлении:
S: часть поверхности
P: Вариант № 7.
1) Вычислить потенциальную функцию векторного поля.
2) Вычислить работу векторного поля силы Ғ(М) при движении материальной точки по заданному пути L:
L: контур треугольника ABC, где вершины треугольника имеют следующие координаты A (1; 0; 0), B (0; 1; 0), C (0; 0; 1).
3) Вычислить поток векторного поля через заданную поверхность в указанном направлении.
S: часть плоскости
Вариант № 8.
1) Вычислить потенциальную функцию векторного поля.
2) Вычислить работу векторного поля силы Ғ(М) при движении материальной точки по заданному пути L:
L:
3) Вычислить поток векторного поля через замкнутую поверхность в направлении внешней нормали:
Вариант № 9. 1) Вычислить потенциальную функцию векторного поля.
2) Вычислить работу векторного поля силы Ғ(М) при движении материальной точки по заданному пути L:
L: замкнутый контур
3) Вычислить поток векторного поля через заданную поверхность в указанном направлении.
S: часть поверхности
Вариант № 10. 1) Вычислить потенциальную функцию векторного поля.
2) Вычислить работу векторного поля силы Ғ(М) при движении материальной точки по заданному пути L:
L: замкнутый контур
3) Вычислить поток векторного поля через заданную поверхность в указанном направлении.
S: часть поверхности
Вариант № 11.
1) Вычислить потенциальную функцию векторного поля.
2) Вычислить работу векторного поля силы Ғ(М) при движении материальной точки по заданному пути L.
L: замкнутый контур
3) Вычислить поток векторного поля через заданную поверхность в указанном направлении.
S: часть поверхности
Вариант № 12.
1) Вычислить потенциальную функцию векторного поля.
2) Вычислить работу векторного поля силы Ғ(М) при движении материальной точки по заданному пути L.
L: отрезок AB, соединяющий точки A (1, 2, -2) и B (-2, 1, 4).
3) Вычислить поток векторного поля через заданную поверхность в указанном направлении.
S: часть поверхности
Вариант № 13. 1) Вычислить потенциальную функцию векторного поля.
2) Вычислить работу векторного поля силы Ғ(М) при движении материальной точки по заданному пути L:
L: замкнутый контур x2+(y-1)2=1, обход в положительном направлении. 3) Вычислить поток векторного поля через часть плоскости S: x /3 + y +2 z =1 расположенную в первом октанте, в направлении внешней нормали. Вариант № 14. 1) Вычислить потенциальную функцию векторного поля.
2) Вычислить работу векторного поля силы Ғ(М) при движении материальной точки по заданному пути L.
L: x2+y2+z2=4, z = 1, (y≥0) от точки M(√3;0;1) до точки N (-√3;0;1).
3) Вычислить поток векторного поля через замкнутую поверхность в направлении внешней нормали.
S:
Вариант № 15. 1) Вычислить потенциальную функцию векторного поля.
2) Вычислить работу векторного поля силы Ғ(М) при движении материальной точки по заданному пути L.
L: замкнутый контур 3) Вычислить поток векторного поля через замкнутую поверхность S S: Вариант № 16. 1) Вычислить потенциальную функцию векторного поля.
2) Вычислить работу векторного поля силы Ғ(М) при движении материальной точки по заданному пути L.
L: контур треугольника, ограниченного осями координат и прямой
3) Вычислить поток векторного поля через замкнутую поверхность S
S: Вариант № 17. 1) Вычислить потенциальную функцию векторного поля.
2) Вычислить работу векторного поля силы Ғ(М) при движении материальной точки по заданному пути L:
L: замкнутый контур 3) Вычислить поток векторного поля через замкнутую поверхность в направлении внешней нормали:
S: Вариант № 18. 1) Вычислить потенциальную функцию векторного поля.
2) Вычислить работу векторного поля силы Ғ(М) при движении материальной точки по заданному пути L:
L: контур треугольника OAB, где O(0,0,0), A(1,0,0), B(1,1,2). 3) Вычислить поток векторного поля через замкнутую поверхность в направлении внешней нормали:
S:
Вариант № 19. 1) Вычислить потенциальную функцию векторного поля.
2) Вычислить работу векторного поля силы Ғ(М) при движении материальной точки по заданному пути L:
L: x2+y2=1, (y≥0) от точки M(1;0) до точки N (-1;0). 3) Вычислить поток векторного поля через замкнутую поверхность в направлении внешней нормали:
S: Вариант № 20. 1) Вычислить потенциальную функцию векторного поля.
2) Вычислить работу векторного поля силы Ғ(М) при движении материальной точки по заданному пути L:
L: 3) Вычислить поток векторного поля через замкнутую поверхность в направлении внешней нормали:
S:
Вариант № 21. 1) Вычислить потенциальную функцию векторного поля.
2) Вычислить работу векторного поля силы Ғ(М) при движении материальной точки по заданному пути L (контур замкнутый):
L: 3) Вычислить поток векторного поля через заданную поверхность в направлении внешней нормали:
S: Вариант № 22. 1) Вычислить потенциальную функцию векторного поля.
2) Вычислить работу векторного поля силы Ғ(М) при движении материальной точки по заданному пути L (контур замкнутый):
L: 3) Вычислить поток векторного поля через заданную поверхность (первый октант) в направлении внешней нормали:
S:
Вариант № 23. 1) Вычислить потенциальную функцию векторного поля.
2) Вычислить работу векторного поля силы Ғ(М) при движении материальной точки по заданному пути L (замкнутый контур):
L: 3) Вычислить поток векторного поля через заданную поверхность в направлении внешней нормали
S: Вариант № 24. 1) Вычислить потенциальную функцию векторного поля.
2) Вычислить работу векторного поля силы Ғ(М) при движении материальной точки по заданному пути L:
L: 3) Вычислить поток векторного поля через поверхность S в направлении внешней нормали:
S: часть плоскости находящаяся в I октанте.
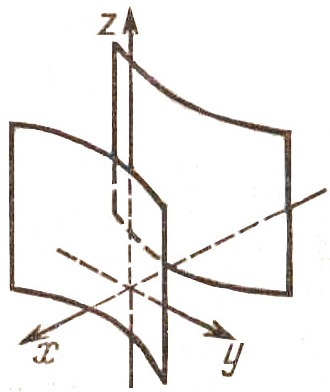
Гиперболоид двуполостный
Введение. Предлагаемое учебное пособие предназначено студентам заочного отделения, для выполнения индивидуальных домашних заданий по курсу «Математический анализ» по следующим разделам векторного анализа: криволинейные и поверхностные интегралы второго рода. В представленном пособии кратко изложены теоретические вопросы и приведены подробные решения типовых задач, предлагаемых в качестве индивидуальных домашних заданий. Основное внимание в пособие уделено задачам на вычисление работы векторного поля; определению потенциала векторного поля; вычислению потоков векторного поля. В «Приложении» приведены варианты индивидуальных домашних заданий по вышеуказанным разделам «Математического анализа»; уравнения и вид поверхностей второго порядка, наиболее часто встречающихся в задачах; вопросы к экзамену по векторному анализу и рекомендуемая литература. Данное пособие предназначено, в основном, студентам заочного отделения для самостоятельного изучения вышеуказанных разделов курса «Математический анализ», однако, пособие может быть полезным и студентам дневного отделения при выполнении индивидуальных домашних за
|
|||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 141; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.61.187 (0.4 с.) |
 P (x, y, z) dx + Q (x, y, z) dy + R (x, y, z) dz
P (x, y, z) dx + Q (x, y, z) dy + R (x, y, z) dz (x, y, z) и
(x, y, z) и 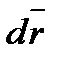 , т.е.
, т.е.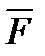 (x,y,z)
(x,y,z)  ), и поэтому
), и поэтому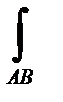 P (x, y, z) dx + Q (x, y, z) dy + R (x, y, z) dz =
P (x, y, z) dx + Q (x, y, z) dy + R (x, y, z) dz = 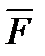 (x,y,z),
(x,y,z), 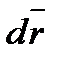 ).
).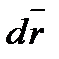 образует с осями OX, OY и OZ. Заметим, что длина вектора
образует с осями OX, OY и OZ. Заметим, что длина вектора  :
: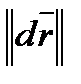 =
= 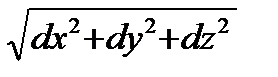 = ds
= ds dx = ds ∙ cosα, dy = ds ∙ cosβ, dz = ds ∙ cosγ
dx = ds ∙ cosα, dy = ds ∙ cosβ, dz = ds ∙ cosγ Pdx =
Pdx = 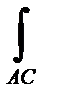 Pdx +
Pdx + 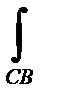 Pdx
Pdx , называемого оператором Гамильтона.
, называемого оператором Гамильтона.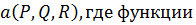
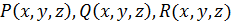 и их первые частные производные непрерывны в некоторой области 3-х мерного пространства, называется вектор, получаемый в результате векторного произведения символического вектора
и их первые частные производные непрерывны в некоторой области 3-х мерного пространства, называется вектор, получаемый в результате векторного произведения символического вектора 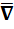 и вектора
и вектора 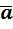 .
.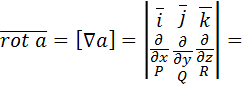
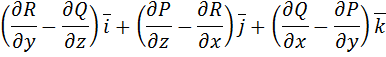
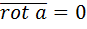 , то векторное поле
, то векторное поле 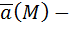 потенциально, т.к. если координаты вектора
потенциально, т.к. если координаты вектора 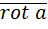 равны нулю, то мы получаем условия потенциальности векторного поля (2.5). Потому в задачах на нахождение потенциальной функции при проверке условий потенциальности векторного поля можно использовать либо условия потенциальности (2.5), либо вычислять
равны нулю, то мы получаем условия потенциальности векторного поля (2.5). Потому в задачах на нахождение потенциальной функции при проверке условий потенциальности векторного поля можно использовать либо условия потенциальности (2.5), либо вычислять 
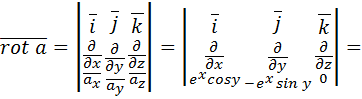
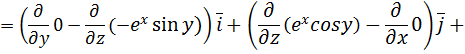

 является потенциальным. Найдем потенциальную функцию, используя формулу (2.6):
является потенциальным. Найдем потенциальную функцию, используя формулу (2.6):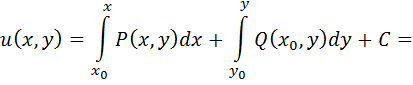


 , путем простого умножения вектора набла на скалярную функцию
, путем простого умножения вектора набла на скалярную функцию 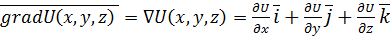 (2.8)
(2.8)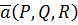 называется дивергенцией векторного поля. Дивергенция – величина скалярная и вычисляется следующим образом:
называется дивергенцией векторного поля. Дивергенция – величина скалярная и вычисляется следующим образом: (2.9)
(2.9)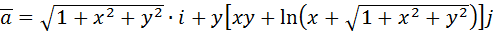
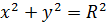

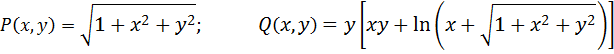
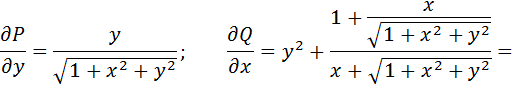
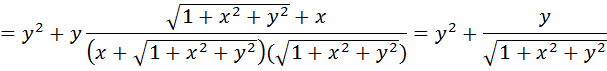
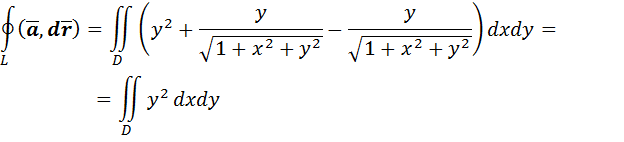

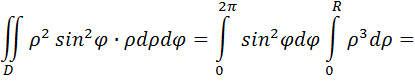
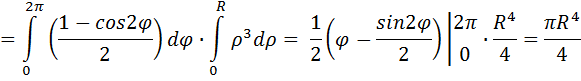
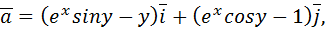 где L - верхняя часть полуокружности
где L - верхняя часть полуокружности 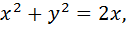 направление обхода контура от точки A (2;0) до точки О(0;0)
направление обхода контура от точки A (2;0) до точки О(0;0)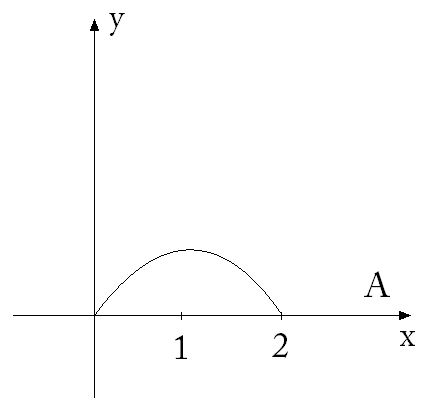
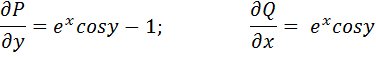
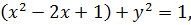
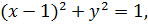 т.е. центр окружности рис. 2.4
т.е. центр окружности рис. 2.4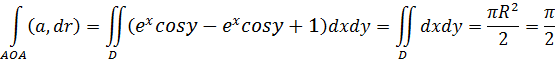
 .
.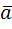 = P(x,y,z)
= P(x,y,z)  +Q(x,y,z)
+Q(x,y,z) 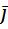 +R(x,y,z)
+R(x,y,z) 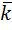
 как векторного произведения символического вектора набла
как векторного произведения символического вектора набла 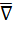 =
= 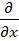
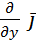 +
+  и
и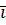 + Q
+ Q 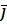 + R
+ R 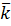
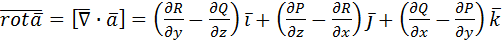
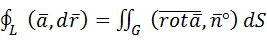 (4.1)
(4.1)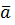 по любому замкнутому контуру L равна потоку ротора этого вектора
по любому замкнутому контуру L равна потоку ротора этого вектора  к поверхности G согласована с ориентацией контура L таким образом, чтобы из конца нормали обход контура в выбранном направлении был виден совершающимся против часовой стрелки. Формулу Стокса можно трактовать как обобщение формулы Грина для пространственного случая. В координатной форме формула Стокса имеет вид:
к поверхности G согласована с ориентацией контура L таким образом, чтобы из конца нормали обход контура в выбранном направлении был виден совершающимся против часовой стрелки. Формулу Стокса можно трактовать как обобщение формулы Грина для пространственного случая. В координатной форме формула Стокса имеет вид: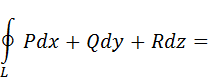
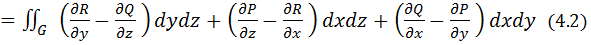
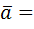 y
y 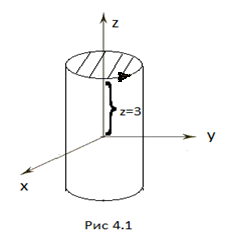 Выберем ориентацию дуги L как указано на рис.4.1.
Выберем ориентацию дуги L как указано на рис.4.1.

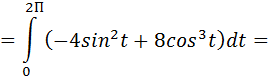

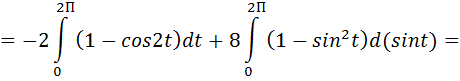

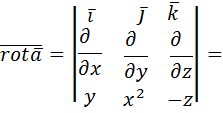

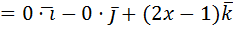
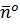 (0;0;1)
(0;0;1)



 , y =ρ sin
, y =ρ sin 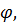 якобиан равен ρ).
якобиан равен ρ).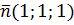 ,
,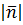 =
=  , тогда единичная нормаль, сонаправленная с данной имеет координаты
, тогда единичная нормаль, сонаправленная с данной имеет координаты 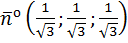 .
.


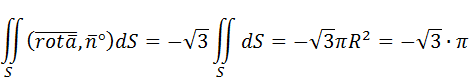

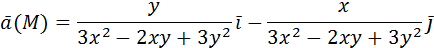
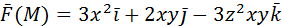
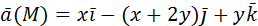



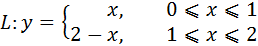
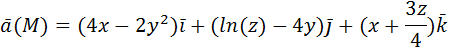
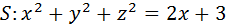
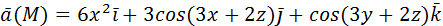
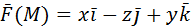
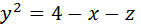 координатными плоскостями.
координатными плоскостями.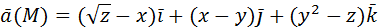
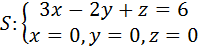
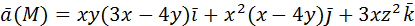
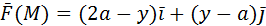
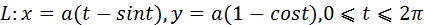
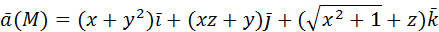
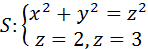

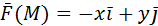

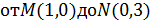
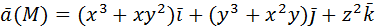
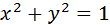 , вырезаемая плоскостями
, вырезаемая плоскостями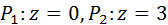 , нормаль внешняя по отношению к замкнутой поверхности.
, нормаль внешняя по отношению к замкнутой поверхности.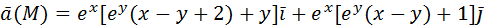

 от точки M (3, 0) до точки N (-3, 0).
от точки M (3, 0) до точки N (-3, 0).
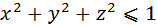 , вырезаемая плоскостью
, вырезаемая плоскостью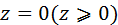 , нормаль внешняя.
, нормаль внешняя.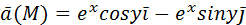
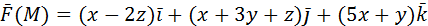
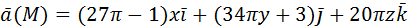
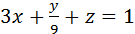 , расположенная в 1 октанте, нормаль положительная.
, расположенная в 1 октанте, нормаль положительная.

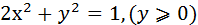 , от точки M
, от точки M 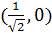 , до точки N
, до точки N 
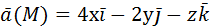
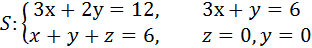
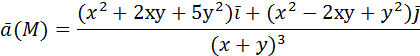
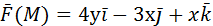
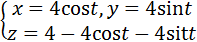

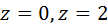 нормаль внешняя по отношению к замкнутой поверхности.
нормаль внешняя по отношению к замкнутой поверхности.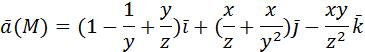


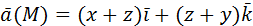
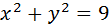 , отсекается плоскостями
, отсекается плоскостями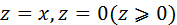 , нормаль внешняя.
, нормаль внешняя.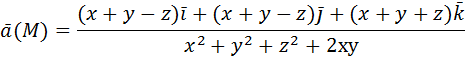

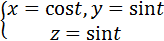

 , отсекаемая плоскостью
, отсекаемая плоскостью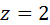 , нормаль внешняя.
, нормаль внешняя.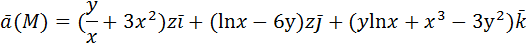
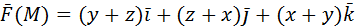
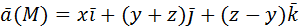
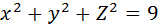 , отсекаемая плоскостью
, отсекаемая плоскостью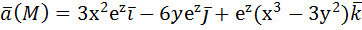
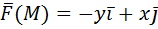
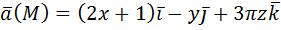
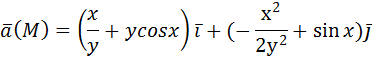
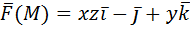
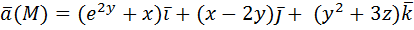
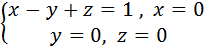
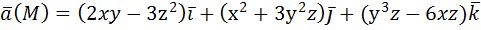
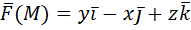
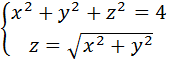
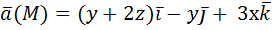
 нормаль внешняя.
нормаль внешняя.

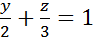

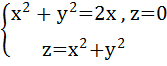 , нормаль внешняя
, нормаль внешняя 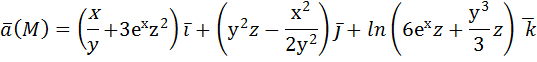
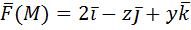
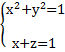 (обход из точки 0(0,0,0) виден совершающимся против часовой стрелки).
(обход из точки 0(0,0,0) виден совершающимся против часовой стрелки).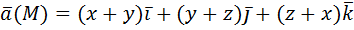
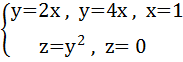

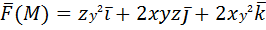
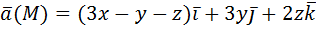

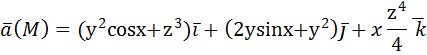
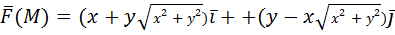

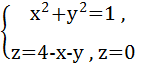

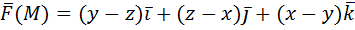
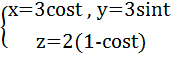 , 0≤t≤2
, 0≤t≤2 
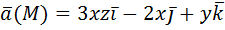

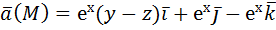
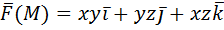
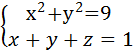
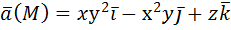
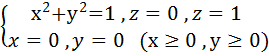


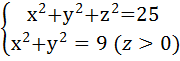
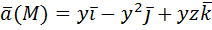
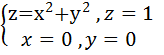
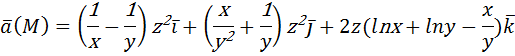

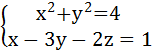


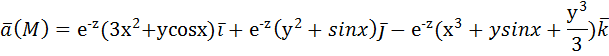
 , 0≤t≤2
, 0≤t≤2 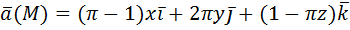
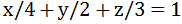 ,
,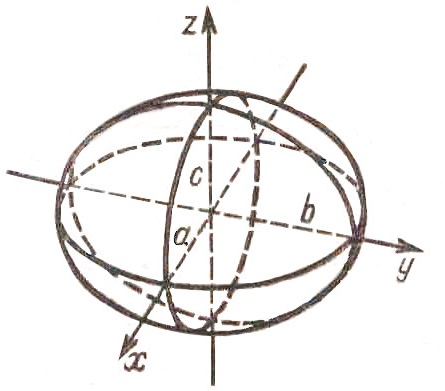 Эллипсоид
Эллипсоид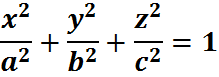

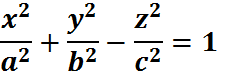

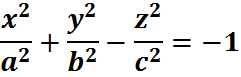
 Конус второго порядка
Конус второго порядка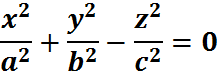
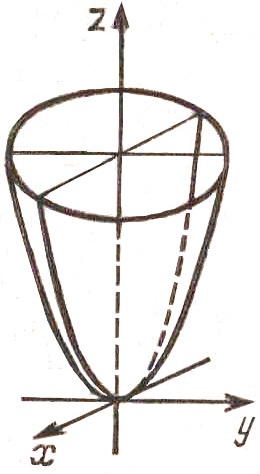 Параболоид эллиптический
Параболоид эллиптический
 Параболоид гиперболический
Параболоид гиперболический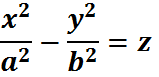
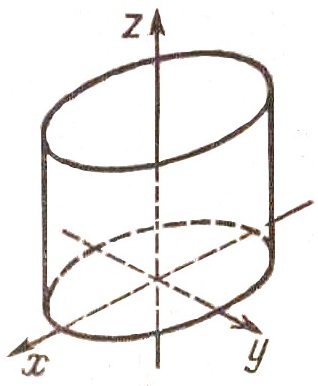 Эллиптический цилиндр второго порядка
Эллиптический цилиндр второго порядка