Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ортогональное проецирование прямой линииСодержание книги
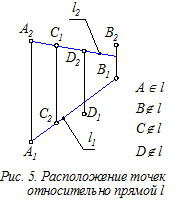
Поиск на нашем сайте 4.1. Общие понятия и определения. Прямая в пространстве и на ортогональном чертеже может быть задана: а) двумя точками; б) точкой и направлением прямой; в) двумя пересекающимися плоскостями. Определение. На эпюре точка лежит на прямой, если её проекции расположены на одноимённых проекциях этой прямой (рис. 5).
В рассматриваемом разделе производится оценка проекционных свойств прямых в зависимости от их расположения относительно плоскостей проекции П1, П2 и П3. При этом прямые в основном задаются лишь двумя своими проекциями (горизонтальной и фронтальной).
Проекционные свойства (ПС) прямых общего положения – длина прямых и углы их наклона к плоскостям проекций на ортогональном чертеже искажены, т. е. показаны не в натуральную величину.
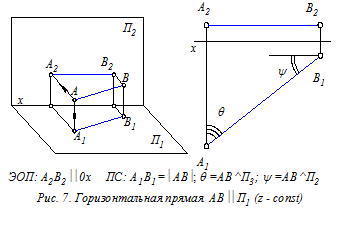
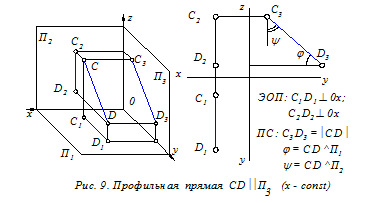
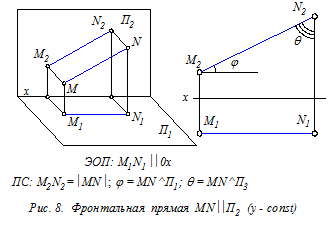
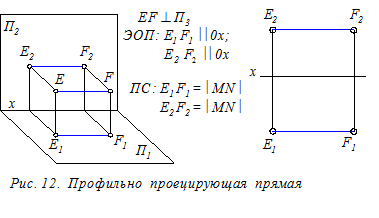
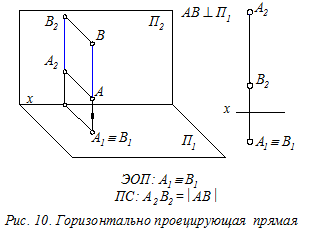
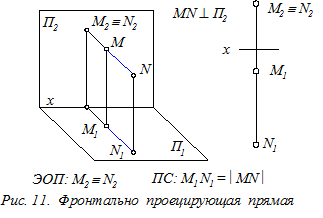
Прямые уровня (рис. 7 - 9) – это прямые, расположенные параллельно одной из плоскостей проекций (П1, П2 или П3). ПС прямых уровня: на указанную плоскость проекций такие прямые отображаются в натуральную величину. Кроме этого на эту плоскость без искажения проецируются и углы наклона прямых к двум другим плоскостям проекций. ЭОП прямых уровня: одна из заданных проекций прямой уровня параллельна координатной оси (0х или 0 z). Это означает, что одна из трёх координат любой точки прямой уровня постоянна (т.е. не изменяется). Прямые проецирующие – это прямые, расположенные перпендикулярно одной из плоскостей проекций (П1, П2 или П3). На указанную плоскость такие прямые проецируются вырожденно, в виде точки (рис.10 - 12). На две другие плоскости проекций прямые отображаются в натуральную величину, т. к. они параллельны этим плоскостям. Определение. Вырожденной проекцией прямой называется точка ортогонального чертежа, где отобразились все точки этой прямой. Вырожденная проекция прямойобладает собирательным свойством: проекции всех точек прямой расположены в одной точке чертежа.
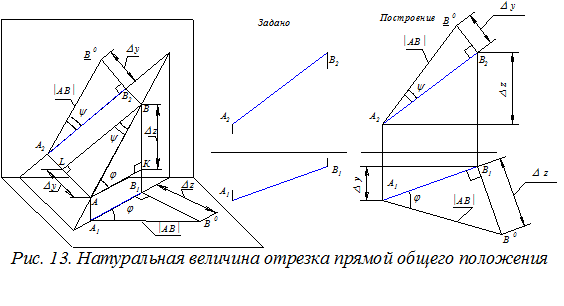
Прямые уровня и проецирующие прямые называются прямыми частного положения. Рассмотрев различные положения прямой относительно плоскостей проекций можно сформулировать следующее правило: Если на ортогональном чертеже (эпюре) одна из двух заданных проекций прямой параллельна координатной оси или вырождается в точку, то на другой проекции прямая отобразилась в натуральную величину. 4.3. Определение натуральной величины отрезка прямой общего положения и углов наклона этой прямой к плоскостям проекций На эпюре задан отрезок АВ (А1В1, А2В2) прямой общего положения (рис. 13). Требуется графически определить его длину и углы наклона к плоскостям проекций П1 и П2.
Правило. Для определения натуральной величины (| АВ |) отрезка прямой общего положения и углов (j и y) наклона прямой к плоскостям проекций П1 и П2 необходимо построить прямоугольные треугольники А1В1В0 и А2В2 В 0 (см. рис. 13), используя в качестве первого катета одну из двух заданных проекций прямой (А1В1 или А2В2). Длину второго катета определить как разность (D z или D y) удалений концов другой проекции прямой от координатной оси. Тогда гипотенуза построенного треугольника определит НВ отрезка (| АВ |), а угол между гипотенузой и исходной проекцией прямой определит угол наклона прямой к соответствующей плоскости проекций.
|
|||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 347; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 4.2. Расположение прямой относительно плоскостей проекций
4.2. Расположение прямой относительно плоскостей проекций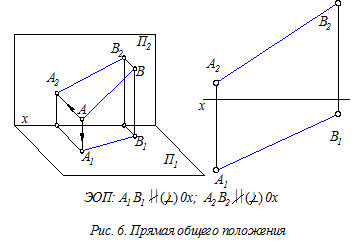 Прямая общего положения – это прямая, не перпендикулярная ни одной из плоскостей проекций (П1, П2 или П3). Эпюрный опознавательный признак (ЭОП) прямых общего положения – обе заданные проекции прямых непараллельны и неперпендикулярны к координатным осям (рис. 6).
Прямая общего положения – это прямая, не перпендикулярная ни одной из плоскостей проекций (П1, П2 или П3). Эпюрный опознавательный признак (ЭОП) прямых общего положения – обе заданные проекции прямых непараллельны и неперпендикулярны к координатным осям (рис. 6).