
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ортогональное проецирование точки на три плоскости проекцийСтр 1 из 8Следующая ⇒
Принятые обозначения
а) А Î(Ï) l – точка А принадлежит (не принадлежит) прямой l; б) l Ì(Ë) α – прямая l принадлежит (не принадлежит) плоскости α; в) l ' А – прямая l проходит через точку А; г) α É l – плоскость α проходит через прямую l.
Предмет НГ Начертательная геометрия (НГ) изучает способы построения плоских изображений геометрических объектов. В курсе НГ обычно рассматриваются следующие разделы: 1. Построение и преобразование ортогональных чертежей (эпюр) геометрических фигур; 2. Проекции с числовыми отметками; 3. Линейная перспектива. В настоящем конспекте будет рассмотрен первый раздел: способы построения и преобразования эпюр следующих геометрических фигур: точка, прямая, плоскость, многогранная и кривая поверхность. Изучение этих способов будет иллюстрироваться решением позиционных, метрических и конструктивных задач. Позиционные задачи – это задачи на взаимное расположение, принадлежность или пересечение геометрических фигур (например, построение отрезка, лежащего в плоскости, параллельного или перпендикулярного плоскости, взаимное пересечение двух плоскостей, кривых поверхностей и. т.п.). Метрические задачи – это задачи по определению линейных или угловых размеров геометрических фигур, а также расстояний между ними (например, определение длины отрезка прямой и углов наклона этой прямой к плоскостям проекций, определение натуральной величины (НВ) плоского или двугранного угла, определение НВ сечения многогранника (кривой поверхности) плоскостью и др.).
Конструктивные задачи – построение геометрических фигур по заданным условиям. Способы проецирования В основе построения изображений объектов лежит их проецирование на плоскость проекций (картину). В НГ рассматриваются два способа проецирования: центральное и параллельное проецировани е.
В зависимости от ориентации вектора S по отношению к плоскости П различают: а) ортогональное (прямоугольное) проецирование, если S ^ П (этот метод будет использоваться далее как основной инструмент для построения ортогональных чертежей); б) косоугольное проецирование, если S Свойства параллельных проекций: 1. Проекцией прямой есть прямая или точка. Проекция прямой в виде точки называется вырожденной проекцией прямой. Она возникает, если проецируемая прямая параллельна направлению проецирования S. 2. Если точка расположена на прямой, то проекция этой точки расположена на проекции прямой. 3. Если прямые параллельны, то параллельны и их проекции. 4. Отношение длин отрезков прямой равно отношению длин проекций этих отрезков. Главные линии плоскости К главным линиям плоскости относятся прямые, лежащие в плоскости и параллельные одной из плоскостей проекций, а также линии наибольшего наклона (ЛНН) к этим плоскостям проекций.
При решении позиционных и метрических задач на плоскости обычно используются следующие главные линии плоскости: горизонталь, фронталь плоскости, а также ЛНН к плоскостям проекций П1 и П2. Таких линий можно построить на чертеже множество. Горизонталь (h) плоскости (рис. 30) – это прямая, лежащая в плоскости и параллельная горизонтальной плоскости проекций (П1). Для построения горизонтали плоскости общего положения используют ЭОП горизонтальных прямых: h2 || 0х. Фронталь (f) плоскости (см. рис. 30) – это прямая, лежащая в плоскости и параллельная фронтальной плоскости проекций (П2). Для построения фронтали плоскости общего положения используют ЭОП фронтальных прямых: f1 || 0х.
Свое название (ЛНН) такая прямая получила потому, что из множества (пучка) прямых, проведенных через точку А на плоскости a, именно такая прямая имеет наибольший угол (j) наклона к плоскости проекций П1. Линией ската такая прямая называется потому, что тело (например, шарик), помещённое в точку А и предоставленное самому себе, под воздействием силы тяжести будет перемещаться (скатываться) в плоскости a по прямой АВ. ЛНН к плоскости П2 – это линия плоскости, перпендикулярная к фронталям плоскости и определяющая угол наклона плоскости к плоскости проекций П2. Кривые поверхности 8.1. Основные понятия и определения Кривая поверхность F может быть образована перемещением в пространстве линии l или поверхности S, которые называются образующими этой поверхности. В общем случае линия l может быть пространственной кривой произвольной формы, а поверхность S - произвольной кривой поверхностью. Если линия l является прямой линией, то формируемая с её помощью поверхность называется линейчатой. Если линия l является окружностью, то формируемая с её помощью поверхность называется циклической. Для задания способа перемещения в пространстве образующей линии (или поверхности) вводятся понятия: - направляющей линии – это линия, по которой перемещается одна из точек образующей линии (или поверхности); - плоскость параллелизма – это плоскость, параллельно которой всегда находится образующая линия в своём пространственном перемещении; - ось вращения – это прямая линия, относительно которой происходит поворот образующей линии (или поверхности). -линия центров циклической поверхности – это в общем случае пространственная кривая, на которой всегда находится центр образующей окружности в процессе своего пространственного перемещения. Для построения изображений кривых поверхности на ортогональном чертеже и решения позиционных задач на этих поверхностях используется понятие каркаса поверхности - совокупности линий, расположенных на этой поверхности таким образом, что в общем случае через любую её точку проходит лишь одна линия каркаса. С точки зрения математики каркас поверхности представляет семейство родственных линий, у которых изменяется лишь один из множества параметров (например, радиус окружности, одна из трёх координат и т.п.), с помощью которых может описываться рассматриваемая поверхность.
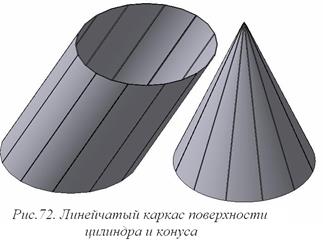
В общем случае на кривой поверхности можно построить множество семейств линий каркаса и среди этого множества интерес представляют простейшие каркасы: линейчатый (рис. 72) или циклический (рис. 73). Каркас считается непрерывным, если его линии можно провести через любую точку кривой поверхности (сфера, тор, цилиндр, конус, косая плоскость и др.) или дискретным, если на поверхности можно провести ограниченное число линий каркаса (поверхность земли, поверхность крыла и фюзеляжа самолёта, поверхность корпуса судна и др.).
Геометрическая часть определителя (ГЧ) – это набор геометрических элементов (точка, прямая, плоскость и т. п.), с помощью которых может быть построен каркас поверхности.
Алгоритмическая часть определителя (АЧ) – формальная последовательность действий с элементами, входящими в ГЧ определителя, позволяющая построить каркас поверхности. На рис. 74 показаны каркас и определитель цилиндрической и конической поверхностей. Принятые обозначения
а) А Î(Ï) l – точка А принадлежит (не принадлежит) прямой l; б) l Ì(Ë) α – прямая l принадлежит (не принадлежит) плоскости α; в) l ' А – прямая l проходит через точку А; г) α É l – плоскость α проходит через прямую l.
Предмет НГ
Начертательная геометрия (НГ) изучает способы построения плоских изображений геометрических объектов. В курсе НГ обычно рассматриваются следующие разделы: 1. Построение и преобразование ортогональных чертежей (эпюр) геометрических фигур; 2. Проекции с числовыми отметками; 3. Линейная перспектива. В настоящем конспекте будет рассмотрен первый раздел: способы построения и преобразования эпюр следующих геометрических фигур: точка, прямая, плоскость, многогранная и кривая поверхность. Изучение этих способов будет иллюстрироваться решением позиционных, метрических и конструктивных задач. Позиционные задачи – это задачи на взаимное расположение, принадлежность или пересечение геометрических фигур (например, построение отрезка, лежащего в плоскости, параллельного или перпендикулярного плоскости, взаимное пересечение двух плоскостей, кривых поверхностей и. т.п.). Метрические задачи – это задачи по определению линейных или угловых размеров геометрических фигур, а также расстояний между ними (например, определение длины отрезка прямой и углов наклона этой прямой к плоскостям проекций, определение натуральной величины (НВ) плоского или двугранного угла, определение НВ сечения многогранника (кривой поверхности) плоскостью и др.). Конструктивные задачи – построение геометрических фигур по заданным условиям. Способы проецирования В основе построения изображений объектов лежит их проецирование на плоскость проекций (картину). В НГ рассматриваются два способа проецирования: центральное и параллельное проецировани е.
В зависимости от ориентации вектора S по отношению к плоскости П различают: а) ортогональное (прямоугольное) проецирование, если S ^ П (этот метод будет использоваться далее как основной инструмент для построения ортогональных чертежей); б) косоугольное проецирование, если S Свойства параллельных проекций: 1. Проекцией прямой есть прямая или точка. Проекция прямой в виде точки называется вырожденной проекцией прямой. Она возникает, если проецируемая прямая параллельна направлению проецирования S.
2. Если точка расположена на прямой, то проекция этой точки расположена на проекции прямой. 3. Если прямые параллельны, то параллельны и их проекции. 4. Отношение длин отрезков прямой равно отношению длин проекций этих отрезков. Ортогональное проецирование точки на три плоскости проекций Рассмотрим три взаимно перпендикулярные плоскости проекций: П1 – горизонтальная, П2 – фронтальная и П3 – профильная, пересечение которых образует прямоугольную систему координат 0 xyz (рис. 3).
Выполнив проецирование точки А на все три плоскости П1, П2 и П3, получим соответственно горизонтальную (А1), фронтальную (А2) и профильную (А3) проекции точки А. Если спроецировать точку А на координатные оси 0 x, 0 y, 0 z (точки А x, А y, Az соответственно), то можно определить координаты точки А в рассматриваемой системе. Такими координатами будут отрезки: хА=0Ах, уА=0АУ, zA=0 Az. В рассматриваемом случае точка А(хА, yА, zА) пространства имеет проекции А1 (хА, yА), Любые две ортогональные проекции точки однозначно определяют положение точки в пространстве и на чертеже, т.к. используют все три координаты точки. Поэтому в дальнейшем, при решении задач НГ геометрические фигуры будут задаваться двумя своими проекциями. Кроме этого отметим геометрический смысл прямоугольных координат точки: Координата точки определяет удаление этой точки от соответствующей плоскости проекций (например, координата zА – удаление точки А от плоскости П1, координата уА – это удаление точки А от плоскости П2,, а координата хА - от плоскости П3). Если точка имеет одну нулевую координату, то она лежит на одной из плоскостей проекции. Если точка имеет две нулевые координаты, то она лежит на одной из координатных осей. Переход от пространственной модели проецирования точки А (см. рис. 3) к её ортогональному чертежу (эпюру) – рис. 4 осуществляется путём совмещения в единую плоскость трёх плоскостей проекций П1, П2 и П3. (плоское преобразование Г. Монжа) При этом на эпюре не присутствует геометрический объект - точка А, но показываются её проекции.
Определение. Эпюром (ортогональным чертежом) точки называется изображение, содержащее две проекции точки, расположенные на линии связи, перпендикулярной координатной оси (рис. 4, а) При переходе от пространственной модели проецирования точки А к её эпюру в системе трёх плоскостей проекций (рис. 4, б) надо иметь ввиду следующие обстоятельства: 1. Каждая и координатных осей является наложением двух осей. 2. Координата точки А на эпюре определяется расстоянием от проекции точки до соответствующей координатной оси (см. рис. 4).
|
||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 78; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.247.196 (0.054 с.) |
 ,
, 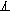 - знаки перпендикулярности (неперпендикулярности).
- знаки перпендикулярности (неперпендикулярности). ,
, 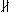 - знаки параллельности (непараллельности).
- знаки параллельности (непараллельности). - знак скрещивающихся прямых.
- знак скрещивающихся прямых.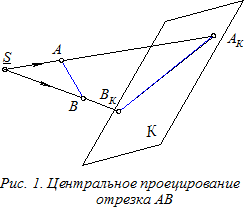 Центральное проецирование простейшего геометрического объекта – точки А осуществляется путем проведения луча из точки S, называемой центром проецирования, через заданную точку А до пересечения его в точке АК с плоскостью картины К. На рис. 1 показана центральная проекция АКВК отрезка АВ. Центральное проецирование рассматривается в разделе НГ - Линейная перспектива, где изучаются способы построения на картине реальных объектов (объектов природы, улиц, зданий и сооружений, интерьеров комнат и др.).
Центральное проецирование простейшего геометрического объекта – точки А осуществляется путем проведения луча из точки S, называемой центром проецирования, через заданную точку А до пересечения его в точке АК с плоскостью картины К. На рис. 1 показана центральная проекция АКВК отрезка АВ. Центральное проецирование рассматривается в разделе НГ - Линейная перспектива, где изучаются способы построения на картине реальных объектов (объектов природы, улиц, зданий и сооружений, интерьеров комнат и др.).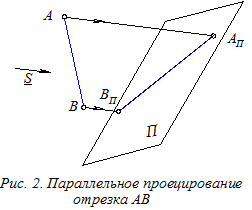 Параллельное проецирование точки А осуществляется путём проведения через неё прямой параллельно направлению проецирования S (рис. 2). Точка АП пересечения такой прямой с плоскостью проекций П называется параллельной проекцией точки А.
Параллельное проецирование точки А осуществляется путём проведения через неё прямой параллельно направлению проецирования S (рис. 2). Точка АП пересечения такой прямой с плоскостью проекций П называется параллельной проекцией точки А. ЛНН к плоскости проекций П1 (по-другому именуемая линией ската)– это линия плоскости, перпендикулярная к горизонталям плоскости и определяющая угол наклона этой плоскости к плоскости проекций П1 (см. на рис. 30 прямую АВ и угол j).
ЛНН к плоскости проекций П1 (по-другому именуемая линией ската)– это линия плоскости, перпендикулярная к горизонталям плоскости и определяющая угол наклона этой плоскости к плоскости проекций П1 (см. на рис. 30 прямую АВ и угол j).
 Задание кривой поверхности может быть осуществлено определителем поверхности - совокупностью условий, однозначно определяющих поверхность в пространстве и на чертеже. Рассматривают геометрическую и алгоритмическую части определителя.
Задание кривой поверхности может быть осуществлено определителем поверхности - совокупностью условий, однозначно определяющих поверхность в пространстве и на чертеже. Рассматривают геометрическую и алгоритмическую части определителя.
 Определение. Ортогональной проекцией точки А на плоскость проекций П1 называется основание перпендикуляра (А1), проведённого из точки А на указанную плоскость проекций.
Определение. Ортогональной проекцией точки А на плоскость проекций П1 называется основание перпендикуляра (А1), проведённого из точки А на указанную плоскость проекций.



