
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: соотношение неопределенностей Гейзенберга. Уравнение Шредингера.
Основные формулы
Методические указания Гипотеза Планка утверждает, что излучение и поглощение света происходит не непрерывно, а дискретно, т.е определенными порциями (квантами). Энергия кванта определяется частотой ν: Для микрочастицы одновременно невозможно точно определить и величину координату и импульса, а неопределенности этих величин подчиняются соотношению неопределенностей Гейзенберга. Соотношение неопределенностей Гейзенберга является квантовым ограничением применимости классической механики к микрообъектам. Состояние микрочастиц в квантовой механике описывается с помощью волновой функции Y, которая является основным носителем информации об их корпускулярных и волновых свойствах. Примеры решения задач Пример №1. Определить неопределенность Δх в определении координаты электрона, движущегося в атоме водорода со скоростью ν = 1.5*106 м/с, если допускаемая неопределенность Δν в определении скорости составляет 10 % от ее величины.
Ответ: Δх = 0.77 м
Пример №2. Электрон находится в бесконечно глубоком одномерном потенциальном ящике (яме) шириной L = 0.5 нм на первом энергетическом уровне. Найти вероятность нахождения электрона в интервале L / 4, равно удаленном от стенок ящика.
х1 = L/2 – L/8 = 3*L/8; х2 = L/2 + L/8 = 5*L/8. Нормированная собственная волновая функция, описывающая состояние электрона в потенциальном ящике, имеет вид:
Т.к по условию задачи n = 1, то
Получим:
Преобразуем, произведя замену для вычисления интеграла:
и разобьем на два интеграла:
Проведем расчет:
Ответ: W = P = 0,2485 ≈ 0,249.
Пример №3. Электрон проходит через прямоугольный потенциальный барьер шириной d = 0.5 нм Высота барьера U больше энергии Е электрона на 1%. Вычислить коэффициент прозрачности D если энергия электрона Е = 100 эВ.
Ответ: D = 6.5*10-3.
Пример №4. Частица находится в одномерной прямоугольной "потенциальной яме" шириной l с бесконечно высокими "стенками". Запишите уравнение Шредингера в пределах "ямы" 0 ≤ Х ≤ l и решите его.
Ответ:
Пример №5. Частица с энергией Е движется в положительном направлении оси х и встречает на своем пути бесконечно широкий прямоугольный барьер высотой U, причем Е <U. Принимая А1 = 1 и используя условия непрерывности волновой функции и ее первой производной на границе областей 1 и 2, определить плотность вероятности | Ψ2(0) | 2 обнаружения частицы в точке х = 0 области 2.
1 + B1 = A2, k1 - B1 k1 = A2k2 B1 = A2 – 1, k1 – (A2 – 1) k1 = A2k2 2 k1 = (k1 + k2)A2, A2 = 2 k1 / k1 + k2
Ответ:
Пример №6. Волновая функция, описывающая состояние частицы в одномерной "потенциальной яме" с бесконечно высокими "стенками", имеет вид Ψ(x) = Asinkx. Определите: 1) вид собственной волновой функции Ψ n (x); 2) коэффициент А, исходя из условия нормировки вероятностей.
Ответ: 1) Ψ n (x) = A sin n π / l * x; 2)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 285; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.143.207 (0.038 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 ;
;
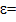 hω
hω
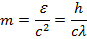
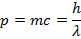

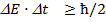
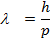
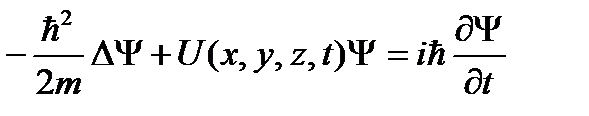 , где Ψ = Ψ(x, y, z, t) – волновая функция, описывающая состояние частицы;
ħ = h / 2 π;
m - масса частицы;
Δ - оператор Лапласа (ΔΨ = ∂2Ψ / ∂x2 + ∂2Ψ / ∂y2 + ∂2Ψ / ∂z2);
, где Ψ = Ψ(x, y, z, t) – волновая функция, описывающая состояние частицы;
ħ = h / 2 π;
m - масса частицы;
Δ - оператор Лапласа (ΔΨ = ∂2Ψ / ∂x2 + ∂2Ψ / ∂y2 + ∂2Ψ / ∂z2);
 - мнимая единица;
U = U(x, y, z, t) - потенциальная энергия частицы в силовом поле, в котором она движется.
- мнимая единица;
U = U(x, y, z, t) - потенциальная энергия частицы в силовом поле, в котором она движется.
 ,
,
 | Ψ |2dV = 1,
где интегрирование производится по всему бесконечному пространству, т. е. по координатам x, y, z от - ∞ до + ∞.
| Ψ |2dV = 1,
где интегрирование производится по всему бесконечному пространству, т. е. по координатам x, y, z от - ∞ до + ∞.
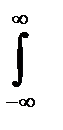 | Ψ(x)|2dx.
| Ψ(x)|2dx.
 L | Ψ |2dV.
L | Ψ |2dV.
 , где A – амплитуда волны де Бройля;
px = k ħ - импульс частицы;
E = ħ ω - энергия частицы.
, где A – амплитуда волны де Бройля;
px = k ħ - импульс частицы;
E = ħ ω - энергия частицы.
 , (n = 1, 2, 3, …). где l – ширина ямы.
, (n = 1, 2, 3, …). где l – ширина ямы.
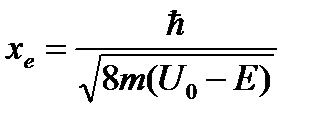 .,
.,
 ,
,
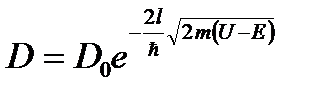 ,
гдеD0– множитель, который можно приравнять единице;
U- высота потенциального барьера;
E - энергия частицы.
,
гдеD0– множитель, который можно приравнять единице;
U- высота потенциального барьера;
E - энергия частицы.
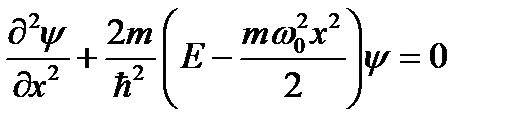 ,
где (m* ω02 * x2) / 2 = U– потенциальная энергия осциллятора;
ω0- собственная частота колебаний осциллятора;
m - масса частицы.
,
где (m* ω02 * x2) / 2 = U– потенциальная энергия осциллятора;
ω0- собственная частота колебаний осциллятора;
m - масса частицы.


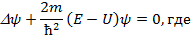

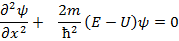

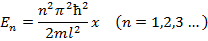
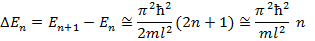
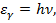 где h- постоянная Планка.
где h- постоянная Планка.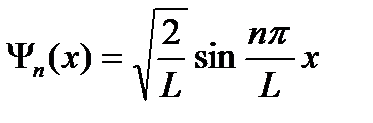 .
. .
. .
.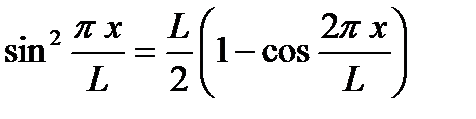 ,
, .
.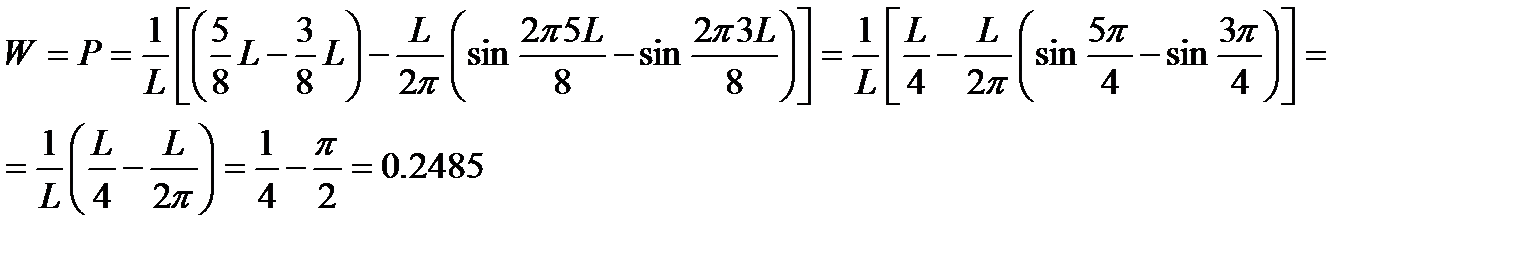
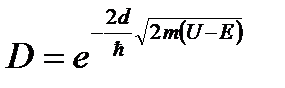 .
.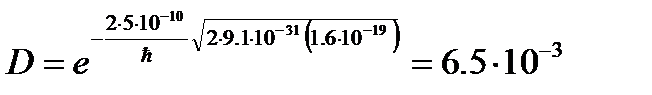 .
.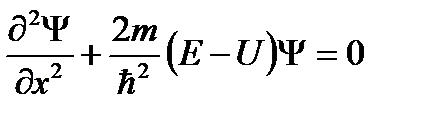 .
. .
. ,
, .
.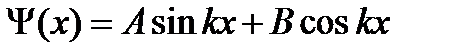 .
. , B = 0,
, B = 0, 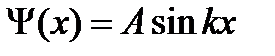 ,
, 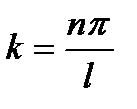 ,
,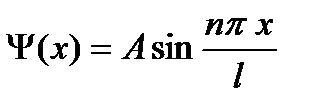 .
.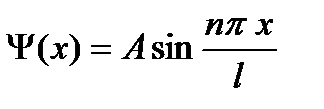 .
. ,
,  .
.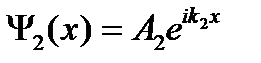 ,
,  .
. ,
, ,
, ,
, 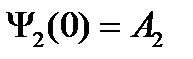 .
. ,
, 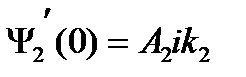

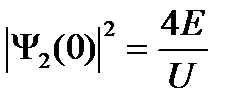 .
. | Ψ n (x) |2 dx = 1,
| Ψ n (x) |2 dx = 1,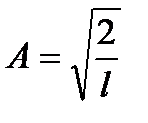 .
.


