Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула полной вероятности. Формула Байеса.Стр 1 из 6Следующая ⇒
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное автономное образовательное учреждение высшего образования «Национальный исследовательский Нижегородский государственный университет им. Н.И. Лобачевского»
АВТОРЫ
СБОРНИК ЗАДАЧ ПО ДИСЦИПЛИНЕ «ТЕОРИЯ ВЕРОЯТНОСТЕЙ» Учебно-методическое пособие Рекомендовано методической комиссией Института экономики и предпринимательства ННГУ для студентов для специальностей 38.03.02 «Менеджмент», 38.03.02 «Экономика» и 38.03.003 «Управление персоналом»
Нижний Новгород 2019 г. УДК 372.851 ББК 74.262.21 Сборник задач по дисциплине «ТЕОРИЯ ВЕРОЯТНОСТЕЙ» Авторы: ………….. учебно-методическое пособие. - Нижний Новгород: Нижегородский госуниверситет, 2019. - с.
Рецензент: ………………………………………………………………… Учебно-методическое пособие «Сборник задач по дисциплине «Теория вероятностей», для студентов специальностей 38.03.02 «Менеджмент (по отраслям?)», 38.03.02 «Экономика» и 38.03.003 «Управление персоналом» на базе основного общего образования. В каждом разделе, оно содержит краткое теоретическое введение и примеры решения типовых задач. Ответственный за выпуск: председатель методической комиссии Института экономики и предпринимательства, Летягина Е.Н.
УДК 372.851 ББК 74.262.21 АВТОРЫ
© Нижегородский государственный университет им. Н.И. Лобачевского, 2019
Содержание Введение …………………………………………………………………………4 Раздел 1. Предмет теории вероятностей, основные понятия и зада-чи ………………………………………………………………………………….5 1.1 Вероятности случайного события. Классическое определение вероятности. Элементы комбинаторики.………………………………………… 7 1.2 Действия над событиями………………………………………………..………. 10 1.2.1 Сумма событий……………………………….. …………………………10 1.2.2 Разность событий………………………………….………………………. 11 1.2.3 Произведение событий……………………………………………………... 11 1.3 Условная вероятность. Теорема умножения вероятностей. Независимые события…………………………………………………………………………………… 12 1.4 Формула полной вероятности. Формула Байеса…………………………….. 15 1.5 Задачи для самостоятельного решения………………………………….……. 17
Раздел 2. Повторные независимые испытания. Приближенные форму-лы для расчета вероятности ………………………………………….…………… 23 2.1 Формула Бернулли……………………….………………………………………….. 23 2.2 Формула Пуассона……………………………………………………………….... 24 2.3 Формулы Муавра-Лапласа……………………………………………….……….. 24 2.4 Наивероятнейшее число появления событий…………………………….…... 25 2.5 Задачи для самостоятельного решения ………………………………………. 27
Раздел 3 Случайные величины …………………………………………………..… 32 3.1 Дискретные случайные величины. Функция распределения…………...…… 32 3.2 Законы распределения дискретных случайных величин…………………….. 34 3.3. Числовые характеристики дискретных случайных величин……………...37 3.4 Задачи для самостоятельного решения……………………………………….. 39 3.5 Непрерывные случайные величины и их числовые характеристики……... 48 3.6 Задачи для самостоятельного решения……………………………………………………………………………………. 50
Раздел 4 Закон больших чисел …………………………………………………….. 58 4.1 Неравенство Маркова……………………………………………………………... 58 4.2 Неравенство Чебышева…………………………………………………………… 58 4.3 Теорема Чебышева…………………………………………………………………. 58 4.4 Теорема Бернулли..…………………………………………………………………. 59 4.5 Центральная предельная теорема…………………………………………..59 4.6 Задачи для самостоятельного решения……………………………………….. 62 Приложение……………………………………………………………………………… 69 Информационное обеспечение обучения…………………………………………… 71 Введение К настоящему времени, опубликовано довольно большое количество учебников и различных методических пособий, посвященных такой математической дисциплине как т еория вероятностей. Однако, при работе над ними, авторы брали за основу рабочие программы, разработанные для конкретных направлений подготовки специалистов в конкретных учебных заведениях. При работе над настоящим пособием, основная цель преследуемая авторами состояла в том, чтобы создать сборник контрольных заданий с краткими теоретическими пояснениями, с учетом специфики подготовки студентов заочной формы обучения на экономическом факультете Нижегородского государственного университета, с конкретной ориентацией на рабочие программы по таким специальностям как Менеджмент (38.03.02), Экономика (38.03.01) и Управление персоналом (38.03.03).
Пособие состоит из четырех разделов, каждый из которых включает в себя краткое изложение теоретического материала, примеры решения типовых задач и задач предназначенных для самостоятельного решения. Последние, брались из материалов, используемых авторами при подготовке настоящей рукописи, что отмечено путем приведения соответствующих ссылок указанных после каждого номера задачи в квадратных скобках. Кроме того, пособие содержит Приложение с табличными значениями функций необходимых для решения ряда задач, а также списки требуемой для освоения материала обязательной и дополнительной литературы с указанием соответствующих Интернет-ресурсов. Раздел 1. Предмет теории вероятностей, ее основные понятия и задачи Теория вероятностей это математическая наука, изучающая закономерности в явлениях (событиях) с неопределенным исходом, которые при неограниченном воспроизведении одного и того же испытания (опыта) каждый раз протекают несколько по-иному. Ее основными понятиями являются элементарное событие и пространство элементарных событий. Под элементарным событием следует понимать появление или наоборот непоявление того или иного исхода испытания. Пространство элементарных событий представляет собой множество, каждому элементу которого соответствует один исход испытания. Подмножество пространства элементарных событий принято называть случайным событием, которое в результате испытания может произойти или не произойти (выпадение цифры при подбрасывании монеты, звонок по сотовому телефону в данную минуту и т. д.). Именно математические модели случайных событий и представляют предмет исследования теории вероятностей. Задачи теории вероятностей, в первую очередь, заключаются в том, чтобы осуществлять научный прогноз различных явлений за счет предвидения вероятностей предшествующих им других более сложных явлений. Кроме того, с помощью теории вероятностей осуществляется количественная оценка влияния различных случайных факторов на результат какого-либо конкретного испытания. Последнее, представляет интерес для экспериментаторов, с точки зрения изучения возможности оказания влияния на конечный результат этого испытания. Каждое из событий обладает той или иной степенью возможности появления, которая (количественно) характеризуется его вероятностью. Событие считается достоверным, если в результате опыта оно обязательно должно произойти. (выпадение одной из шести граней при бросании игральной кости). Его вероятность равна единице. Противоположным достоверному событию считается событие невозможное, которое не может произойти в данном опыте (выпадение десяти очков при бросании игральной кости). Его вероятность равна нулю. В том случае, если вероятность события не равна нулю но близка к нему, данное событие принято называть практически невозможным. А если вероятность не равна единице, но близка к ней – практически достоверным.
Если в результате осуществления какого-либо опыта, одно из нескольких событий обязательно должно произойти, то считается что последние образуют полную группу событий. В качестве примера можно привести обязательное появление 1, 2, 3, 4, 5 или 6 очков при бросании игральной кости. При этом, вполне понятно, что любые два из событий (например, одновременное появление «2» и «5» очков) не могут произойти одновременно. Такие события и им подобные принято называть несовместными. Если можно считать, что ни одно из всех возможных событий появляющихся в результате испытания, не является объективно более возможным чем другие (как в случае появления определенного количества очков при бросании игральной кости), то такие события принято называть равновозможными и считать что данное испытание (опыт) обладает симметрией и «сводится к схеме случаев».
1.1. Вероятность случайного события. Классическое определение вероятности Элементы комбинаторики. Как известно, каждое испытание завершается некоторым исходом (результатом) или событием. Для обозначения событий используются заглавные буквы латинского алфавита A, B, C,…. Каждое из них, как уже отмечалось выше, обладает какой-то степенью возможности своего появления. Числовая мера этой возможности, например какого-либо события A, представляет собой не что иное как вероятность его появления и обозначается символом В том случае если А – достоверное событие, то Пример 1. Игральную кость подбрасывают один раз. Найти вероятность событий: А – появление четного числа очков; В – появление не менее пяти очков; С – появление не более пяти очков. Решение. Испытание имеет шесть равновозможных независимых исходов (появление одного, двух, трех, четырех, пяти или шести очков), образующих полную систему. Из них, событию А благоприятствуют три исхода (выпадение двух, четырех и шести очков), поэтому
При вычислении вероятности, часто приходится использовать формулы комбинаторики – раздела математики, который изучает, в частности, методы решения дискретных (комбинаторных) задач, т.е. задач на подсчет числа различных комбинаций. Если выборки (комбинации) из В том случае, если в перестановках из общего числа Если выборки из В случае, когда некоторые элементы (или все) могут оказаться одинаковыми, то такие сочетания называются сочетаниями с повторениями из Выборки из Если некоторые элементы (или все) могут оказываются одинаковыми, то такие размещения называются размещениями с повторениями из Рассмотрим конкретные примеры непосредственного вычисления вероятностей. Пример 2. В урне находится 7 красных и 6 синих шаров. Из урны одновременно вынимают два шара. Какова вероятность того, что оба шара красные (событие А)? Решение. Общее число равновозможных независимых исходов равно
Событию А благоприятствуют Пример 3. В партии из 24 деталей пять бракованных. Из партии выбирают наугад 6 деталей. Найти вероятность того, что среди этих 6 деталей окажутся 2 бракованных (событие В). Решение. Общее число равновозможных независимых исходов равно
Число исходов Среди шести взятых наугад деталей должно быть 2 бракованных и 4 стандартных. Две бракованные детали из пяти можно выбрать
Пример 10. Девять различных книг расставлены наудачу на одной полке. Найти вероятность того, что четыре определенные книги окажутся поставленными рядом (событие С). Решение. Здесь число равновозможных независимых исходов есть n = P 9=9! Подсчитаем число исходов m, благоприятствующих событию С. Представим себе, что четыре определенные книги связаны вместе, тогда эту связку можно расположить на полке Р 6=6! способами (связка плюс остальные пять книг). Внутри связки четыре книги можно переставлять Р4=4! способами. При этом каждая комбинация внутри связки может сочетаться с каждым из Р 6 способов образования связки, т.е. Следовательно, Пример 11. Сколько можно составить восьмизначных чисел, которые состоят из цифр 2, 3 и 4 при условии что цифры 2 и 3 повторяется по 3 раза, а цифра 4 – 2 раза? Решение. Каждое восьмизначное число будет отличаться от другого порядком следования цифр (в данном случае, Действия над событиями. В процессе решения задач, непосредственный подсчет случаев благоприятствующих данному событию может оказаться очень затруднительным. В связи с этим, для определения вероятности события часто бывает более удобным представление рассматриваемого события в виде комбинации других событий являющихся более простыми. При этом необходимо знать такие правила действий над событиями как сумма, разность и произведение. 1.2.1. Сумма событий Определение: Суммой нескольких событий принято называть событие, которое состоит в наступлении хотя бы одного из них. Так, например, в простейшем случае, когда событий два (А и В ), сумма(А + В) означает такое третье событие С, которое, если они совместны, состоит в появлении либо события А либо В, или того и другого, и наступление либо А либо В, если они несовместны. Теоремы сложения вероятностей: Теорема 1: Вероятность наступления одного из нескольких несовместных событий равна сумме вероятностей этих событий. Отметим, что применение данной теоремы всегда требует проверки рассматриваемых событий на предмет их совместности! Пример 12. В лотерее разыгрывается 1000 билетов, при этом, на один выигрышный билет приходится 100 руб., на 5 билетов – 20 руб., на 100 билетов – 5 руб. Найти вероятность выигрыша не менее 20 рублей по одному лотерейному билету. Решение. Пусть
пусть
пусть
События Пусть
Теорема 2: Вероятность суммы двух совместных событий Пример 13. Найти вероятность, что при подбрасывании двух игральных кубиков хотя бы один раз выпадет 6 очков. Решение. Введем события:
Ввиду того, что события
С учетом того, что
1.2.2 Разность событий Определение: Разностью двух событий Пример 14. Победитель соревнования награждается: призом ( событие Решение. Событие
Примечание: Разность двух событий 1.2.3. Произведение событий Определение: Произведением двух событий Если событий более двух, то их произведением называется событие, которое состоит в совместном появлении всех этих событий. 1.3.Условная вероятность. Теорема умножения вероятностей. Независимые события. Определение: Условной вероятностью Пример 15. В урне содержится три белых и три черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно. Найти вероятность появления белого шара при втором испытании (событие Решение. В урне, после первого испытания осталось 5 шаров, из них 3 белых. Следовательно, искомая условная вероятность
Получим этот же результат можно получить и по формуле (10). Предварительно отметим, что общее число исходов, т. е. совместного появления двух шаров (не важно какого цвета) определяется числом размещений
Теорема: Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что второе событие уже произошло. Уравнение (11) может быть обобщено на случаи любого количества событий. В частности, для трех событий: При этом, совершенно безразлично какое событие считать первым, вторым и. т. д. Т. е., порядок, в котором расположены события, может быть выбран любым. Пример 16. Студент должен сдать по математике зачет и экзамен. Вероятность сдачи зачета равна 0,8. Если зачет сдан, то студент допускается к экзамену, вероятность сдачи которого для студента равна 0,9. Какова вероятность того, что студент сдаст и зачет и экзамен. Решение. Введем следующие события:
Пример 17. Буквы слова "ЗАДАЧА" написаны на отдельных карточках. Наудачу извлекают по одной четыре карточки без возврата. Какова вероятность того, что при этом получится слово "ДАЧА"? Решение: Введем следующие события:
Поскольку, после наступления события
Пример 18. Вероятность попадания в цель каждого из трех орудий соответственно равна Решение. Пусть события
Событие Тогда Искомая вероятность В том случае когда события независимые, например, вероятность события поскольку, в данном случае, условная вероятность события Пример 19.. Имеются 3 ящика, которые содержат по 10 деталей. В первом ящике – 8, во втором – 7, а в третьем – 9 стандартных деталей. Из каждого ящика вынимают наудачу по одной детали. Найти вероятность того, что все три вынутые детали окажутся стандартными. Решение. События
Поскольку события
Пример 20. На обувной фабрике, брак при изготовлении каблука составляет 1%, подметки – 4%, верхней части обуви – 5%. Какова вероятность покупки потребителем хорошей обуви? Решение. Введем следующие события:
Согласно условию задачи:
Тогда
Р(А × В × С) = Р(А) × Р(В) × Р(С) = 0,99 × 0,96 × 0,95 = 0,913. Следовательно, вероятность покупки хорошей обувной пары:
Формула Пуассона. В том случае, если количество испытаний велико Формулы Муавра-Лапласа.. Если количество испытаний велико – локальная – интегральная где Функция Пример 23. Вероятность того, что расход электроэнергии в течение одних суток не превысит установленной нормы, равна 0,75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии: 1) не превысит нормы в течение: а) 4-х суток; б) от 3-х до 4-х суток; 2) превысит норму по крайней мере в течение двух суток. Решение: 1. Введем событие
Ответим на поставленные вопросы задачи: а) число испытаний Событие Используя формулу Бернулли (5), получим:
б) число испытаний
|
|||||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 66; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.147.124 (0.128 с.) |
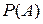 . Предположим, что проводится испытание и из общего количества
. Предположим, что проводится испытание и из общего количества 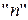 несовместных равновозможных его исходов (случаев),
несовместных равновозможных его исходов (случаев), 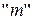 случаев благоприятствуют событию А. Тогда, согласно классическому определению, вероятность события
случаев благоприятствуют событию А. Тогда, согласно классическому определению, вероятность события 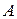 определяется отношением числа исходов ему благоприятствующих, к общему числу исходов:
определяется отношением числа исходов ему благоприятствующих, к общему числу исходов: (1)
(1)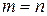 и
и 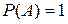 ; если невозможное, то
; если невозможное, то 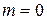 и
и 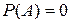 ; если А – случайное событие, то
; если А – случайное событие, то 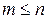 и
и 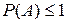 . Следовательно, вполне очевидно что она заключена в пределах:
. Следовательно, вполне очевидно что она заключена в пределах: 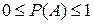 .
.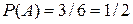 ; событию В – два исхода (выпадение пяти и шести очков), поэтому
; событию В – два исхода (выпадение пяти и шести очков), поэтому 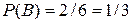 ; событию С – пять исходов (выпадение одного, двух, трех, четырех и пяти очков), следовательно
; событию С – пять исходов (выпадение одного, двух, трех, четырех и пяти очков), следовательно 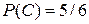 .
.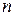 элементов отличаются только порядком расположения этих элементов, то их принято называть перестановками из
элементов отличаются только порядком расположения этих элементов, то их принято называть перестановками из 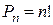 (2)
(2)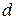 элементов, в котором 1-й элемент повторяется
элементов, в котором 1-й элемент повторяется 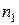 раз, 2-й элемент –
раз, 2-й элемент – 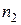 раз, элемент с номером
раз, элемент с номером 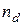 раз и выполняется равенство
раз и выполняется равенство 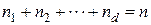 , то такие перестановки принято называть перестановками с повторением из
, то такие перестановки принято называть перестановками с повторением из 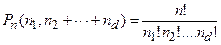 (3)
(3)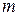 отличаются друг от друга только составом элементов, то их называют сочетанием из
отличаются друг от друга только составом элементов, то их называют сочетанием из 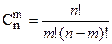 (4)
(4)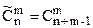 . (5)
. (5)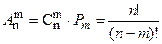 (6)
(6)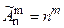 (7)
(7)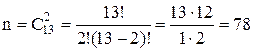
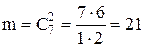 исходов. Следовательно, его вероятность определяется отношением:
исходов. Следовательно, его вероятность определяется отношением: 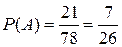 .
.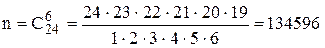 .
.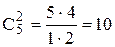 способами, а 4 стандартных детали из 19 стандартных можно выбрать
способами, а 4 стандартных детали из 19 стандартных можно выбрать 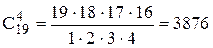 способами. Каждая комбинация бракованных деталей может сочетаться с каждой комбинацией стандартных деталей, поэтому.
способами. Каждая комбинация бракованных деталей может сочетаться с каждой комбинацией стандартных деталей, поэтому. 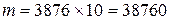 . Следовательно:
. Следовательно:
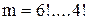 .
.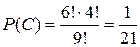 .
.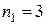 ,
, 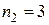 ,
, 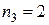 , а их сумма равна 8). Т.е., ответом будет являться перестановка из 8 элементов (см. формулу (3)):
, а их сумма равна 8). Т.е., ответом будет являться перестановка из 8 элементов (см. формулу (3)):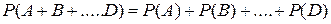 (8)
(8)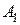 – событие состоящее в выигрыше 5 руб., тогда
– событие состоящее в выигрыше 5 руб., тогда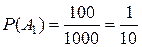 ;
;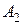 – событие выигрыша 20 руб., тогда
– событие выигрыша 20 руб., тогда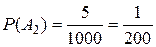
 – событие выигрыша 100 руб., тогда
– событие выигрыша 100 руб., тогда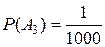
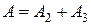 поскольку наступит или
поскольку наступит или 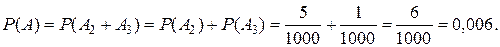
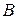 равна сумме вероятностей этих событий без вероятности их совместного появления, то есть
равна сумме вероятностей этих событий без вероятности их совместного появления, то есть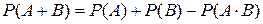 (9)
(9)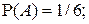
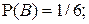
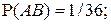 получим:
получим: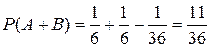 .
.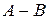 принято называть событие, которое состоится, если
принято называть событие, которое состоится, если 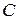 ). Что представляет собой, например, событие
). Что представляет собой, например, событие 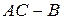 ?
?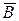 , т.е.:
, т.е.: 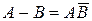 . Соответственно в примере 14 интересующее событие можно представить в виде:
. Соответственно в примере 14 интересующее событие можно представить в виде:  .
.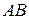 называется такое третье событие, которое состоит в их совместном появлении.
называется такое третье событие, которое состоит в их совместном появлении.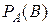 принято называть вероятность события
принято называть вероятность события 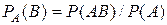 (10)
(10)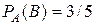
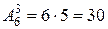 . Из этого числа исходов, событию
. Из этого числа исходов, событию 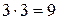 исходов. Поэтому,
исходов. Поэтому, 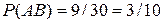 . Искомая условная вероятность
. Искомая условная вероятность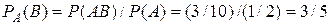
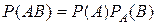 (или,
(или, 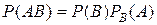 ) (11)
) (11)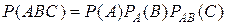 .
.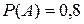 ;
;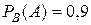 , поскольку событие
, поскольку событие 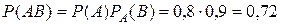 .
.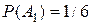 ;
;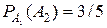 .
.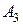 – извлечение буквы "ч", тогда
– извлечение буквы "ч", тогда 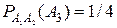 , так как
, так как 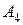 – извлечение буквы "а", тогда
– извлечение буквы "а", тогда 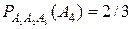 , так как
, так как 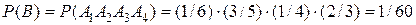 .
.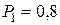 ;
; 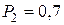 ;
; 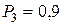 . Найти вероятность хотя бы одного попадания при одном залпе из всех орудий.
. Найти вероятность хотя бы одного попадания при одном залпе из всех орудий.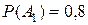 ;
; 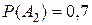 ;
; 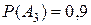 . Тогда события
. Тогда события 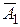 ,
, 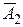 ,
, 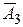 – промахи, соответственно, первого, второго и третьего орудия. Следовательно
– промахи, соответственно, первого, второго и третьего орудия. Следовательно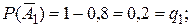

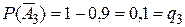 .
.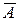 будет состоять в том, что все три орудия промахнутся, т. е.
будет состоять в том, что все три орудия промахнутся, т. е. 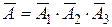 .
.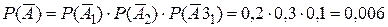
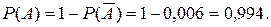
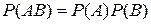 (12)
(12)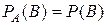 . Равенство (12) можно использовать в качестве определения независимых событий. Два события являются независимыми, если вероятность их совместного наступления равна произведению вероятностей этих событий. Если
. Равенство (12) можно использовать в качестве определения независимых событий. Два события являются независимыми, если вероятность их совместного наступления равна произведению вероятностей этих событий. Если 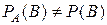 – события
– события 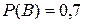 ;
; 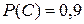 .
.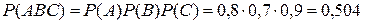 .
.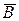 – выпуск бракованной подметки;
– выпуск бракованной подметки;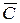 – выпуск бракованного верха.
– выпуск бракованного верха.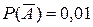 ;
; 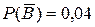 ;
; 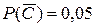
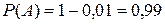 ;
; 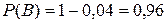 ;
; 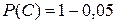 ;
;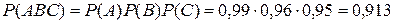 .
.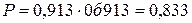 .
.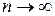 , а вероятность события мала
, а вероятность события мала 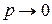 , так что
, так что 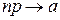 ,
, 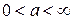 и
и 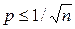 . то используется приближенная формула Пуассона:
. то используется приближенная формула Пуассона: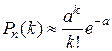 (17)
(17)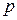 и
и 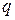 достаточно большие, так что выполняются условия;
достаточно большие, так что выполняются условия; 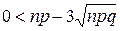 и
и 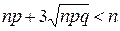 , то применяют следующие приближенные формулы Муавра-Лапласа:
, то применяют следующие приближенные формулы Муавра-Лапласа: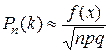 где;
где; 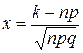 ;
; 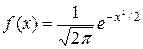 – функция Гаусса.
– функция Гаусса.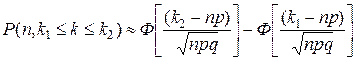
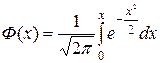 – функция Лапласа.
– функция Лапласа.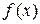 – четная (
– четная (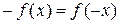 , а
, а 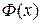 – нечетная (
– нечетная (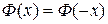 ) Обе функции табулированы (см. Приложение).
) Обе функции табулированы (см. Приложение).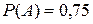 . Тогда событие
. Тогда событие 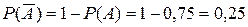 .
.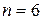
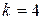 ,
, 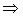
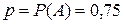 ;
;