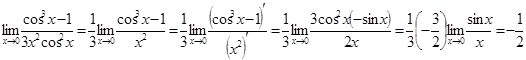Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление пределов (Правило Лопиталя) ⇐ ПредыдущаяСтр 4 из 4
Рассмотрим вычисление пределов дроби Теорема 6. Пусть функции f и g дифференцируемы в некоторой проколотой окрестности U точки a (т.е дифференцируемы во всех точках этой окрестности, за исключением, быть может, самой точки a), g ’(x) отлично от нуля в U, и пусть
в случае, когда Доказательство. Доопределим функции f и g, положив их значение в точке a равным нулю, f (a)= g (a)=0, то
где точка c лежит между a и x. При
что и требовалось доказать. [2, c. 135] Замечание. Условие теоремы 1 выполнены, если функции f и g дифференцируемы в проколотой окрестности точки a, непрерывны в этой точке, причем f (a)= g (a)=0. Теорема 7. Пусть функции f и g дифференцируемы на луче
Доказательство. Положим х =
Имеем
Для вычисления предела
Теорема доказана. [2, c. 135] В этих теоремах мы рассмотрели случаи раскрытия неопределенности вида Теперь мы рассмотрим вопрос о раскрытие неопределенности вида Теорема 8. Пусть функции f и g дифференцируемы на луче
Доказательство. Возьмем произвольное положительное число ε>0. по условию существует
Не ограничивая общности рассуждений, мы можем считать, что
Так как
откуда
Перепишем это неравенство в виде
где для краткости через Так как Разделим обе части неравенства (22’) на
Итак, для любого ε>0 существует число М, такое, что для
Замечание. Теорема сохраняет свою силу и в случае, когда
В этом случае
Замечание. Теорема справедлива и в случае Теоремы 6, 7, 8 называются правилом Лопиталя. Рассмотрим примеры применения правила Лопиталя для вычисления пределов функций. Пример 21. Вычислим
Решение. Здесь имеем неопределенность вида
Разумеется, используя и в дальнейшем подобную краткую запись, мы предполагаем, что все условия соответствующей данному случаю теоремы выполнены и, в частности, что предел отношения производных существует. Пример 22. Вычислим
а при
Но тогда, в силу того, что функция
Иногда при вычисление пределов с помощью правила Лопиталя получается, что Пример 23. Вычислим
Решение. Имеем неопределенность вида
Снова получилась неопределенность вида
Итак,
Во многих случаях дифференцирование, которое мы применяем по правилу Лопиталя, приводит к более простым выражениям, если предварительно заменить бесконечно малую эквивалентной бесконечно малой или выполнить необходимые упрощения. Пример 24. Вычислим
Решение. Так как
Имеем неопределенность вида
Снова имеем неопределенность вида
Заключение Изучив материал в количестве 10 источников были решены и поставлены задачи исследования и достигнута цель работы. В представленной работе материал структурирован. Общий объем работы 40 страниц. Работа содержит две главы, в первой главе «Понятия необходимые для решения математических задач с помощью производной» даны понятия производной, предела функции, интеграла, дифференциала функции. Во второй главе «Применение производной к решению задач» описано исследование функции, применение производной при решении задач в разных науках, таких как геометрия, физика, вычисление интегралов, доказательство неравенств, вычисление пределов (правило Лапиталя). Было решено 24 примера, из них самостоятельно составлено 5 примеров. Работа по данной теме способствовала формированию поисковых и исследовательских навыков, развитию логического и конструктивного мышления. Работа по данной теме интересна, и поэтому будет продолжено ее исследование в методическом аспекте.
Список литературы
1.Алимов Ш.А. алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. / Ш.А. Алимов, Ю.В. Сидоров и др.- М.: Просвещение, 1992.- 254 с. .Виленкин Н.Я. Математический анализ: Дифференц. исчисление. Учебн. пособие для студентов-заочников I курс физ.-мат. фак. пед. ин-тов / Н.Я. Виленкин, А.Г. Мордкович, Е.С. Куницкая.- 2-е изд., перераб.- М.: Просвещение, 1984.- 175 с. .Гусев В.А. Математика: Справ. Материал: Кн. для учащихся. / В.А. Гусев, А.Г. Мордкович.- М.: Просвещение, 1988.-416 с. .Колмогоров А.Н. алгебра и начала анализа. Учеб. для 10-11 кл. сред. шк. / А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын и др.: Под ред. А.Н. Колмогорова. - 2-е изд.- М.: Просвещение, 1991.-320 с. . Пискунов Н.С. Дифференциальное и интегральное исчисление: Учеб. для вузов. В 2-х т. Т. 1. / Н.С. Пискунов.- М.: Интеграл-Пресс, 2002.-416 с. .Рубинов А.М. элементы математического анализа: Учеб. пособие для учителей / А.М. Рубинов, К.Ш. Шапиев.- М.: Просвещение, 1972.-278 сШефель В.Г. Высшая математика. Учебн. пособие для студентов-заочников / В.Г. Шефель, М.В. Грунина, В.Н. Бабин,.- Новосибирск, 2001.-253 с. .Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления: В 3 т. Т. 1 / Г. М. Фихтенгольц; пред и прим А.А. Флоринского.- М.: ФИЗМАТЛИТ, Лаборатория Знаний, 2003.-680 с. .Жафяров А.Ж. Геометрия: Учеб. пособие: В 2-х ч. Ч. 2.-2-е изд., адаптированное под стандарты II поколения.- Новосибирск: Сиб. унив. Изд-во, 2003.-267 с. .Жафяров А.Ж. Геометрия: Учеб. пособие: В 2-х ч. Ч. 1.-2-е изд., адаптированное под стандарты II поколения.- Новосибирск: Сиб. унив. Изд-во, 2002.-271 с.
|
||||||
|
Последнее изменение этой страницы: 2021-04-20; просмотров: 63; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.105.255 (0.052 с.) |
 , когда x
, когда x 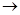 a или x
a или x 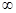 , причем f (x) и g (x) либо одновременно стремятся к нулю, либо одновременно стремятся к бесконечности.
, причем f (x) и g (x) либо одновременно стремятся к нулю, либо одновременно стремятся к бесконечности.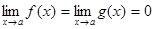 . Тогда если существует
. Тогда если существует 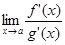 , то существует и
, то существует и 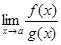 , причем эти пределы равны:
, причем эти пределы равны: =
=  .
. и
и 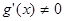 , геометрический смысл этой теоремы состоит в следующем. Графики функций
, геометрический смысл этой теоремы состоит в следующем. Графики функций 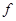 и
и 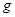 пересекают ось абсцисс в точке М(a;0), и поэтому уравнения их касательных к этим графикам в точке М имеют вид
пересекают ось абсцисс в точке М(a;0), и поэтому уравнения их касательных к этим графикам в точке М имеют вид  и
и 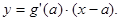 Но предел отношения функций
Но предел отношения функций 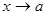 равен пределу отношения ординат касательных при
равен пределу отношения ординат касательных при 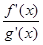 .
. ,
,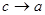 и поэтому
и поэтому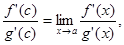

 , причем
, причем  . Если существует
. Если существует  , то существует и
, то существует и  :
: .Тогда
.Тогда ,
, 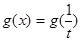 ,
, ,
, 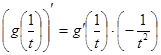 .
. .
.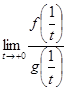 воспользуемся теоремой 1. Получим
воспользуемся теоремой 1. Получим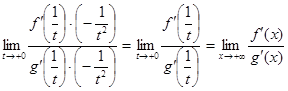 .
.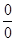 , когда
, когда 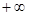 или
или 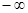 , где a - число или один из символов
, где a - число или один из символов 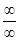 . Начнем со случая, когда x
. Начнем со случая, когда x 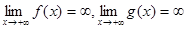 .Тогда если существует
.Тогда если существует  =А. Тогда по определению предела найдется такое число N, что для
=А. Тогда по определению предела найдется такое число N, что для  выполняется неравенство
выполняется неравенство . (21)
. (21)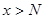 . Применив к отрезку
. Применив к отрезку 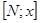 теорему Коши, получим
теорему Коши, получим где
где 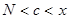 .
.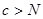 , то, воспользовавшись неравенством (21), получим
, то, воспользовавшись неравенством (21), получим ,
,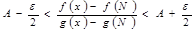 . (22)
. (22)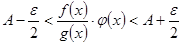 , (22’)
, (22’)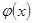 обозначена дробь
обозначена дробь  .
. , то
, то 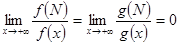 и поэтому
и поэтому 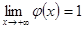 .
.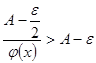 и
и  , а поэтому
, а поэтому . (23)
. (23) выполняется неравенство (23), а это означает, что
выполняется неравенство (23), а это означает, что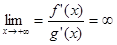 .
.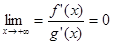 , а тогда и
, а тогда и 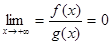 . Отсюда следует, что
. Отсюда следует, что 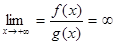 , т. е.
, т. е.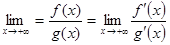 .
.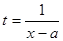 . Если
. Если  и теорема сводится к уже доказанной.
и теорема сводится к уже доказанной. .
.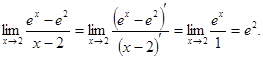
 ,
,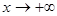 знаменатель
знаменатель  , в нуль. Поэтому поступим иначе. Сначала с помощью правила Лопиталя найдем предел
, в нуль. Поэтому поступим иначе. Сначала с помощью правила Лопиталя найдем предел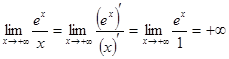 .
.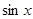 ограничена и потому
ограничена и потому 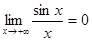 , получаем
, получаем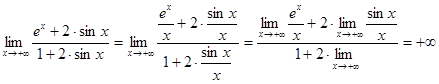 .
.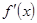 и
и 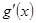 отношением их производных, т. е. выражением
отношением их производных, т. е. выражением 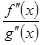 .
. .
.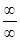 . Воспользуемся правилом Лопиталя:
. Воспользуемся правилом Лопиталя: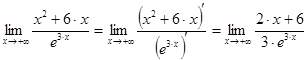 .
.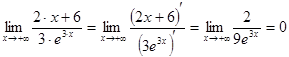 .
.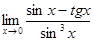 .
.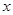 при
при 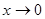 , то
, то  ~
~ 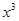 и, следовательно,
и, следовательно, .
. .
. . Получим
. Получим